Введение
Для системы с явными потерями датский математик А. К. Erlang получил следующее выражение:
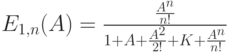
где А - поток нагрузки, выраженный в Эрлангах.
Эта формула часто используется при оценке числа устройств для обслуживания нагрузки. Она применяется не только для групп с полной доступностью, но также как инструмент для оценки нагрузки в группах с ограниченной доступностью. Отношение между числом устройств  , нагрузкой и величиной
, нагрузкой и величиной  довольно сложно, поэтому для расчетов применяются таблицы.
довольно сложно, поэтому для расчетов применяются таблицы.
Предлагаемые таблицы состоят из двух частей. Часть I дает значения  как функции
как функции  и
и  , где
, где  принимает 20 дискретных значений между 0, 00001 и 0,4 и
принимает 20 дискретных значений между 0, 00001 и 0,4 и  . Часть II дает значения
. Часть II дает значения  как функция
как функция  и
и  , где
, где  и
и  .
.
Методы, используемые в таблице, дают высокую точность вычисленных значений.
Значения  нагрузки частично приводятся с 5 рисунками. Значения
нагрузки частично приводятся с 5 рисунками. Значения  перегрузки (^4) в части II даются как числа с 6 десятичными знаками. Значения округлены, согласно обычным правилам.
перегрузки (^4) в части II даются как числа с 6 десятичными знаками. Значения округлены, согласно обычным правилам.
Обе части таблицы сопровождаются пояснениями и двумя числовыми примерами.
Часть I. Таблица А для заданных Ei ,n (А) и п
Таблица для данных значений  и
и 
В этой части поток предложенной нагрузки сведен в таблицу для данных значений вероятности потери  , и число из устройств
, и число из устройств  .
.
Вероятность потери Е имеет следующие постоянные значения:
0,00001, 0,00005, 0,0001, 0,0005, 0,001, 0,002, 0,003, 0..004, 0..005, 0,006, 0,007, 0,008, 0,009, 0,01, 0,02, 0,03, 0,05, 0,1, 0.2, и 0,4.
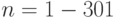
Пример
Найдите требуемое число устройств  для
для  Эрл и вероятность потери
Эрл и вероятность потери 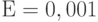 .
.
На стр.5 и в столбце для 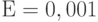 можно заметить, что
можно заметить, что  соответствует значение
соответствует значение  Эрл а
Эрл а  - значение
- значение  . Следовательно, требуемое число устройств - 83.
. Следовательно, требуемое число устройств - 83.
Offered traffic flow A in erlang n=1-51
| n |
Loss probability (E) |
n |
|
0.00001 |
0.00005 |
0.0001 |
0.0005 |
0.001 |
0.002 |
0.003 |
0.004 |
0.005 |
0.006 |
|
| 1 |
.0001 |
.00005 |
.00010 |
.00050 |
.00100 |
.00200 |
.00301 |
.00402 |
.00503 |
.00604 |
1 |
| 2 |
.00448 |
.01005 |
.01425 |
.03213 |
.04576 |
.06534 |
.08064 |
.09373 |
.10540 |
.11608 |
2 |
| 3 |
.03980 |
.06849 |
.08683 |
.15170 |
.19384 |
.24872 |
.28851 |
.32099 |
.34900 |
.37395 |
3 |
| 4 |
.12855 |
.19554 |
.23471 |
.36236 |
.43927 |
.53503 |
.60209 |
.65568 |
.70120 |
.74124 |
4 |
| 5 |
.27584 |
.38851 |
.45195 |
.64857 |
.76212 |
.89986 |
.99446 |
1.0692 |
1.1320 |
1.1870 |
5 |
| 6 |
.47596 |
.63923 |
.72826 |
.99567 |
1.1459 |
1.3252 |
1.4468 |
1.5421 |
1.6218 |
1.6912 |
6 |
| 7 |
.72378 |
.93919 |
1.0541 |
1.3922 |
1.5786 |
1.7984 |
1.9463 |
2.0614 |
2.1575 |
2.2408 |
7 |
| 8 |
1.0133 |
1.2816 |
1.4219 |
1.8298 |
2.0513 |
2.3106 |
2.4837 |
2.6181 |
2.7299 |
2.8266 |
8 |
| 9 |
1.3391 |
1.6595 |
1.8256 |
2.3016 |
2.5575 |
2.8549 |
3.0526 |
3.2057 |
3.3326 |
3.4422 |
9 |
| 10 |
1.6970 |
2.0689 |
2.2601 |
2.8028 |
3.0920 |
3.4265 |
3.6480 |
3.8190 |
3.9607 |
4.0829 |
10 |
| 11 |
2.0849 |
2.5059 |
2.7216 |
3.3294 |
3.6511 |
4.0215 |
4.2661 |
4.4545 |
4.6104 |
4.7447 |
11 |
| 12 |
2.4958 |
2.9671 |
3.2072 |
3.8781 |
4.2314 |
4.6368 |
4.9038 |
5.1092 |
5.2789 |
5.4250 |
12 |
| 13 |
2.9294 |
3.4500 |
3.7136 |
4.4465 |
4.8306 |
5.2700 |
5.5588 |
5.7807 |
5.9638 |
6.1214 |
13 |
| 14 |
3.3834 |
3.9523 |
4.2388 |
5.0324 |
5.4464 |
5.9190 |
6.2291 |
6.4670 |
6.6632 |
6.8320 |
14 |
| 15 |
3.8559 |
4.4721 |
4.7812 |
5.6339 |
6.0772 |
6.5822 |
6.9130 |
7.1665 |
7.3755 |
7.5552 |
15 |
| 16 |
4.3453 |
5.0079 |
5.3390 |
6.2496 |
6.7215 |
7.2582 |
7.6091 |
7.8780 |
8.0995 |
8.2898 |
16 |
| 17 |
4.8502 |
5.5583 |
5.9110 |
6.8782 |
7.3781 |
7.9457 |
8.3164 |
8.6003 |
8.8340 |
9.0347 |
17 |
| 18 |
5.3693 |
6.1220 |
6.4959 |
7.5186 |
8.0459 |
8.6437 |
9.0339 |
9.3324 |
9.5780 |
9.7889 |
18 |
| 19 |
5.9016 |
6.6980 |
7.0927 |
8.1698 |
8.7239 |
9.3515 |
9.7606 |
10.073 |
10.331 |
10.552 |
19 |
| 20 |
6.4460 |
7.2854 |
7.7005 |
8.8310 |
9.4115 |
10.068 |
10.496 |
10.823 |
11.092 |
11.322 |
20 |
| 21 |
7.0017 |
7.8834 |
8.3186 |
9.5014 |
10.108 |
10.793 |
11.239 |
11.580 |
11.860 |
12.100 |
21 |
| 22 |
7.5680 |
8.4926 |
8.9462 |
10.180 |
10.812 |
11.525 |
11.989 |
12.344 |
12.635 |
12.885 |
22 |
| 23 |
8.1443 |
9.1095 |
9.5826 |
10.868 |
11.524 |
12.265 |
12.746 |
13.114 |
13.416 |
13.676 |
23 |
| 24 |
8.7298 |
9.7351 |
10.227 |
11.562 |
12.243 |
13.011 |
13.510 |
13.891 |
14.204 |
14.472 |
24 |
| 25 |
9.3240 |
10.369 |
10.880 |
12.264 |
12.969 |
13.763 |
14.279 |
14.673 |
14.997 |
15.274 |
25 |
| 26 |
9.9265 |
11.010 |
11.540 |
12.972 |
13.701 |
14.522 |
15.054 |
15.461 |
15.795 |
16.081 |
26 |
| 27 |
10.537 |
11.659 |
12.207 |
13.686 |
14.439 |
15.285 |
15.835 |
16.254 |
16.598 |
16.893 |
27 |
| 28 |
11.154 |
12.314 |
12.880 |
14.406 |
15.182 |
16.054 |
16.620 |
17.051 |
17.406 |
17.709 |
28 |
| 29 |
11.779 |
12.976 |
13.560 |
15.132 |
15.930 |
16.828 |
17.410 |
17.853 |
18.218 |
18.530 |
29 |
| 30 |
12.417 |
13.644 |
14.246 |
15.863 |
16.684 |
17.606 |
18.204 |
18.660 |
19.034 |
19.355 |
30 |
| 31 |
13.054 |
14.318 |
14.937 |
16.599 |
17.442 |
18.389 |
19.002 |
19.470 |
19.854 |
20.183 |
31 |
| 32 |
13.697 |
14.998 |
15.633 |
17.340 |
18.205 |
19.176 |
19.805 |
20.284 |
20.678 |
21.015 |
32 |
| 33 |
14.346 |
15.682 |
16.335 |
18.085 |
18.972 |
19.966 |
20.611 |
21.102 |
21.505 |
21.850 |
33 |
| 34 |
15.001 |
16.372 |
17.041 |
18.835 |
19.743 |
20.761 |
21.421 |
21.923 |
22.336 |
22.689 |
34 |
| 35 |
15.660 |
17.067 |
17.752 |
19.589 |
20.517 |
21.559 |
22.234 |
22.748 |
23.169 |
23.531 |
35 |
| 36 |
16.325 |
17.766 |
18.468 |
20.347 |
21.296 |
22.361 |
23.050 |
23.575 |
24.006 |
24.376 |
36 |
| 37 |
16.995 |
18.470 |
19.188 |
21.108 |
22.078 |
23.166 |
23.870 |
24.406 |
24.846 |
25.223 |
37 |
| 38 |
17.669 |
19.178 |
19.911 |
21.873 |
22.864 |
23.974 |
24.692 |
25.240 |
25.689 |
26.074 |
38 |
| 39 |
18.348 |
19.890 |
20.640 |
22.642 |
23.652 |
24.785 |
25.518 |
26.076 |
26.534 |
26.926 |
39 |
| 40 |
19.031 |
20.606 |
21.372 |
23.414 |
24.444 |
25.599 |
26.346 |
26.915 |
27.382 |
27.782 |
40 |
| 41 |
19.718 |
21.326 |
22.107 |
24.189 |
25.239 |
26.416 |
27.177 |
27.756 |
28.232 |
28.640 |
41 |
| 42 |
20.409 |
22.049 |
22.846 |
24.967 |
26.037 |
27.235 |
28.010 |
28.600 |
29.085 |
29.500 |
42 |
| 43 |
21.104 |
22.776 |
23.587 |
25.748 |
26.837 |
28.057 |
28.846 |
29.447 |
29.940 |
30.362 |
43 |
| 44 |
21.803 |
23.507 |
24.333 |
26.532 |
27.641 |
28.882 |
29.684 |
30.295 |
30.797 |
31.227 |
44 |
| 45 |
22.505 |
24.240 |
25.081 |
27.319 |
28.447 |
29.708 |
30.525 |
31.146 |
31.656 |
32.093 |
45 |
| 46 |
23.211 |
24.977 |
25.833 |
28.109 |
29.255 |
30.538 |
31.367 |
31.999 |
32.517 |
32.962 |
46 |
| 47 |
23.921 |
25.717 |
26.587 |
28.901 |
30.066 |
31.369 |
32.212 |
32.854 |
33.381 |
33.832 |
47 |
| 48 |
24.633 |
26.460 |
27.344 |
29.696 |
30.879 |
32.203 |
33.059 |
33.711 |
34.246 |
34.704 |
48 |
| 49 |
25.349 |
27.206 |
28.104 |
30.493 |
31.694 |
33.039 |
33.908 |
34.570 |
35.113 |
35.578 |
49 |
| 50 |
26.067 |
27.954 |
28.867 |
31.292 |
32.512 |
33.876 |
34.759 |
35.431 |
35.982 |
36.454 |
50 |
| 51 |
26.789 |
28.706 |
29.632 |
32.094 |
33.332 |
34.716 |
35.611 |
36.293 |
36.852 |
37.331 |
51 |
|
0.00001 |
0.00005 |
0.0001 |
0.0005 |
0.001 |
0.002 |
0.003 |
0.004 |
0.005 |
0.006 |
|
| n |
Loss probability (E) |
n |
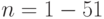
Offered traffic flow A in erlang
| n |
Loss probability (E) |
n |
|
0.007 |
0.008 |
0.009 |
0.01 |
0.02 |
0.03 |
0.05 |
0.1 |
0.2 |
0.4 |
|
| 1 |
.00705 |
.00806 |
.00908 |
.01010 |
.02041 |
.03093 |
.05263 |
.11111 |
.25000 |
.66667 |
1 |
| 2 |
.12600 |
.13532 |
.14416 |
.15259 |
.22347 |
.28155 |
.38132 |
.59543 |
1.0000 |
2.0000 |
2 |
| 3 |
.39664 |
.41757 |
.43711 |
.45549 |
.60221 |
.71513 |
.89940 |
1.2708 |
1.9299 |
3.4798 |
3 |
| 4 |
.77729 |
.81029 |
.84085 |
.86942 |
1.0923 |
1.2589 |
1.5246 |
2.0454 |
2.9452 |
5.0210 |
4 |
| 5 |
1.2362 |
1.2810 |
1.3223 |
1.3608 |
1.6571 |
1.8752 |
2.2185 |
2.8811 |
4.0104 |
6.5955 |
5 |
| 6 |
1.7531 |
1.8093 |
1.8610 |
1.9090 |
2.2759 |
2.5431 |
2.9603 |
3.7584 |
5.1086 |
8.1907 |
6 |
| 7 |
2.3149 |
2.3820 |
2.4437 |
2.5009 |
2.9354 |
3.2497 |
3.7378 |
4.6662 |
6.2302 |
9.7998 |
7 |
| 8 |
2.9125 |
2.9902 |
3.0615 |
3.1276 |
3.6271 |
3.9865 |
4.5430 |
5.5971 |
7.3692 |
11.419 |
8 |
| 9 |
3.5395 |
3.6274 |
3.7080 |
3.7825 |
4.3447 |
4.7479 |
5.3702 |
6.5464 |
8.5217 |
13.045 |
9 |
| 10 |
4.1911 |
4.2889 |
4.3784 |
4.4612 |
5.0840 |
5.5294 |
6.2157 |
7.5106 |
9.6850 |
14.677 |
10 |
| 11 |
4.8637 |
4.9709 |
5.0691 |
5.1599 |
5.8415 |
6.3280 |
7.0764 |
8.4871 |
10.857 |
16.314 |
11 |
| 12 |
5.5543 |
5.6708 |
5.7774 |
5.8760 |
6.6147 |
7.1410 |
7.9501 |
9.4740 |
12.036 |
17.954 |
12 |
| 13 |
6.2607 |
6.3863 |
6.5011 |
6.6072 |
7.4015 |
7.9667 |
8.8349 |
10.470 |
13.222 |
19.598 |
13 |
| 14 |
6.9811 |
7.1155 |
7.2382 |
7.3517 |
8.2003 |
8.8035 |
9.7295 |
11.473 |
14.413 |
21.243 |
14 |
| 15 |
7.7139 |
7.8568 |
7.9874 |
8.1080 |
9.0096 |
9.6500 |
10.633 |
12.484 |
15.608 |
22.891 |
15 |
| 16 |
8.4579 |
8.6092 |
8.7474 |
8.8750 |
9.8284 |
10.505 |
11.544 |
13.500 |
16.807 |
24.541 |
16 |
| 17 |
9.2119 |
9.3714 |
9.5171 |
9.6516 |
10.656 |
11.368 |
12.461 |
14.522 |
18.010 |
26.192 |
17 |
| 18 |
9.9751 |
10.143 |
10.296 |
10.437 |
11.491 |
12.238 |
13.385 |
15.548 |
19.216 |
27.844 |
18 |
| 19 |
10.747 |
10.922 |
11.082 |
11.230 |
12.333 |
13.115 |
14.315 |
16.579 |
20.424 |
29.498 |
19 |
| 20 |
11.526 |
11.709 |
11.876 |
12.031 |
13.182 |
13.997 |
15.249 |
17.613 |
21.635 |
31.152 |
20 |
| 21 |
12.312 |
12.503 |
12.677 |
12.838 |
14.036 |
14.885 |
16.189 |
18.651 |
22.848 |
32.808 |
21 |
| 22 |
13.105 |
13.303 |
13.484 |
13.651 |
14.896 |
15.778 |
17.132 |
19.692 |
24.064 |
34.464 |
22 |
| 23 |
13.904 |
14.110 |
14.297 |
14.470 |
15.761 |
16.675 |
18.080 |
20.737 |
25.281 |
36.121 |
23 |
| 24 |
14.709 |
14.922 |
15.116 |
15.295 |
16.631 |
17.577 |
19.031 |
21.784 |
26.499 |
37.779 |
24 |
| 25 |
15.519 |
15.739 |
15.939 |
16.125 |
17.505 |
18.483 |
19.985 |
22.833 |
27.720 |
39.437 |
25 |
| 26 |
16.334 |
16.561 |
16.768 |
16.959 |
18.383 |
19.392 |
20.943 |
23.885 |
28.941 |
41.096 |
26 |
| 27 |
17.153 |
17.387 |
17.601 |
17.797 |
19.265 |
20.305 |
21.904 |
24.939 |
30.164 |
42.755 |
27 |
| 28 |
17.977 |
18.218 |
18.438 |
18.640 |
20.150 |
21.221 |
22.867 |
25.995 |
31.388 |
44.414 |
28 |
| 29 |
18.805 |
19.053 |
19.279 |
19.487 |
21.039 |
22.140 |
23.833 |
27.053 |
32.614 |
46.074 |
29 |
| 30 |
19.637 |
19.891 |
20.123 |
20.337 |
21.932 |
23.062 |
24.802 |
28.113 |
33.840 |
47.735 |
30 |
| 31 |
20.473 |
20.734 |
20.972 |
21.191 |
22.827 |
23.987 |
25.773 |
29.174 |
35.067 |
49.395 |
31 |
| 32 |
21.312 |
21.580 |
21.823 |
22.048 |
23.725 |
24.914 |
26.746 |
30.237 |
36.295 |
51.056 |
32 |
| 33 |
22.155 |
22.429 |
22.678 |
22.909 |
24.626 |
25.844 |
27.721 |
31.301 |
37.524 |
52.718 |
33 |
| 34 |
23.001 |
23.281 |
23.536 |
23.772 |
25.529 |
26.776 |
28.698 |
32.367 |
38.754 |
54.379 |
34 |
| 35 |
23.849 |
24.136 |
24.397 |
24.638 |
26.435 |
27.711 |
29.677 |
33.434 |
39.985 |
56.041 |
35 |
| 36 |
24.701 |
24.994 |
25.261 |
25.507 |
27.343 |
28.647 |
30.657 |
34.503 |
41.216 |
57.703 |
36 |
| 37 |
25.556 |
25.854 |
26.127 |
26.378 |
28.254 |
29.585 |
31.640 |
35.572 |
42.448 |
59.365 |
37 |
| 38 |
26.413 |
26.718 |
26.996 |
27.252 |
29.166 |
30.526 |
32.624 |
36.643 |
43.680 |
61.028 |
38 |
| 39 |
27.272 |
27.583 |
27.867 |
28.129 |
30.081 |
31.468 |
33.609 |
37.715 |
44.913 |
62.690 |
39 |
| 40 |
28.134 |
28.451 |
28.741 |
29.007 |
30.997 |
32.412 |
34.596 |
38.787 |
46.147 |
64.353 |
40 |
| 41 |
28.999 |
29.322 |
29.616 |
29.888 |
31.916 |
33.357 |
35.584 |
39.861 |
47.381 |
66.016 |
41 |
| 42 |
29.866 |
30.194 |
30.494 |
30.771 |
32.836 |
34.305 |
36.574 |
40.936 |
48.616 |
67.679 |
42 |
| 43 |
30.734 |
31.069 |
31.374 |
31.656 |
33.758 |
35.253 |
37.565 |
42.011 |
49.851 |
69.342 |
43 |
| 44 |
31.605 |
31.946 |
32.256 |
32.543 |
34.682 |
36.203 |
38.557 |
43.088 |
51.086 |
71.006 |
44 |
| 45 |
32.478 |
32.824 |
33.140 |
33.432 |
35.607 |
37.155 |
39.550 |
44.165 |
52.322 |
72.669 |
45 |
| 46 |
33.353 |
33.705 |
34.026 |
34.322 |
36.534 |
38.108 |
40.545 |
45.243 |
53.559 |
74.333 |
46 |
| 47 |
34.230 |
34.587 |
34.913 |
35.215 |
37.462 |
39.062 |
41.540 |
46.322 |
54.796 |
75.997 |
47 |
| 48 |
35.108 |
35.471 |
35.803 |
36.109 |
38.392 |
40.018 |
42.537 |
47.401 |
56.033 |
77.660 |
48 |
| 49 |
35.988 |
36.357 |
36.694 |
37.004 |
39.323 |
40.975 |
43.534 |
48.481 |
57.270 |
79.324 |
49 |
| 50 |
36.870 |
37.245 |
37.586 |
37.901 |
40.255 |
41.933 |
44.533 |
49.562 |
58.508 |
80.988 |
50 |
| 51 |
37.754 |
38.134 |
38.480 |
38.800 |
41.189 |
42.892 |
45.533 |
50.644 |
59.746 |
82.652 |
51 |
|
0.007 |
0.008 |
0.009 |
0.01 |
0.02 |
0.03 |
0.05 |
0.1 |
0.2 |
0.4 |
|
|
Loss probability (E) |
|
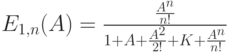
 , нагрузкой и величиной
, нагрузкой и величиной  довольно сложно, поэтому для расчетов применяются таблицы.
довольно сложно, поэтому для расчетов применяются таблицы. как функции
как функции  и
и  , где
, где  принимает 20 дискретных значений между 0, 00001 и 0,4 и
принимает 20 дискретных значений между 0, 00001 и 0,4 и  . Часть II дает значения
. Часть II дает значения  как функция
как функция  и
и  , где
, где  и
и  .
. нагрузки частично приводятся с 5 рисунками. Значения
нагрузки частично приводятся с 5 рисунками. Значения  перегрузки (^4) в части II даются как числа с 6 десятичными знаками. Значения округлены, согласно обычным правилам.
перегрузки (^4) в части II даются как числа с 6 десятичными знаками. Значения округлены, согласно обычным правилам. , и число из устройств
, и число из устройств  .
.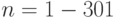
 для
для  Эрл и вероятность потери
Эрл и вероятность потери 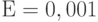 .
.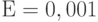 можно заметить, что
можно заметить, что  соответствует значение
соответствует значение  Эрл а
Эрл а  - значение
- значение  . Следовательно, требуемое число устройств - 83.
. Следовательно, требуемое число устройств - 83.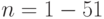

 и
и