|
Хочу получить удостоверение. Сколько стоит оплата? |
Инспектор
Вы можете этот курс.
Опубликован: 10.12.2015 | Доступ: платный | Студентов: 23 / 7 | Длительность: 07:10:00
Тема: Программирование
Специальности: Программист, Системный архитектор
Лекция 11:
Определение функций
< Лекция 10 || Лекция 11 || Лекция 12 >
Ключевые слова: программа, имя функции, определение функции, функция, void, идентификатор, список, сигнатура, double, int, фигурные скобки, значение, return, определение, прототип функции, вызов функции, выражение, вещественное число, аппроксимация, Размещение, область видимости, локальная переменная, глобальная область видимости
Каждая программа на языке С++ - представляет собой совокупность функций, каждая из которых должна быть определена до ее использования. В определении функции указывается последовательность действий, выполняемых при ее вызове, имя функции, тип функции (тип возвращаемого функцией значения, т.е. тип результата) и совокупность формальных параметров (аргументов).
Определение функции имеет следующий вид:
тип_функции имя_функции (спецификация_формальных_параметров)
{
тело_функции
}
Тип_функции – тип возвращаемого функцией значения, если функция не возвращает никакого значения используется тип void. Имя_функции – уникальный идентификатор, спецификация_формальных_параметров – это либо пусто, либо void, либо список спецификаций отдельных параметров. Спецификация формальных параметров иначе еще называется "сигнатура функции". Спецификация каждого отдельного параметра имеет вид:
тип имя_параметра тип имя_параметра = значение_по_умолчанию
Тело_функции – это последовательность описаний и операторов, заключенных в фигурные скобки. Возвращаемое функцией значение определяется оператором return. Если функция не возвращает никакого значения, т.е. имеет тип void, то оператор return опускается.
Перед первым использованием функции требуется поместить ее определение или описание (прототип), содержащее тип возвращаемых функцией значений и тип параметров. Прототип функции почти совпадает с ее заголовком, отличие в том, что после него ставится точка с запятой. В спецификации формальных параметров прототипа могут опускаться имена переменных.
Обращение к функции (вызов функции) – это выражение, в которое подставляется список фактических параметров:
Имя функции (список фактических параметров)
Значением выражения "вызов функции" является возвращаемое функцией значение, тип которого соответствует типу функции. Соответствие между формальными и фактическими параметрами устанавливается по их взаимному расположению в списках. Приведем несколько примеров использования функций.
В приводимом ниже примере функция Furier() не возвращает значений, она всего лишь выдает значение на экран, ее параметром является вещественное число двойной точности.
//==========================================================
// Name : furier.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
//Эти директивы препроцессора определяют максимальный
//размер массива
#define array_size 6
void Furier(double x)
{
//Вычислим число Пи
double pi=4*atan(1);
double f; //Значение функции, апроксимирующей ряд Фурье
f=0;
for(int i=1;i<array_size;i++)
{
f+=pow((2/(i*pi)),2)*(cos(i*pi)-1)*cos((i*pi*x)/2);
cout<<"\nf["<<i<<"] = "<<f+1;
}
cout<<"\n"<<endl;
}
int main() {
//Прототип функции
void Furier(double x);
//Координаты точки x
double x;
cout<<"\nInput x coordinate ";
cin>>x;
//Вызов функции по значению
Furier(x);
return 0;
}
Результат:
Input x coordinat 1.85 f[1]=1.78817 f[2]=1.78817 f[3]=1.85666 f[4]=1.85666 f[5]=1.86907
Ряды Фурье часто используются при решении дифференциальных уравнений и для описания периодических функций. Ряды Фурье - это бесконечные ряды, представляющие собой сумму тригонометрических функций, период которых монотонно убывает.
Ряд Фурье по синусам в общем случае выглядит следующим образом:
Коэффициент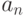 
часто является функцией n. В программе, приведенной выше, рассмотрена аппроксимация симметричной зигзагообразной ломаной линии рядом Фурье. Формула, аппроксимирующая эту линию рядом Фурье, имеет вид
![\limits_{n=1}^{\infty}f(x)=1+\sum(2/\pi n )^2[cos(\pi n) - 1]*cos(\pi n x/2)=](/sites/default/files/tex_cache/83b113a71f40635930cb3b30cc29adc1.png)
Вызов может происходить не только из главной функции, но и из дополнительных функций, однако, в любом случае желательно перед первым вызовом функции поместить ее прототип. В приводимом ниже примере рассчитывается линейная регрессия общего вида.
//==========================================================
// Name : general_linear_regression.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
//Линейная регрессия общего вида
#include<math.h>
#include<stdlib.h>
#define col 20
#define lin 20
#define raw 100
double x[raw];
double y[raw];
double a[col][lin];
double k[col];
double f[col];
int n; //Количество функция
int n1; //Число пар значений
int i,j,i1,i2,t,s2;
double s,s1;
double c;
//Расчетная функция
//Решение системы из N линейных уравнений с N неизвестными методом
//Жордана-Гаусса
void gauss()
{//Прототипы используемых функций
void change();
void devide();
void substraction();
for(s2=1;s2<=n;s2++)
{
for(t=s2;t<=n;t++)
{
if (a[t][s2]==0) {cout<<"\nThere is no single root!"; exit(1);}
else {break;}
}
change();
c=1/a[s2][s2];
devide();
for(t=1;t<=n;t++)
{
if (t==s2) goto alpha;
c=-a[t][s2];
substraction();
alpha: ;
}
}
}
//Функция обмена уравнений
void change()
{double b;
for(j=1;j<=n+1;j++)
{
b=a[s2][j];
a[s2][j]=a[t][j];
a[t][j]=b;
}
}
//Функция деления строки на диагональный элемент
void devide()
{
for(j=1;j<=n+1;j++)
{
a[s2][j]*=c;
}
}
//Функция вычитания умноженной на c s-й строки из t-й строки
void substraction()
{
for(j=1;j<=n+1;j++)
{
a[t][j]+=c*a[s2][j];
}
}
//Функция ввода данных
void input()
{
cout<<"\nInput Functions number, n = "; cin>>n;
cout<<"\nInput value's pairs number, n1 = "; cin>>n1;
for(i=1;i<=n1;i++)
{
cout<<"\nx["<<i<<"] = "; cin>>x[i];
cout<<"\ny["<<i<<"] = "; cin>>y[i];
}
}
//Функция расчета параметров регрессии
void regression()
{ void equations();
void gauss();
for(i=1;i<=n;i++)
{
for(j=1;j<=n+1;j++)
{
a[i][j]=0;
}
}
for(i=1;i<=n1;i++)
{
equations();
for(i1=1;i1<=n;i1++)
{
for(i2=1;i2<=i1;i2++)
{
a[i1][i2]+=f[i1]*f[i2];
a[i2][i1]=a[i1][i2];
}
a[i1][n+1]+=y[i]*f[i1];
}
}
gauss();
}
//Здесь задаются входящие в уравнение функции
void equations()
{
f[1]=pow(x[i],2);
f[2]=exp(x[i]);
f[3]=1/x[i];
}
//Функция вывода
void output()
{void equations();
cout<<"\nRegression's parameters are:";
for(i=1;i<=n;i++)
{
cout<<"\nk["<<i<<"] = "<<a[i][n+1];
}
s=0;
for(i=1;i<=n1;i++)
{
equations();
s1=0;
for(i1=1;i1<=n;i1++)
{
s1+=a[i1][n+1]*f[i1];
}
s+=pow((y[i]-s1),2);
}
cout<<"\nThe sum of square deviations is "<<s<<endl;
}
int main() {
void input();
void regression();
void output();
input();
regression();
output();
return 0;
}
Результат:
Input Functions number, n = 3 Input value's pairs number, n1=5 x[1]=1 y[1]=2 x[2]=2 y[2]=4.5 x[3]=3 y[3]=9.333333 x[4]=4 y[4]=16.25 x[5]=0.5 y[5]=2.25 Regression's parameters are: k[1]=1 k[2]=2.26119e-009 k[3]=1 The sum of square deviations is 2.89343e-016
В приведенном выше примере тела функций были размещены выше главной функции. Вполне допускается размещение тел функций и ниже главной функции, лишь бы их прототипы были своевременно размещены до первого вызова функций. В приводимой ниже программе с помощью кубического сплайна N точками перегиба аппроксимируется функция, заданная таблично.
//==========================================================
// Name : splain_cube_interpolation.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<stdlib.h>
#define array_size 100
double a[array_size][array_size] , h[array_size], d[array_size];
double k[array_size], x[array_size], y[array_size];
int n; //Количество пар значений
int i,j,t,s;
long double c;
long double X; //Неизвестное значение x
long double T,Y;
int main() {
void input();
void sorting();
void calculation();
void function();
void lambda();
input();
sorting();
calculation();
cout<<"\nInput x value, x = ";
cin>>X;
function();
lambda();
cout<<"\nSpline function in "<<X<<" is .. ";
cout<<"\nY("<<X<<") = "<<Y<<endl;
return 0;
}
void calculation()
{
void chainge();
void devision();
void substraction();
for(s=1;s<n;s++)
{
for(t=s;t<=n;t++)
{
if(a[t][s]!=0) goto beta;
}
cout<<"\nThere is no single root!"; exit(1);
beta: chainge();
c=1/a[s][s];
devision();
for(t=1;t<=n;t++)
{
if(t==s) goto gamma;
c=-a[t][s];
substraction();
gamma: ;
}
}
}
void chainge()
{
double b;
for(j=1;j<=n+1;j++)
{
b=a[s][j];
a[s][j]=a[t][j];
a[t][j]=b;
}
}
void devision()
{
for(j=1;j<=n+1;j++)
{
a[s][j]*=c;
}
}
void substraction()
{
for(j=1;j<=n+1;j++)
{
a[t][j]+=c*a[s][j];
}
}
void function()
{
if(X>x[1]) goto teta;
j=1; goto dzeta;
teta: if(X<x[n]) goto psi;
j=n-1; goto dzeta;
psi: for(i=1;i<=n;i++)
{
if(x[i]<X) goto omega;
j=i-1;
i=n;
omega:;
}
dzeta:;
}
void input()
{
cout<<"\nInput number of pairs, n = ";
cin>>n;
for(i=1;i<=n;i++)
{
cout<<"\nx["<<i<<"] = "; cin>>x[i];
cout<<"\ny["<<i<<"] = "; cin>>y[i];
}
}
//Сортировка входных данных по возрастанию X
void sorting()
{
long double H;
long H1;
for(i=1;i<=n-1;i++)
{
H=x[i];
H1=i;
for(j=i+1;j<=n;j++)
{
if (H<x[j]) goto alpha;
H=x[j];
H1=j;
alpha:;
}
x[H1]=x[i];
x[i]=H;
H=y[H1];
y[H1]=y[i];
y[i]=H;
}
for(i=1;i<=n-1;i++)
{
h[i]=x[i+1]-x[i];
d[i]=(y[i+1]-y[i])/h[i];
}
a[1][1]=2;
a[n][n]=2;
a[1][2]=1;
a[n][n-1]=1;
a[1][n+1]=d[1]*3;
a[n][n+1]=d[n-1]*3;
for(i=2;i<=n-1;i++)
{
a[i][n+1]=(d[i]*h[i-1]+d[i-1]*h[i])*3;
a[i][i-1]=h[i];
a[i][i+1]=h[i-1];
a[i][i]=2*(h[i]+h[i-1]);
}
}
void lambda()
{
T=(X-x[j])/h[j];
Y=T*y[j+1]+(1-T)*y[j];
Y+=h[j]*(1-T)*T*((a[j][n+1]-d[j])*(1-T)-(a[j+1][n+1]-d[j])*T);
}
Результат:
Input number of pairs, n = 5 x[1]=0 y[1]=0.1 x[2]=1 y[2]=0.9 x[3]=2 y[3]=3.8 x[4]=3 y[4]=9.2 x[5]=4 y[5]=16 Input x value, x = 4.2 Spline functionin 4.2 is.. Y(4.2)=18.9782
Аналогичным образом размещены прототипы и тела функций в следующей программе, решающей систему нелинейных уравнений методом Ньютона.
//==========================================================
// Name : nonlinear_regression_system.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
#include<stdlib.h>
#define array_size 100 //Размерность массива
long double a[array_size][array_size], b[array_size][array_size];
long double u[array_size][array_size], v[array_size][array_size];
long double w[array_size][array_size];
long double x[array_size], x9[array_size], f[array_size];
long double f9[array_size], f0[array_size], h[array_size];
long n;
long int i,j;
long double of,ff;//Коэффициент оптимизации
int main() {
void input();
void partial_derivative();
void function();
void print();
void inversion_matrix();
void optimization_factor();
n=3;
cout<<"\nApproximated x values input ";
input();
for(int l=0;l<1000;l++)
{
l++;
//Вычисление частных производных
partial_derivative();
for(i=1;i<=n;i++)
{
x[i]=x9[i];
}
//Вызов функций
function();
for(i=1;i<=n;i++)
{
f9[i]=f[i];
}
if(l>997) print();
//Обращение матрицы
inversion_matrix();
//Умножение матриц
for(i=1;i<=n;i++)
{
h[i]=0;
for(j=1;j<=n;j++)
{
h[i]+=w[i][j]*f9[j];
}
}
//Вычисление коэффициента оптимизации
optimization_factor();
for(i=1;i<=n;i++)
{
x9[i]-=of*h[i];
}
}
return 0;
}
void input()
{
for(i=1;i<=n;i++)
{
cout<<"\nx["<<i<<"] = ";
cin>>x[i];
x9[i]=x[i];
}
}
//Вычисление частных производных
void partial_derivative()
{
long double di;
void function();
for(i=1;i<=n;i++)
{
x[i]=x9[i];
}
for(i=1;i<=n;i++)
{
di=fabs(x[i]/1E5)+1E-9;
x[i]+=di;
function();
for(j=1;j<=n;j++)
{
a[j][i]=f[j];
}
x[i]=x9[i];
}
for(i=1;i<=n;i++)
{
di=fabs(x[i]/1E5)+1E-9;
x[i]-=di;
function();
for(j=1;j<=n;j++)
{
a[j][i]=(a[j][i]-f[j])/(2*di);
}
x[i]=x9[i];
}
}
//Здесь описываются функции,
//входящие в уравнения системы
void function()
{
f[1]=pow(x[1],2)-x[2]*x[1]-3;
f[2]=x[3]*x[2]*x[1]-1.5*pow(x[2],2);
f[3]=pow(x[1],3)+pow(x[2],3)+pow(x[3],3)-36;
}
//Вывод результатов на экран
void print()
{
for(i=1;i<=n;i++)
{
cout<<"\nx["<<i<<"] = "<<x9[i];
// <<", f["<<i<<"] = "<<f9[i];
}
cout<<"\n"<<endl;
}
//Обращение матрицы.
//Исходная матрица A,
//Обращенная матрица W
void inversion_matrix()
{
int z,t,k;
double s;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
b[i][j]=0;
v[i][j]=0;
if(i!=j) goto alpha;
b[i][j]=1;
v[i][j]=1;
alpha: ;
}
}
for(z=1;z<=n;z++)
{
s=0;
//Поиск ведущего элемента
for(i=z;i<=n;i++)
{
if(s>fabs(a[i][z])) goto beta;
s=fabs(a[i][z]);
t=i;
beta: ;
}
//Обмен z-й строки с t-й
for(i=1;i<=n;i++)
{
s=a[z][i];
a[z][i]=a[t][i];
a[t][i]=s;
}
if(fabs(a[z][z])>1E-30) goto gamma;
cout<<"\nThe matrix cannot be inversed!"; exit(1);
gamma: v[z][z]=0;
v[t][t]=0;
v[z][t]=1;
v[t][z]=1;
//Исключение недиагональных элементов методом Жордана-Гаусса
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(i==z) goto teta;
if(j==z) goto epsilon;
u[i][j]=a[i][j]-a[z][j]*a[i][z]/a[z][z];
goto psi;
teta: if(i==j) goto omega;
u[i][j]=-a[i][j]/a[z][z];
goto psi;
omega: u[z][z]=1/a[z][z];
goto psi;
epsilon: u[i][z]=a[i][z]/a[z][z];
psi: ;
}
}
//Умножение матриц
//B = V * B
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
w[i][j]=0;
for(k=1;k<=n;k++)
{
w[i][j]+=v[i][k]*b[k][j];
}
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
b[i][j]=w[i][j];
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
a[i][j]=u[i][j];
v[i][j]=0;
if(i==j) v[i][j]=1;
}
}
}
//Результат умножения матрицы A на матрицу B
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
w[i][j]=0;
for(k=1;k<=n;k++)
{
w[i][j]+=a[i][k]*b[k][j];
}
}
}
}
//Вычисление коэффициента оптимизации
void optimization_factor()
{
void function();
double df,s5,s6,s7,ff;
df=0.6;
of=1;
ff=of;
for(i=1;i<=n;i++)
{
x[i]=x9[i]-ff*h[i];
}
s5=0;
function();
for(i=1;i<=n;i++)
{
s5+=pow(f[i],2);
}
for(j=0;j<=3;j++)
{
df*=pow(-0.5,j);
lambda: ff=of+df;
s7=s5;
for(i=1;i<=n;i++)
{
x[i]=x9[i]-ff*h[i];
}
s6=0;
function();
for(i=1;i<=n;i++)
{
s6+=pow(f[i],2);
}
if(s6<s5) s5=s6; of=ff;
if(s6<0.9*s7) goto lambda;
}
}
Результат:
Approximated x values input x[1]=4 x[2]=5 x[3]=6 x[1]=1.73205 x[2]=7.59481e-314 x[3]=3.13474
Можно прототипы функций поместить перед главной функцией, вызовы разместить в главной функции, а описания функций расположить ниже функции main().
В программе zhordan_gauss.cpp производится решение из N линейных уравнений с N неизвестными.
//==========================================================
// Name : zhordan_gauss.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<stdlib.h>
#define col 20 //Количество столбцов
#define lin 20 //Число строк
double a[col][lin]; //Расширенная матрица коэффициентов
int i,j,s,t;
int n; //Количество неизвестных
double c;
//Функция ввода
void input()
{
cout<<"\nInput variables number, n = ";
cin>>n;
cout<<"\nExtended matrix's coefficients input";
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
cout<<"\na["<<i<<"]["<<j<<"] = "; cin>>a[i][j];
}
cout<<"\nb["<<i<<"] = "; cin>>a[i][n+1];
}
}
//Функция обмена уравнений
void change()
{
double b;
for(j=1;j<=n+1;j++)
{
b=a[s][j];
a[s][j]=a[t][j];
a[t][j]=b;
}
}
//Функция деления строки на диагональный элемент
void devide()
{
for(j=1;j<=n+1;j++)
{
a[s][j]*=c;
}
}
//Функция вычитания умноженной на c s-й строки из t-й строки
void substraction()
{
for(j=1;j<=n+1;j++)
{
a[t][j]+=c*a[s][j];
}
}
//Расчетная функция
void gauss()
{
for(s=1;s<=n;s++)
{
for(t=s;t<=n;t++)
{
if (a[t][s]==0) {cout<<"\nThere is no single root!"; exit(1);}
else {break;}
}
change();
c=1/a[s][s];
devide();
for(t=1;t<=n;t++)
{
if (t==s) goto alpha;
c=-a[t][s];
substraction();
alpha: ;
}
}
}
//Функция вывода
void ouput()
{
for(t=1;t<=n;t++)
{
cout<<"\nx["<<t<<"] = "<<a[t][n+1];
}
cout<<"\n"<<endl;
}
int main() {
//Прототипы функций
void input();
void gauss();
void ouput();
input();
gauss();
ouput();
return 0;
}
Результат:
Input variables number, n = 3 Extended matrix's coefficients input a[1][1]=4 a[1][2]=7 a[1][3]=2 b[1]=38 a[2][1]=6 a[2][2]=3 a[2][3]=2 b[2]=26 a[3][1]5= a[3][2]=-2 a[3][3]=-3 b[3]=-1 x[1]=2 x[2]=4 x[3]=1
Передача массивов в качестве параметров
Массивы могут быть параметрами функций, и функции могут возвращать указатель на массив в качестве результата.
Меньше всего возникает проблем при работе с массивами символов (со стоками). В программе array_func приводится пример использования массива указателей на строки в качестве параметра функции.
//==========================================================
// Name : array_func.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<string.h>
void print(int n, char *Name[])
{
for(int i=0;i<n;i++)
{
cout<<"\nMy ["<<i+1<<"] friend name is "<<Name[i];
}
cout<<"\n"<<endl;
}
int main() {
//Прототип функции печати
void print(int n, char *Name[]);
//Массив указателей на строки
char *Name[]={"Airat", "Nail", "Rustem","Almaz"};
//Определим размер массива *Name[]
int n=strlen(*Name)-1;
print(n, Name);
return 0;
}
Результат:
My [1] friend name is Airat My [2] friend name is Nail My [3] friend name is Rustem My [4] friend name is Almaz
Если массив-параметр не является символьной строкой, то необходимо передавать в функцию либо массив фиксированного заранее определенного размера, либо передавать размер массива с помощью дополнительного параметра. В следующем примере рассматривается проверка достоверности различий между двумя выборками по критерию Стьюдента. В функцию передаются два вещественных массива, а из функции возвращаются пять вещественных чисел (допускается использование нескольких операторов return).
//==========================================================
// Name : student.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>//Стандартная математическая библиотека
//В качестве параметров функции могут выступать массивы,
//например, a[], b[].
//Функция расчета величины критерия Стьюдента
//Глобальные переменные
double av_a, av_b, sigma_a, sigma_b;
double student(int n, double a[], double b[])
{
double sum_a=0;//Сумма массива a[]
double sum_b=0;//Сумма массива b[]
for(int i=0;i<n;i++)
{
sum_a=sum_a+a[i];
sum_b=sum_b+b[i];
}
av_a=sum_a/n;//Среднее арифметическое массива a[]
av_b=sum_b/n;//Среднее арифметическое массива b[]
double d_a=0;//Сумма квадратов отклонений массива a[]
double d_b=0;//Сумма квадратов отклонений массива b[]
for(int i=0;i<n;i++)
{
d_a=d_a+pow((a[i]-av_a), 2);
d_b=d_b+pow((b[i]-av_b), 2);
}
sigma_a=sqrt(d_a/(n-1)); //Среднее квадратическое отклонение
sigma_b=sqrt(d_b/(n-1));
double m_d=sqrt(pow((sigma_a),2)+pow((sigma_b),2));
double d=av_a-av_b; //Разность выборочных средних
double t_imperical=d/m_d;//Имперический коэффициент Стьюдента
return fabs(t_imperical);
return av_a;
return av_b;
return sigma_a;
return sigma_b;
}
int main() {
double a[]={1.2, 1.3, 1.25, 1.28, 1.13};
double b[]={3.8, 3.64, 3.15, 3.863, 3.13};
//Определим размер массивов
int n=sizeof(a)/sizeof(a[0]);
double t=student(n, a, b);
double z;
int st=2*(n-1);//Число степеней свободы
//Введем таблицу Стьюдента для 95% вероятности
if (st>120) z=1.96;
else if (st==120) z=1.98;
else if (st>=100) z=1.982;
else if (st>=90) z=1.986;
else if (st>=80) z=1.989;
else if (st>=70) z=1.994;
else if (st>=60) z=2;
else if (st>=55) z=2.004;
else if (st>=50) z=2.008;
else if (st>=45) z=2.014;
else if (st>=40) z=2.021;
else if (st>=35) z=2.030;
else if (st>=30) z=2.042;
else if (st==29) z=2.045;
else if (st==28) z=2.048;
else if (st==27) z=2.052;
else if (st==26) z=2.056;
else if (st==25) z=2.060;
else if (st==24) z=2.064;
else if (st==23) z=2.069;
else if (st==22) z=2.074;
else if (st==21) z=2.080;
else if (st==20) z=2.086;
else if (st==19) z=2.093;
else if (st==18) z=2.101;
else if (st==17) z=2.110;
else if (st==16) z=2.120;
else if (st==15) z=2.131;
else if (st==14) z=2.145;
else if (st==13) z=2.160;
else if (st==12) z=2.179;
else if (st==11) z=2.201;
else if (st==10) z=2.228;
else if (st==9) z=2.262;
else if (st==8) z=2.306;
else if (st==7) z=2.365;
else if (st==6) z=2.447;
else if (st==5) z=2.571;
else if (st==4) z=2.776;
else if (st==3) z=3.182;
else if (st==2) z=4.303;
else if (st==1) z=12.706;
else cout<<"\nThats all right!"<<endl;
cout<<"\nFirst sample: "<<av_a<<" +/- "<<3*sigma_a;
cout<<"\nSecond sample: "<<av_b<<" +/- "<<3*sigma_b;
cout<<"\nImperical t-test value = "<<t;
cout<<"\nStandard t-test value = "<<z;
if (t>z) cout<<"\nDifferences are valid because "<<t<<" > "<<z<<""<<endl;
else cout<<"\nDifferences are invalid because "<<t<<" < "<<z<<""<<endl;
return 0;
}
Результат:
First sample : 1.232 +/- 0.205012 Second sample: 3.5166 +/- 1.06001 Imperical t-test value = 6.34812 Standard t-test value = 2.306 Differences are valid because 6.34812 > 2.306
Правила области видимости
Область видимости (действия) переменной, если она используется в функции относится к диапазону, где эта функция доступна. Переменные могут иметь локальную и глобальную области видимости, а также область видимости классов.
Локальную переменную можно использовать в описании функции. Тогда область ее видимости ограничена только этой функцией. Эта переменная считается доступной только внутри данной функции (например, переменные a и b действуют только в пределах главной функции программы function_1).
Переменные с глобальной областью видимости объявляются вне каких-либо функций или классов. Эти переменные доступны во всем файле и имеют глобальную область видимости (например, переменные x и y в программе function_1).
С вопросом об области видимости переменных тесно связана проблема задания типа функций. Если определить переменные, используемые в некоторой функции и в главной функции в области глобальных переменных, то функции незачем возвращать значения (она может иметь тип void), однако, если все переменные задаются в главной функции, то функции уже должны возвращать значения. Сказанное проиллюстрировано двумя программами, рассчитывающими величину критерия Фишера. Программы дают одинаковый результат, однако, их функции имеют разную область видимости переменных.
//==========================================================
// Name : function_vision_1.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
//Область глобальных переменных
////////////////////////////////
int i;
double sum_a, sum_b;
double sum_sqr_a, sum_sqr_b;
double av_a, av_b;
double S_a, S_b;
double F;
///////////////////////////////
double a[]={3, 4, 5, 8, 9, 1, 2, 4, 5};
double b[]={6, 19, 3, 2, 14, 4, 5, 17, 1};
int n=sizeof(a)/sizeof(a[0]);
////////////////////////////////
void sum()
{
sum_a=0;
sum_b=0;
for(i=0;i<n;i++)
{
sum_a+=a[i];
sum_b+=b[i];
}
}
void sum_sqr()
{
av_a=sum_a/n;//Среднее арифметическое первого массива
av_b=sum_b/n;//Среднее арифметическое второго массива
sum_sqr_a=0;
sum_sqr_b=0;
for(i=0;i<n;i++)
{
sum_sqr_a+=pow((av_a-a[i]),2);
sum_sqr_b+=pow((av_b-b[i]),2);
}
}
void variance()
{
S_a=sum_sqr_a/(n-1);
S_b=sum_sqr_b/(n-1);
}
void Fisher()
{
if (S_a>S_b) {F=S_a/S_b;}
else F=S_b/S_a;
}
int main() {
void sum();
sum();
void sum_sqr();
sum_sqr();
void variance();
variance();
void Fisher();
Fisher();
cout<<"\nF = "<<F<<endl;
return 0;
}
Результат:
F criteria is 6.95082
Рассмотрим аналогичный пример.
//==========================================================
// Name : function_vision_2.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
double sum(int n, double a[])
{
double sum=0;
for(int i=0;i<n;i++)
{
sum+=a[i];
}
return sum;
}
double sum_sqr(int n, double a[], double sum)
{
double av=sum/n;//Среднее арифметическое массива
double sum_sqr=0;
for(int i=0;i<n;i++)
{
sum_sqr+=pow((av-a[i]),2);
}
return sum_sqr;
}
double variance(int n, double sum_sqr)
{
double S=sum_sqr/(n-1);
return S;
}
double Fisher(double S_a, double S_b)
{
double F;
if (S_a>S_b) {F=S_a/S_b;}
else {F=S_b/S_a;};
return F;
}
int main() {
double sum_a, sum_b; //Суммы массивов
double sum_sqr_a, sum_sqr_b; //Суммы квадратов отклонений
double S_a, S_b; //Дисперсии
double F; //Величина F-критерия
double a[]={3, 4, 5, 8, 9, 1, 2, 4, 5};
double b[]={6, 19, 3, 2, 14, 4, 5, 17, 1};
int n=sizeof(a)/sizeof(a[0]);
//Прототип функции
double sum(int n, double a[]);
sum_a=sum(n,a);
sum_b=sum(n,b);
double sum_sqr(int n, double a[], double sum);
sum_sqr_a=sum_sqr(n,a,sum_a);
sum_sqr_b=sum_sqr(n,b,sum_b);
double variance(int n, double sum_sqr);
S_a=variance(n,sum_sqr_a);
S_b=variance(n,sum_sqr_b);
double Fisher(double S_a, double S_b);
F=Fisher(S_a,S_b);
cout<<"\nF criteria is "<<F<<endl;
return 0;
}
Результат:
F criteria is 6.95082
Передача в функцию указателей на массивы
В качестве аргументов функций могут выступать указатели на массивы. При этом в ходе выполнения тела цикла массивы могут быть изменены. В следующем примере определяются коэффициенты линейной регрессии с учетом весовых коэффициентов.
//==========================================================
// Name : lin_regression.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
//Вспомогательные функции
double s_2(int n, double *x, double *w)
{
double s2=0;
for(int i=0;i<n;i++)
{
s2+=x[i]*w[i];
}
return s2;
}
double s_3(int n, double *y, double *w)
{
double s3=0;
for(int i=0;i<n;i++)
{
s3+=y[i]*w[i];
}
return s3;
}
double s_4(int n, double *x, double *w)
{
double s4=0;
for(int i=0;i<n;i++)
{
s4+=w[i]*pow(x[i],2);
}
return s4;
}
double s_5(int n, double *x, double *y, double *w)
{
double s5=0;
for(int i=0;i<n;i++)
{
s5+=x[i]*y[i]*w[i];
}
return s5;
}
//Функция расчета стандартного отклонения
double sigma(int n, double *y, double *x, double a, double b, double *w)
{
double sigma=0;
for(int i=0;i<n;i++)
{
sigma+=w[i]*pow((y[i]-(a+b*x[i])),2);
}
return sigma;
}
//Функция печати
void print(double *x, double *y, double a, double b, int n)
{
for(int i=0;i<n;i++)
{
cout<<"\nx ["<<i+1<<"] = "<<x[i]<<", y ["<<i+1<<"] = "<<y[i]<<", y(calc) ["<<i+1<<"] = "<<a+b*x[i];
}
}
//Функция расчета коэффициентов регрессии
void regression(double a, double b, double f)
{
cout<<"\ny("<<f<<") = "<<a<<" + "<<b<<"*"<<f<<" = "<<a+b*f<<endl;
}
int main() {
//Прототипы функций:
double s_2(int n, double *x, double *w);
double s_3(int n, double *y, double *w);
double s_4(int n, double *x, double *w);
double s_5(int n, double *x, double *y, double *w);
double sigma(int n, double *y, double *x, double a, double b, double *w);
double x[]={2.1, 3.9, 5.1, 5.8};//Первый массив
double y[]={4.1, 8.1, 9.9, 12.1};//Второй массив
double w[]={0.5, 3, 10, 1};//Весовые коэффициенты
int n=sizeof(x)/sizeof(x[0]);
int s1=n;
double s2=s_2(n,x,w);
double s3=s_3(n,y,w);
double s4=s_4(n,x,w);
double s5=s_5(n,x,y,w);
double d1=s1*s4-s2*s2;
double a=(s3*s4-s5*s2)/d1;
double b=(s1*s5-s2*s3)/d1;
double sig=sigma(n,y,x,a,b,w);
//Стандартное отклонение
double D=sqrt(sig/(n-2));
cout<<"\ny = "<<b<<" * x + ("<<a<<") ";
cout<<"\nThe sum of square deviations is "<<sig;
cout<<"\nStandard deviation = "<<D;
cout<<"\nThe number of pairs = "<<s1<<endl;
cout<<"\nLets compare initial values with calculated ones";
void print(double *x, double *y, double a, double b, int n);
print(x,y,a,b,n);
double f;
cout<<"\nEnter some x value ";
cin>>f;
void regression(double a, double b, double f);
regression(a,b,f);
return 0;
}
Результат:
y=1.9773*x+(-0.0178638) The sum of square deviations is 1.19472 Standard deviation = 0.772891 The number of pairs = 4 Lets compare initial values with calculated ones x[1] = 2.1, y[1] = 4.1, y(calc)[1] = 4.13447 x[2] = 3.9, y[2] = 8.1, y(calc)[2] = 7.69362 x[3] = 5.1, y[3] = 9.9, y(calc)[3] = 10.0664 x[4] = 5.8, y[4] = 12.1, y(calc)[4] = 11.4505 Enter some x value 5 y(5)=-0.0178638+1.9773*5=9.86865
Вызов функции по указателю
При вызове функции через указатель нужно помнить, что функции характеризуются возвращаемым значением, именем и сигнатурой (количеством, порядком следования и типом параметров). Указатель на функцию определяется следующим образом.
тип функции (*имя указателя) (спецификация параметров);
В определении указателя на функцию тип возвращаемого значения и сигнатуры должны совпадать с соответствующими типами и сигнатурами тех функций, адреса которых предполагается присваивать вводимому указателю при инициализации или с помощью оператора присваивания.
Например, int(*alpha)(double) – определение указателя alpha на функцию с параметром типа double, возвращающую значение типа int.
Для функций с большим количеством параметров и сложным описанием возвращаемых значений описание указателя на функцию может оказаться слишком громоздким. Для удобства последующих применений и сокращения производных описаний рекомендуется вводить имя типа указателя на функции с помощью оператора typedef. Например:
typedef double(*Beta)(char);
Здесь Inter – имя типа "указатель на функцию с параметром типа char, возвращающую значение типа double". Вводя имена указателей на функции проще описать соответствующие указатели, массивы и другие производные типы.
Указатели на функции очень удобны в тех случаях, когда объектами обработки служат функции, например, при построении таблицы значений заданной функции. Удобнее всего организовать связь между функцией, реализующей метод обработки (например, численное интегрирование), и той функцией, для которой этот метод нужно применить через аппарат параметров, в число которых входят указатели на функции.
Рассмотрим следующую задачу. Требуется сравнить эффективность трех методов численного интегрирования (метод прямоугольников, метод Симпсона и метод Эйлера) при различном количестве итераций с аналитическим решением уравнения на отрезке [A,B]. Численное интегрирование методом прямоугольников (интегрирование методом Симпсона и Эйлера производится аналогично) оформляется в виде функции со следующим заголовком:
double root(Указатель_на_функцию, double A, double B, int n)
Где А – нижний предел интегрирования, В – верхний предел, n – количество итераций. Введем тип "указатель на функцию", для которой нужно найти корень:
typedef double(*Inter)(double);
Теперь можно определить функцию для вычисления корня заданной функции с указателем Inter. Ее прототип будет таким:
double root(Inter F, double A, double B, int n)
Подынтегральная функция (y=x2) задается в функции double Integral(double x). Ниже приводится листинг программы, сравнивающей три метода численного интегрирования на отрезке [1,3] при разном количестве итераций.
//==========================================================
// Name : integral_point_call.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
#define l 1 //Нижний предел интегрирования
#define u 3 //Верхний предел интегрирования
//Подынтегральная функция задается здесь
double Integral(double x)
{
return pow(x,2);
}
//Первообразная (для сравнения результатов)
double standard()
{
return (pow(u,3)-pow(l,3))/3;
}
//Интегрирование произвольной функции методом прямоугольников
//Определим тип указателя на функцию
typedef double(*Inter)(double);
double root(Inter F, double A, double B, int n)
{
double delta=(B-A)/n;//Приращение (шаг итерации)
double S=0;//Интеграл
double d; //xi
double g; //f(xi) - значение функции в точке xi
for(int i=0;i<n;i++)
{
d=A+i*delta;//xi
g=(*F)(d); //f(xi) - значение функции в точке xi
{if (g<=0) continue;}//Отбрасываем отрицательные значения
S+=g;
}
S=S*delta;//Интеграл
return S;
}
//Интегрирование произвольной функции методом Симпсона
typedef double(*Inter_simpson)(double);
double root_simpson(Inter_simpson G,double A,double B, int n)
{
int n1=4;
double S=0;//Интеграл
double delta;//Шаг
double x;
for(int i=0;i<n;i++)
{
delta=(B-A)/n1;
S=(*G)(A);
for(i=1;i<n1-1;i+=2)
{
x=A+i*delta;
S+=4*(*G)(x);
}
for(i=2;i<n1-2;i+=2)
{
x=A+i*delta;
S+=2*(*G)(x);
}
S+=(*G)(B);
S=(S*delta)/3;
n1=n1*2;
}
return S;
}
//Интегрирование произвольной функции методом Эйлера
typedef double(*Inter_euler)(double);
double root_euler(Inter_euler K, double A, double B, int n)
{
double S=0; //Интеграл
double delta=(B-A)/n;//Шаг интегрирования
double x=A;
double y=(*K)(x);
S+=y/2;
for(x=A+delta;x<B-delta;x+=delta)
{
y=(*K)(x);
S+=y;
}
x=B;
y=(*K)(x);
S+=y/2;
S*=delta;
return S;
}
int main() {
double root (Inter, double, double, int);
double result;
double root_simpson (Inter_simpson, double, double, int);
double result_simpson;
double root_euler (Inter_euler, double, double, int);
double result_euler;
cout<<"\nIntegration of y=x^2,";
cout<<"\nlower level is "<<l<<", upper level is "<<u<<" ";
double standard();
double st=standard();
cout<<"\nStandard root of equation is "<<st<<endl;
for(int i=100;i<=1000;i+=100)
{
result =root (Integral, l, u, i);
result_simpson =root_simpson (Integral, l, u, i);
result_euler =root_euler (Integral, l, u, i);
cout<<"\nrctg["<<i<<"]="<<result<<", simpson["<<i<<"]="<<result_simpson<<", euler["<<i<<"]="<<result_euler;
}
cout<<"\n"<<endl;
return 0;
}
Результат:
Integration of y=x^2, lower level is 1, upper level is 3 Standard root of equation is 8.66667 rctg[100]=8.5868, simpson[100]=8.38931, euler[100]=8.48919 rctg[200]=8.6267, simpson[200]=8.52702, euler[100]=8.6667 rctg[300]=8.64001, simpson[300]=8.5966, euler[100]=8.60695 rctg[400]=8.64668, simpson[400]=8.5966, euler[100]=8.66667 rctg[500]=8.65067, simpson[500]=8.63157, euler[100]=8.63077 rctg[600]=8.65334, simpson[600]=8.63157, euler[100]=8.63674 rctg[700]=8.65524, simpson[700]=8.63157, euler[100]=8.66667 rctg[800]=8.65667, simpson[800]=8.63157, euler[100]=8.66667 rctg[900]=8.65778, simpson[900]=8.63157, euler[100]=8.66667 rctg[1000]=8.65867, simpson[1000]=8.63157, euler[1000]=8.66667
В следующей программе сравниваются три метода решения дифференциальных уравнений: метод Эйлера, метод прогноза и коррекции, метод Рунге-Кутты-Нистрема:
//==========================================================
// Name : root.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
double y;
double x9,y9,d;
//Аналитическое решение дифференциального уравнения
double standard(double e)
{
return exp(pow(e,2)/2);
}
//Здесь задается правая часть дифференциального уравнения
double Equation(double x9, double y9)
{
d=x9*y9;
return d;
}
//Определим тип указателя на функцию
typedef double(*Eul)(double,double);
//Решение дифференциального уравнения методом Эйлера
double Euler(Eul G, double a,double e,double h, double y1)
{
y9=y1;
for(x9=a;x9<e-h;x9+=h)
{
(*G)(x9,y9);
y9+=d*h;
}
return y;
}
//Определим тип указателя на функцию
typedef double(*Imp_Euler)(double,double);
//Решение дифференциальных уравнений улучшенным методом Эйле-ра,
//Метод прогноза и коррекции
double Improoved_Euler(Imp_Euler F, double a,double e,double h, double y1)
{
y=y1;
double x;
double y2,y3;
for(x=a;x<e-h;x+=h)
{
x9=x;
y9=y;
(*F)(x9,y9);
y2=y+d*h;
x9=x+h;
y9=y2;
(*F)(x9,y9);
y3=y+d*h;
y=(y2+y3)/2;
}
return y;
}
//Определим тип указателя на функцию
typedef double(*Runge)(double,double);
//Решение дифференциального уравнения методом Рунге-Кутта-Нистрема
double Runge_Kutta_Nistrem(Runge R,double a,double e,double h, double y1)
{
y=y1;
double x;
double k1,k2,k3,k4;
for(x=a;x<e-h;x+=h)
{
x9=x;
y9=y;
(*R)(x9,y9);
k1=h*d;
x9=x+h/2;
y9=y+k1/2;
(*R)(x9,y9);
k2=h*d;
x9=x+h/2;
y9=y+k2/2;
(*R)(x9,y9);
k3=h*d;
x9=x+h;
y9=y+k3;
(*R)(x9,y9);
k4=h*d;
y+=(k1+2*k2+2*k3+k4)/6;
}
return y;
}
int main() {
double standard(double e);
double Euler(Eul G, double a,double e,double h, double y1);
double rEul;
double Improoved_Euler(Imp_Euler F, double a,double e,double h, double y1);
double rImpEul;
double Runge_Kutta_Nistrem(Runge R,double a,double e,double h, double y1);
double rRunge;
double y1;//Начальное значение Y
double a; //Начальное значение X
double e; //Конечное значение X
double h; //Шаг
cout<<"\nInput initial y value, = ";
cin>>y1;
cout<<"\nInput initial x value, = ";
cin>>a;
cout<<"\nInput final x value, = ";
cin>>e;
int n1=2;
cout<<"\nDifferential equation: dy/dx=x*y";
cout<<"\nStandard root of equation is "<<standard(e);
for (n1=100;n1<150000;n1+=15000)
{
h=(e-a)/n1;
rEul=Euler(Equation,a,e,h,y1);
rImpEul=Improoved_Euler(Equation,a,e,h,y1);
rRunge=Runge_Kutta_Nistrem(Equation,a,e,h,y1);
cout<<"\nEuler["<<n1<<"]="<<rEul<<", Improoved Euler["<<n1<<"]="<<rImpEul<<", Runge["<<n1<<"]="<<rRunge;
n1=n1*2;
}
cout<<"\n"<<endl;
return 0;
}
Результат:
Input initial y value, = 1 Input initial x value, = 0 Input final x value, = 1 Differential equation: dy/dx=x*y Standard root of equation is 1.64872 Euler[100]=0, Improoved Euler[100]=1.63239, Runge[100]=1.6324 Euler[15200]=1.6324, Improoved Euler[15200]=1.64872, Runge[15200]=1.64872 Euler[45400]=1.64872, Improoved Euler[45400]=1.64868, Runge[45400]=1.64868 Euler[105800]=1.64868, Improoved Euler[105800]=1.64871, Runge[105800]=1.64871
В следующей программе сравниваются два метода решения систем дифференциальных уравнений: метод Эйлера и метод Рунге-Кутты-Нистрема.
//==========================================================
// Name : Euler_Runge_Kutta.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
#define array_size 20
#define n 2
double alpha[array_size];
double y[array_size];
int i,n1;
double d[array_size];
double dzeta;
//Здесь задаются правые части дифференциальных уравнений
double Equation(double alpha[array_size], double dzeta)
{
d[1]=-3*pow(alpha[1],2)+ 2*alpha[2]+exp(-dzeta);
d[2]= 3*pow(alpha[1],2)-12*alpha[2]+exp(-dzeta);
return d[1];
return d[2];
}
//Определим тип указателя на функцию
typedef double(*Eul)(double[array_size],double);
//Решение правой части дифференциальных уравнений
//Решение методом Эйлера
double Euler(Eul G, double h,double a,double e,double beta[array_size])
{
double Equation(double alpha[array_size], double dzeta);
for(i=1;i<=n;i++)
{
alpha[i]=beta[i];
}
for(dzeta=a;dzeta<e-h;dzeta+=h)
{
(*G)(alpha,dzeta);
for(i=1;i<=n;i++)
{
alpha[i]+=d[i]*h;
}
}
return alpha[i];
}
//Определим тип указателя на функцию
typedef double(*Runge_Kutta)(double[array_size],double);
//Вычисление правой части дифференциального уравнения
//Решение методом Рунге-Кутты-Нистрема
double Runge(Runge_Kutta R,double h,double a,double e,double beta[array_size])
{
double Equation(double alpha[array_size],double dzeta);
double x;
double k1 [array_size];
double k2 [array_size];
double k3 [array_size];
double k4 [array_size];
int i9;
for(i=1;i<=n;i++)
{
y[i]=beta[i];
}
for(i9=0;i9<=(n1-1);i9++)
{
x=a+i9*h;
dzeta=x;
for(i=1;i<=n;i++)
{
alpha[i]=y[i];
}
(*R)(alpha,dzeta);
for(i=1;i<=n;i++)
{
k1[i]=h*d[i];
}
dzeta=x+h/2;
for(i=1;i<=n;i++)
{
alpha[i]=y[i]+k1[i]/2;
}
(*R)(alpha,dzeta);
for(i=1;i<=n;i++)
{
k2[i]=h*d[i];
}
dzeta=x+h/2;
for(i=1;i<=n;i++)
{
alpha[i]=y[i]+k2[i]/2;
}
(*R)(alpha,dzeta);
for(i=1;i<=n;i++)
{
k3[i]=h*d[i];
}
dzeta=x+h;
for(i=1;i<=n;i++)
{
alpha[i]=y[i]+k3[i];
}
(*R)(alpha,dzeta);
for(i=1;i<=n;i++)
{
k4[i]=h*d[i];
}
for(i=1;i<=n;i++)
{
y[i]+=(k1[i]+2*k2[i]+2*k3[i]+k4[i])/6;
}
}
return y[i];
}
int main() {
double Euler(Eul G,double h,double a,double e,double beta[array_size]);
double Runge(Runge_Kutta R,double h,double a,double e,double beta[array_size]);
double a;//initial x value
double e;//final x value
double h;//The step
double beta[array_size];
for(int i=1;i<=n;i++)
{
cout<<"\nInput y["<<i<<"] = "; cin>>beta[i];
}
cout<<"\nInput initial x value = ";cin>>a;
cout<<"\nInput final x value = ";cin>>e;
n1=4;
cout<<"\nThe first equation is dy/dx=-3*y[1]*y[1]+2*y[2]+exp(-x)";
cout<<"\nThe second equation is dy/dx=3*y[1]*y[1]-12*y[2]+exp(-x)";
for (n1=10;n1<50;n1+=10)
{
h=(e-a)/n1;
Euler(Equation,h,a,e,beta);
Runge(Equation,h,a,e,beta);
cout<<"\n"<<n1<<" partitional intervals";
for(i=1;i<=n;i++)
{
cout<<"\nEuler["<<i<<"] = "<<alpha[i]<<", Runge["<<i<<"] = "<<y[i];
}
n1=n1*2;
}
cout<<"\n";
return 0;
}
Результат:
Input y[1]=1 Input y[2]=1 Input initial x value =0 Input final x value =1 The first equation is dy/dx=-3*y[1]*y[1]+2*y[2]+exp(-x) The second equation is dy/dx=3*y[1]*y[1]-12*y[2]+exp(-x) 10 partitional intervals Euler[1]=0.528479, Runge[1]=0.528505 Euler[2]=0.109339, Runge[2]=0.109586 30 partitional intervals Euler[1]=0.528515, Runge[1]=0.528516 Euler[2]=0.109555, Runge[2]=0.109561
В данном примере приводится алгоритм нахождения производных двух функций, вызываемых через указатель.
//==========================================================
// Name : p_function.cpp
// Author : Marat
// Version :
// Copyright : Your copyright notice
// Description : Hello World in C++, Ansi-style
//==========================================================
#include <iostream>
using namespace std;
#include<math.h>
//Определим тип указателя на функцию
//dif - функция дифференцирования
typedef double(*dif)(double);
//Зададим I функцию
double difer(double x)
{
return pow(x,2);
}
//Зададим II функцию
double difer_1(double x)
{
double gamma = pow(x,3)+5;
return gamma;
}
//Функция расчета производной в середине интервала между В и А
double root(dif F, double c, int n)
{
double delta=2*c/n;
double g=((*F)(c+delta)-(*F)(c))/delta; //производная в точке, лежащей на середине отрезка
return g;
}
int main() {
int n=1000000;
double c;
cout<<"\nInput quantity, please, x = ";
cin>>c;
double root(dif, double, int);//Прототип функции
double result;//I Результат
result=root(difer, c, n);
cout<<"\ny = x^2, y'("<<c<<") = "<<result<<endl;
double result_1;//II Результат
result_1=root(difer_1, c, n);
cout<<"\ny = x^3+5, y'("<<c<<") = "<<result_1<<endl;
return 0;
}
Результат:
Input quantity please, x = 6 y = x^2, y'(6) = 12 y = x^3+5, y'(6) =108
< Лекция 10 || Лекция 11 || Лекция 12 >
