Разработка полноценных Windows-приложений
Приложение "Интерполяционный полином"
В данном параграфе на примере написания приложения "Интерполяционный полином" рассматриваются следующие вопросы: графический вывод, работа с курсором и мышью, работа с модальными диалоговыми окнами, работа с растровыми изображениями, работа с панелями управления и строками состояния, работа с полиномами.
Постановка задачи. Теоретический материал
Пусть у нас есть следующая таблица:
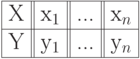
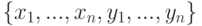
Требуется построить полином y=f(x), принимающий значения согласно таблице. Интерполяционный полином - полином, принимающий значения y в точках x согласно указанной таблице. Значения x называются узлами интерполяции.
Существуют разные алгоритмы построения интерполяционного полинома, мы воспользуемся методом Лагранжа. Данный метод дает аналитическое представление интерполяционного полинома в следующем виде:
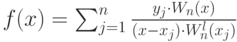
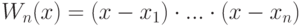
Для построения интерполяционного полинома напишем Windows приложение с графическим интерфейсом, удовлетворяющим следующим требованиям:
- должна быть реализована возможность ввода узлов интерполирования двумя способами: с клавиатуры, посредством мыши;
- должен быть реализован вывод аналитической формулы и графика полинома на экран, сохранение изображения графика в файл;
- должна быть реализована возможность параллельного переноса центра системы координат и ее масштабирование.
Согласно требованиям, наша программа должна осуществлять полноценный графический вывод информации на экран. При этом возникает проблема аппаратно-независимого вывода изображения. Каждое Windows окно имеет собственную стандартную (аппаратную) систему координат.
Стандартная (аппаратная) система координат - левая система координат с центром в левом верхнем углу окна. Ось X направлена вправо, а ось Y вниз. Единица измерения - 1 пиксель.
Стандартные координаты аппаратно зависимы. А это значит, что на разных мониторах и принтерах изображения размером n?n пикселей будут иметь различные размеры, в зависимости от размеров пикселей поддерживаемых устройством вывода. Аппаратная зависимость координат также не позволяет выводить на экран изображения, размеры которых превосходят размеры клиентской области окна. Для преодоления аппаратной зависимости необходимо выполнить преобразование координат.
Принципы построения собственных функций преобразования координат
Чтобы реализовать аппаратно независимый вывод графики, можно ввести 2 логические системы координат: видимую и невидимую и организовать переход от одной к другой. Видимая система координат - основная, она и определяет логические координаты точек. Невидимая система координат - вводится для реализации точки наблюдения. рис. 5.1
Геометрический смысл преобразования. Переход от стандартной системы координат к видимой логической выполняется для преодоления проблемы несоответствия размеров пикселей на разных устройствах. А переход от видимой логической системы координат к невидимой системе координат необходим, если требуется отобразить ту часть изображения, которая не помещается в окне.
Математическая реализация. Пусть (a,b) - координаты центра видимой логической системы координат в стандартной системе координат, а (c,d) - координаты точки наблюдения в видимой логической системе координат. Тогда формула для выполнения нужного перехода:
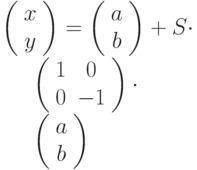
S - коэффициент масштабирования (он выбирается в зависимости от характеристик монитора). Теперь, пользуясь этой формулой, можно, зная логические координаты, переходить к системным координатам, что необходимо для рисования. А так же, изменяя координаты точки наблюдения, отображать невидимые ранее части образа. Нетрудно получить и обратное выражение логических координат через системные координаты. Это нужно, чтобы выводить информацию о положении на плоскости.
Проектирование и разработка приложения
Этапы разработки
- Написать функции перехода от логических координат к системным координатам и наоборот.
- Реализовать операции параллельного переноса центра логической системы координат и масштабирования.
- Организовать ввод начальных данных.
- Построить интерполяционный полином по введенным данным.
- Организовать вывод результатов.
Создадим с помощью мастера MFC стандартное SDI приложение "Gp", с поддержкой архитектуры "документ-вид". Отключим поддержку символов Unicode.
1. Функции перехода от логических координат к системным координатам и наоборот
Логические координаты на плоскости представляют собой упорядоченную пару вещественных чисел. Для их программной реализации следует ввести структуру SDPoint. Вынесем ее в новый заголовочный файл (например, DoublePoint.h )
struct SDPoint
{
double x;
double y;
};Далее приведен полный исходный код класса вида CGpView программы. Пояснения ко всем введенным переменным, функциям и обработчикам приведены в пунктах, при реализации которых использовались эти элементы. В рамках данного пункта рассмотрим функции перехода от системных координат к логическим координатам, выделенные жирным шрифтом.
// GpView.h : interface of the CGpView class
#pragma once
class CGpView : public CView
{
protected: // create from serialization only
CGpView();
DECLARE_DYNCREATE(CGpView)
// Attributes
public:
CGpDoc* GetDocument() const;
// Operations
public:
// Overrides
public:
virtual void OnDraw(CDC* pDC); // overridden to draw this view
virtual BOOL PreCreateWindow(CREATESTRUCT& cs);
protected:
// Implementation
public:
virtual ~CGpView();
#ifdef _DEBUG
virtual void AssertValid() const;
virtual void Dump(CDumpContext& dc) const;
#endif
protected:
// Generated message map functions
protected:
DECLARE_MESSAGE_MAP()
private: //Добавляем необходимые переменные
int ScaleXY; //Масштабный коэффициент (сколько пикселей в логической единице)
SDPoint CameraPoint; //Логические координаты точки наблюдения
bool parallel_shift; //флаг для входа(выхода) в(из) режим(а) параллельного переноса
bool move_camera; //флаг для активации параллельного переноса
CPoint MousePosPoint; //Системные координаты курсора мыши
CFont axisFont; //Шрифт для подписи осей
CPen polPen; //Перо для рисования графика полинома
bool mark_points; //Флаг для входа(выхода) в(из) режим(а) визуального
редактирования узлов интерполирования
CImage imgOriginal; //Переменная для сохранения изображения клиентской области окна (графика)
public: //Необходимые функции
SDPoint SysToLog(CPoint SysPoint); //Функция перехода от системных к логическим координатам
CPoint LogToSys(double xl, double yl); //Функция перехода от логических коодинат к системным
void DrawAxis(CDC* pDC); //Функция для прорисовки осей
void DrawPolinom(CDC* pDC); //Функция для прорисовки полинома
void DrawInitPoints(CDC* pDC); //Функция для прорисовки узлов интерполяции
public: //Обработчики (добавлены с помощью мастера)
afx_msg void OnMouseMove(UINT nFlags, CPoint point);
afx_msg void OnLButtonDown(UINT nFlags, CPoint point);
afx_msg void OnToolsParallelshift();
afx_msg void OnUpdateToolsParallelshift(CCmdUI *pCmdUI);
afx_msg void OnLButtonUp(UINT nFlags, CPoint point);
afx_msg BOOL OnMouseWheel(UINT nFlags, short zDelta, CPoint pt);
afx_msg void OnToolsAddpoint();
afx_msg void OnToolsMarkinitialpoints();
afx_msg void OnUpdateToolsMarkinitialpoints(CCmdUI *pCmdUI);
afx_msg void OnLButtonDblClk(UINT nFlags, CPoint point);
afx_msg void OnToolsShowpolinomialkoefficients();
afx_msg void OnUpdateToolsShowpolinomialkoefficients(CCmdUI *pCmdUI);
afx_msg void OnFileSaveAs();
};
#ifndef _DEBUG // debug version in GpView.cpp
inline CGpDoc* CGpView::GetDocument() const
{ return reinterpret_cast<CGpDoc*>(m_pDocument); }
#endif
Листинг
5.1.
Функция перехода от системных координат к логическим координатам:
SDPoint CGpView::SysToLog(CPoint SysPoint)
{
CRect cr;
GetClientRect(&cr);
SDPoint Res;
Res.x = (static_cast<double>(SysPoint.x) - static_cast<double>(cr.right)/2)/ScaleXY - CameraPoint.x;
Res.y = (static_cast<double>(cr.bottom)/2 - static_cast<double>(SysPoint.y))/ScaleXY - CameraPoint.y;
return Res;
}Функция перехода от логических координат к системным координатам:
CPoint CGpView::LogToSys(double xl, double yl)
{
CRect cr;
GetClientRect(&cr);
CPoint Res;
Res.x = static_cast<int>((xl + CameraPoint.x)*ScaleXY + cr.right/2);
Res.y = static_cast<int>(-(yl + CameraPoint.y)*ScaleXY + cr.bottom/2);
return Res;
}CameraPoint - переменная для хранения координат точки наблюдения типа SDPoint. Функция GetClientRect(&cr) используется для получения клиентского прямоугольника. ScaleXY - переменная типа int, которая хранит масштаб (число пикселей в логической единице). Ее значение может быть задано произвольно, а может быть связано с характеристиками монитора с помощью соответствующих функций (например, int GetDeviceCaps(HDC hdc, int nIndex)) . Это основные функции, которые обеспечивают правильную работу программы в дальнейшем.