|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгоритмы симметричного шифрования. Часть 3. Алгоритмы Rijndael и RC6
Алгоритм Rijndael
Предварительные математические понятия
Практически все операции Rijndael определяются на уровне байта. Байты можно рассматривать как элементы конечного поля GF (28). Некоторые операции определены в терминах четырехбайтных слов. Введем основные математические понятия, необходимые для обсуждения алгоритма.
Поле GF(2^8)
Элементы конечного поля могут быть представлены несколькими различными способами. Для любой степени простого числа существует единственное конечное поле, поэтому все представления GF (28) являются изоморфными. Несмотря на подобную эквивалентность, представление влияет на сложность реализации. Выберем классическое полиномиальное представление.
Байт b, состоящий из битов b7, b6, b5, b4, b3, b2, b1, b0, представляется в виде полинома с коэффициентами из {0, 1}:
b7х7 + b6х6 + b5х5 + b4х4 + b3х3 + b2х2 + b1х1 + b0
Пример: байт с шестнадцатеричным значением ' 57 ' (двоичное 01010111 ) соответствует полиному
х6 + х4 + х2 + х + 1
Сложение
В полиномиальном представлении сумма двух элементов является полиномом с коэффициентами, которые равны сумме по модулю 2 (т.е. 1 + 1 = 0 ) коэффициентов слагаемых.
Пример: '57' + '83' = 'DA' или в полиномиальной нотации:
(х6 + х4 + х2 + х + 1) + (х7 + х + 1) = х7 + х6 + х4 + х2
В бинарной нотации мы имеем: 01010111 + 10000011 = 11011010.
Очевидно, что сложение соответствует простому XOR (обозначается как  )
на уровне байта.
)
на уровне байта.
Выполнены все необходимые условия Абелевой группы: операция сложения (каждой паре элементов сопоставляется третий элемент группы, называемый их суммой), ассоциативность, нулевой элемент (' 00 '), обратный элемент (относительно операции сложения) и коммутативность.
Умножение
В полиномиальном представлении умножение в GF (28) соответствует умножению полиномов по модулю неприводимого двоичного полинома степени 8. Полином является неприводимым, если он не имеет делителей, кроме 1 и самого себя. Для Rijndael такой полином называется m(x) и определяется следующим образом:
m(x) = x8 + x4 + x3 + x + 1
или ' 11B ' в шестнадцатеричном представлении.
Пример: 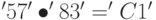
Или
| (x6 + x4 + x2 + х + 1) (x7 + х + 1) = |
| = x13 + x11 + x9 + x8 + x7 + x7 + x5 + x3 + x2 + x + x6 + x4 + x2 + х + 1 = |
| = x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1 |
(x8 + x4 + x3 + х + 1) (x5 + x3) + x7 + x6 + 1 = x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 +1
Следовательно,
x13 + x11 + x9 + x8 + x6 + x5 + x4 + x8 + 1 mod (x8 + x4 + x3 + х + 1) = x7 + x6 + 1
Ясно, что результат является двоичным полиномом не выше 8 степени. В отличие от сложения, простой операции умножения на уровне байтов не существует.
Умножение, определенное выше, является ассоциативным, и существует единичный элемент (' 01 '). Для любого двоичного полинома b(x) не выше 8-й степени можно использовать расширенный алгоритм Евклида для вычисления полиномов a(x) и c(x) таких, что
b(x) a(x) + m(x) c(x) = 1
Следовательно,
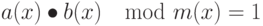
или
b-1(x) = a(x) mod m(x)
Более того, можно показать, что
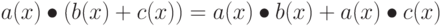
Из всего этого следует, что множество из 256 возможных значений байта образует конечное поле GF (28) c XOR в качестве сложения и умножением, определенным выше.
Умножение на х
Если умножить b(x) на полином х, мы будем иметь:
b7x8 + b6x7 + b5x6 + b4x5 + b3x4 + b2x3 + b1x2 + b0x
 получается понижением предыдущего результата по модулю m(x).
Если b7 = 0, то данное понижение является тождественной операцией.
Если b7 = 1, m(x) следует вычесть (т.е. XORed). Из этого следует, что
умножение на х может быть реализовано на уровне байта как левый сдвиг
и последующий побитовый XOR c ' 1B '. Данная операция обозначается как b = xtime (a).
получается понижением предыдущего результата по модулю m(x).
Если b7 = 0, то данное понижение является тождественной операцией.
Если b7 = 1, m(x) следует вычесть (т.е. XORed). Из этого следует, что
умножение на х может быть реализовано на уровне байта как левый сдвиг
и последующий побитовый XOR c ' 1B '. Данная операция обозначается как b = xtime (a).
Полиномы с коэффициентами из GF
Полиномы могут быть определены с коэффициентами из GF(28). В этом случае четырехбайтный вектор соответствует полиному степени 4.
Полиномы могут быть сложены простым сложением соответствующих коэффициентов. Как сложение в GF(28) является побитовым XOR, так и сложение двух векторов является простым побитовым XOR.
Умножение представляет собой более сложное действие. Предположим, что мы имеем два полинома в GF(28).
a(x) = a3x3 + a2x2 + a1x + a0 b(x) = b3x3 + b2x2 + b1x + b0
c(x) = a(x) b(x) определяется следующим образом:
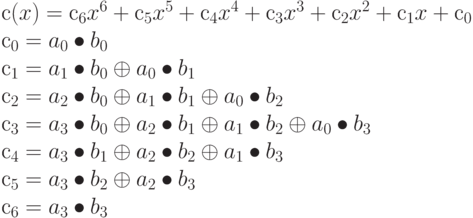
Ясно, что в таком виде с(х) не может быть представлен четырехбайтным вектором. Понижая с(х) по модулю полинома 4-й степени, результат может быть полиномом степени ниже 4. В Rijndael это сделано с помощью полинома
M(x) = x4 + 1
так как
xj mod (x4 + 1) = xj mod 4
Модуль, получаемый из а(х) и b(x), обозначаемый 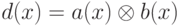 ,
получается следующим образом:
,
получается следующим образом:
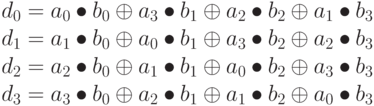
Операция, состоящая из умножения фиксированного полинома а(х), может быть записана как умножение матрицы, где матрица является циклической. Мы имеем
Замечание: х4 + 1 не является несократимым полиномом в GF (28), следовательно, умножение на фиксированный полином необязательно обратимо. В алгоритме Rijndael выбран фиксированный полином, который имеет обратный.
Умножение на х
При умножении b(x) на полином х будем иметь:
b3x4 + b2x3 + b1x2 + b0x
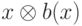 получается понижением предыдущего результата по модулю 1 + х4.
получается понижением предыдущего результата по модулю 1 + х4.
Это дает
b2x3 + b1x2 + b0x + b3
Умножение на х эквивалентно умножению на матрицу, как описано выше со всеми ai = '00' за исключением а1 = '01'. Имеем:
Следовательно, умножение на х соответствует циклическому сдвигу байтов внутри вектора.
Обоснование разработки
При разработке алгоритма учитывались следующие три критерия:
- противодействие всем известным атакам;
- скорость и компактность кода для широкого круга платформ;
- простота разработки.
В большинстве алгоритмов шифрования преобразование каждого раунда имеет структуру сети Фейштеля. В этом случае обычно часть битов в каждом промежуточном состоянии просто перемещается без изменения в другую половину. Преобразование раунда алгоритма Rijndael не имеет структуру сети Фейштеля. Вместо этого преобразование каждого раунда состоит из четырех различных преобразований, называемых слоями.
Каждый слой разрабатывался с учетом противодействия линейному и дифференциальному криптоанализу. В основу каждого слоя положена своя собственная функция:
- Нелинейный слой состоит из параллельного применения S-boxes для оптимизации нелинейных свойств в наихудшем случае.
- Слой линейного перемешивания строк гарантирует высокую степень диффузии для нескольких раундов.
- Слой линейного перемешивания столбцов также гарантирует высокую степень диффузии для нескольких раундов.
- Дополнительный слой ключа состоит из простого XOR промежуточного состояния с ключом раунда.
Перед первым раундом применяется дополнительное забеливание с использованием ключа. Причина этого состоит в следующем. Любой слой после последнего или до первого добавления ключа может быть просто снят без знания ключа и тем самым не добавляет безопасности в алгоритм (например, начальная и конечная перестановки в DES). Начальное или конечное добавление ключа применяется также в некоторых других алгоритмах, например IDEA, SAFER и Blowfish.
Для того чтобы сделать структуру алгоритма более простой, слой линейного перемешивания последнего раунда отличается от слоя перемешивания других раундов. Можно показать, что это в любом случае не повышает и не понижает безопасность. Это аналогично отсутствию операции swap в последнем раунде DES.



