Математические модели РЭС на метауровне
16.1. Математические модели аналоговой РЭА
Использование основных положений схемотехнического моделирования для проектирования сложной аналоговой РЭА на метауровне оказывается затруднительным. Это связано с чрезмерно большими размерностями задач. Для их решения необходимы упрощения. Основой снижения размерности задач является макромоделирование. Часто используют ряд дополнительных упрощений и допущений. Главные из них формулируются следующим образом.
- Однонаправленность в передаче сигналов, т. е. использование макромоделей, в которых отсутствует влияние выходных переменных на состояние входных цепей.
- Отсутствие влияния нагрузки на параметры и состояние моделируемых систем.
- Использование вместо фазовых переменных двух типов (напряжение и ток) переменных одного типа, называемых сигналами. При этом компонентные уравнения элемента представляют собой уравнения связи сигналов на входах и выходах этого элемента.
- Линейность моделей инерционных элементов.
Перечисленные допущения характерны для функционального моделирования, широко применяемого для анализа систем автоматического управления. Элементы (звенья) систем при функциональном моделировании делят на три группы:
- линейные безынерционные звенья для отображения таких функций, как повторение, инвертирование, чистое запаздывание, идеальное усиление, суммирование сигналов;
- нелинейные безынерционные звенья для отображения различных нелинейных преобразований сигналов (ограничение, детектирование, модуляция и т. п.);
- линейные инерционные звенья для выполнения дифференцирования, интегрирования, фильтрации сигналов.
Инерционные элементы представлены отношениями преобразованных по Лапласу или Фурье выходных и входных фазовых переменных. При анализе во временной области применяют преобразование Лапласа — модель инерционного элемента с одним входом и одним выходом есть передаточная функция; а при анализе в частотной области (преобразование Фурье) модель элемента есть выражения амплитудно-частотной и частотно-фазовой характеристик. При наличии нескольких входов и выходов ММ элемента представляется матрицей передаточных функций или частотных характеристик.
Допущения, принимаемые при функциональном моделировании, существенно упрощают алгоритмы получения математических моделей систем (ММС) из математических моделей элементов (ММЭ).
Математическая модель системы представляет собой совокупность ММЭ, входящих в систему, при отождествлении переменных, относящихся к соединяемым входам и выходам.
16.2. Математические модели логических схем цифровой РЭА
На функционально-логическом уровне необходим ряд положений, которые упрощают модели устройств. Это позволяет анализировать более сложные объекты по сравнению с объектами, анализируемыми на схемотехническом уровне. Часть используемых положений аналогична положениям, принимаемым для моделирования аналоговой РЭА.
Во-первых, это положение о представлении состояний объектов с помощью однотипных фазовых переменных (обычно напряжений), называемых сигналами.
Во-вторых, не учитывается влияние нагрузки на функционирование элементов-источников.
В-третьих, принимается допущение об однонаправленности, т. е. о возможности передачи сигналов через элемент только в одном направлении — от входов к выходам.
Дополнительно к этим положениям при моделировании цифровой РЭА принимается положение о дискретизации переменных, их значения могут принадлежать только заданному конечному множеству — алфавиту, например двоичному алфавиту {0,1}.
Моделирование цифровой РЭА возможно с различной степенью детализации. На логическом ( вентильном ) подуровне функционально-логического проектирования в качестве элементов аппаратуры рассматривают простые схемы типа вентилей, на регистровом подуровне элементами могут быть как отдельные вентили, так и любые более сложные сочетания простых схем, например регистры, счетчики, дешифраторы, сумматоры, арифметико-логические устройства и т. п.
Рассмотрим математические модели элементов на логическом подуровне. Для одновыходных комбинационных элементов ММ представляет собой выражение (в общем случае алгоритм), позволяющее по значениям входных переменных (значениям входов) в заданный момент времени t вычислить значение выходной переменной (значение выхода) в момент времени t + t3t где t3 — задержка сигнала в элементе. Такую модель элемента называют асинхронной. При t3 = 0 модель элемента называют синхронной. Модель многовыходного элемента должна включать в себя алгоритм вычисления задержек и значений всех выходных сигналов.
Для элементов последовательностных схем (элементов с памятью) используют модели, в которых аргументами выходных переменных уj могут быть как входные ui, так и внутренние uk переменные. Вектор внутренних переменных V отражает состояние элемента (состояние его памяти).
Объединение моделей элементов в общую математическую модель системы выполняется на основе вышеперечисленных допущений отождествлением переменных на соединяемых входах и выходах элементов.
16.3. Имитационные модели
Все развитие науки связано с созданием и изучением моделей реальных систем, процессов и явлений. Язык науки требует, чтобы изучаемое явление (система-процесс) было описано на точном уровне, не допускающем принципиальных разночтений. Наиболее точны математические модели. На другом конце шкалы точности — текстовые модели, использующие, по возможности, однозначные понятия. Имитационные модели находятся между этими крайними точками шкалы точности. В этой науке создаются и используются специальные приемы воспроизведения процессов, протекающих в реальных объектах, в тех моделях этих объектов, которые реализуются в ЭВМ.
Имитационное моделирование, как правило, связано с моделированием динамических объектов, процессов и явлений. Изменения ситуаций во времени — тот феномен, который изучается с помощью имитационных моделей. В результате могут быть получены новые знания или выработаны разного рода решения. Например, диспетчер на железной дороге, смотрящий на табло, по которому в условном виде перемещаются поезда и вагоны на сортировочной станции, имеет дело с отображающей моделью. Но если такое табло находится в учебном центре, где обучают будущих диспетчеров, то процессы, отражаемые на табло, лишь имитируют реальность. И в этом случае речь идет об имитационном моделировании.
Появление ЭВМ дало мощный толчок для развития имитационного моделирования. Существуют два типа имитационных моделей: моделирование по времени и моделирование по событиям [38].
В первом случае в ЭВМ имеется датчик временных интервалов, разбивающий непрерывную шкалу времени на участки стандартной длины. Длина этих участков определяется спецификой моделируемого явления. Если, например, надо воспроизвести в машине процессы, протекающие в период движения снаряда в стволе оружия, то интервалы должны составлять тысячные доли секунды. Если же на ЭВМ моделируется процесс оседания на дно водоема твердых частиц, то интервалы моделирования могут соответствовать часам или даже суткам.
Для имитационного моделирования разработаны специальные программные средства: специализированные языки программирования (наиболее распространенный из них — СИМУЛА) и специализированные пакеты прикладных программ.
Реальные сложные системы функционируют в условиях действия большого количества случайных возмущающих факторов, приводящих к нарушению нормального хода работы. Источниками возмущающих факторов являются воздействия внешней среды, а также различные отклонения, возникающие внутри системы. Под действием случайных факторов производительность, время выполнения планового задания и другие технико-экономические показатели не только подвергаются рассеянию, но и могут получить смещение своих средних значений. Поэтому оценка только по средним значениям приблизительна.
При моделировании на ЭВМ технологического процесса происходит воспроизведение явлений с сохранением их логической структуры и расположения во времени. Это позволяет получать наиболее точные характеристики процесса проектирования (техническую производительность, время проведения отдельных технологических операций и т. д.).
Цель моделирования технологического процесса заключается в проектном расчете технической производительности и других показателей экономической эффективности с учетом заданного варианта структуры каждой операции технологического процесса, надежности оборудования и инструмента, различных событий, возникающих в процессе проведения операций.
Результаты моделирования используются для повышения качества принимаемых значений на этапе проектирования операций и подготовки управляющих программ, а также позволяют исследовать степень влияния надежности отдельных операций, числа и вида инструментов-дублеров, размера партии изделий на их выходные показатели. Таким образом, моделирование технологического процесса выполняется для решения следующих задач:
- прогнозирование основных выходных характеристик изделия при заданном варианте структуры технологического процесса, времени его проведения, технической производительности, длительности простоев из-за отказов инструментов и оборудования, среднего числа отказов и др.;
- получение закона распределения времени при выполнении планового задания, статистических характеристик и других показателей экономической эффективности;
- использование результатов моделирования для выбора оптимального варианта структуры технологического процесса;
- исследование вариантов структуры процесса с помощью разработанной имитационной модели.
Математическая модель технологического процесса строится с учетом заданного варианта его структуры, заданной компоновки оборудования, надежности элементов и их взаимосвязи в процессе обработки.
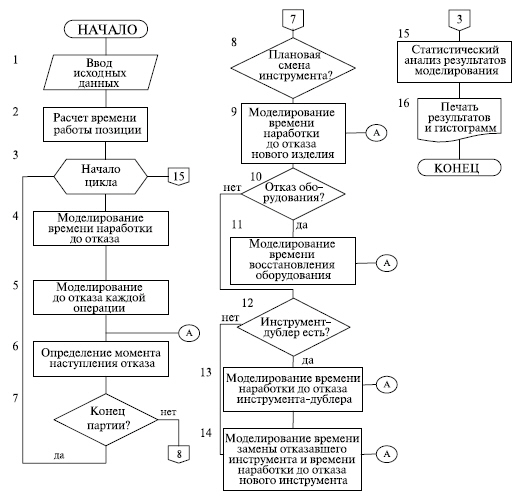
В основу моделирования технологического процесса положена структура каждой из его операций, определяющая, какие переходы, на какой позиции и в какой последовательности выполняются, какие инструментыдублеры используются и т. д.
Процесс изготовления РЭС является дискретным стохастическим процессом. Его дискретность заключается в том, что элементарные операции (переходы, мероприятия восстановления работоспособности и др.) выполняются не мгновенно, а имеют определенную длительность, причем следующая процедура выполняется только после полного окончания предыдущей.
В процессе изготовления принимает участие большое число элементов (инструменты, оборудование), которые в случайные моменты времени могут выходить из строя, требуя замены или ремонта. Это приводит к нарушению нормального хода процесса. Величины, оценивающие появление отказов и затраты времени на выполнение восстановительных работ, носят случайный характер. Случайными являются: время работы оборудования до отказа, время работы каждого инструмента до отказа, время бесперебойной работы между последовательными отказами, время восстановления работоспособности, суммарное время изготовления РЭС, техническая производительность и т. д.
Имитационную модель проверяют на чувствительность, т.е. определяют значимость влияния возможных отклонений в пределах заданной точности (допуска) постоянных параметров x1, ..., xk, входящих в модель, на результат моделирования Р ( рис. 16.1). С помощью имитационной модели можно, например, определить показатели качества изделия, время проведения процесса изготовления, собственные потери времени из-за отказов инструментов и техническую производительность. Таким образом, имитационная модель и моделирование технологического процесса позволяют воспроизводить последовательную или параллельно-последовательную схему ( рис. 16.1), где вi — величина постоянных ограничений в правой части; t — время проведения операции; S — вектор входных параметров; v — управляющие воздействия.
Величины вi могут колебаться в пределах вi min – вi max, что обуславливается видом ограничения, технологическими характеристиками процесса, требованиями к точности и качеству изготавливаемой продукции и т.д. Используя подход имитационного моделирования, находят отклонения от оптимальных параметров процесса и целевой функции, полученных по усредненным данным, значений этих же параметров и величины целевой функции, найденных при условии, что постоянные вi в ограничениях модели принимают свои крайние значения, каждое из которых имеет два уровня: вi min и вi max.
Определив с помощью математической модели оптимальные параметры обработки и величину целевой функции для каждого случая предельных отклонений колебаний постоянных вi, оценивают степень расхождения полученных характеристик с соответствующими значениями усредненного варианта.
Определяют вероятность того, что 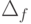 и
и 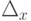 (10.11) находятся в пределах заданной точности
(10.11) находятся в пределах заданной точности 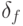 и
и 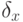 , т. е.
, т. е.
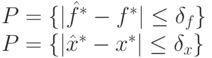
Чтобы найти оптимальные режимы операций и экстремум целевой функции с заданной точностью и надежностью, необходимо обеспечить выполнение следующих условий:
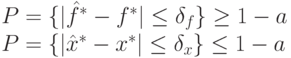
где найденные режимы операций и значение целевой функции будут находиться в заданных пределах с достоверностью (1 – а).
Для сокращения числа вариантов нужно, в первую очередь, учитывать активные ограничения в усредненном варианте и рассматривать вариацию правой части ограничений вi только для их активной части.
Контрольные вопросы и упражнения
- В чем заключается сложность проектирования аналоговой РЭА?
- Что является основой снижения размерности задач?
- Как формулируются упрощения и допущения при снижении размерности задач?
- В чем сущность функционального моделирования?
- Назовите группы систем при функциональном проектировании.
- Что представляет собой ММ системы?
- Какая модель называется синхронной?
- Какая модель называется асинхронной?
- Какие функции выполняют линейные инерционные звенья?
- Какие функции выполняют нелинейные инерционные звенья?
- Какие функции выполняют нелинейные безынерционные звенья?
- Что называют имитационным моделированием?
- Что называют чувствительностью имитационной модели?