Методы автоматизированного проектирования конструкции и технологического процесса различного уровня иерархии
12.1. Иерархическая структура проектных спецификаций и иерархические уровни проектирования
Выполнение проектных операций и процедур в САПР основано на оперировании математических моделей (ММ). С их помощью прогнозируются характеристики и оцениваются возможности предложенных вариантов схем и конструкций, проверяется соответствие предъявляемым требованиям, проводится оптимизация параметров, разрабатывается техническая документация и т. п.
В САПР для каждого иерархического уровня сформулированы основные положения математического моделирования, выбран и развит соответствующий математический аппарат, получены типовые ММ элементов проектируемых объектов, формализованы методы получения и анализа математических моделей систем. Сложность задач проектирования и противоречивость требований высокой точности, полноты и малой трудоемкости анализа обусловливают целесообразность компромиссного удовлетворения этих требований с помощью соответствующего выбора моделей. Это обстоятельство приводит к расширению множества используемых моделей и развитию алгоритмов адаптивного моделирования.
При использовании блочно-иерархического подхода к проектированию представления о проектируемой системе разделяют на иерархические уровни. На верхнем уровне используют наименее детализированное представление, отражающее только самые общие черты и особенности проектируемой системы. На следующих уровнях степень подробности описания возрастает, при этом рассматривают уже отдельные блоки системы, но с учетом воздействий на каждый из них его соседей. Такой подход позволяет на каждом иерархическом уровне формулировать задачи приемлемой сложности, поддающиеся решению с помощью имеющихся средств проектирования. Разбиение на уровни должно быть таким, чтобы документация на блок любого уровня была обозрима и воспринимаема одним человеком [71, 53, 15].
Другими словами, блочно-иерархический подход есть декомпозиционный подход (его называют также диакоптическим), который основан на разбиении сложной задачи большой размерности на последовательно и (или) параллельно решаемые группы задач малой размерности, что существенно сокращает требования к используемым вычислительным ресурсам или время решения задач.
Можно говорить об иерархических уровнях не только спецификаций, но и проектирования, понимая под каждым из них совокупность спецификаций некоторого иерархического уровня совместно с постановками задач, методами получения описаний и решения возникающих проектных задач.
Список иерархических уровней в каждом приложении может быть специфичным, но для большинства приложений характерно следующее наиболее крупное выделение уровней [33, 38, 55]:
- метауровень, на котором решают наиболее общие задачи проектирования систем, машин и процессов. Результаты проектирования представляют в виде структурных схем, генеральных планов, схем размещения оборудования, диаграмм потоков данных и т. д.;
- макроуровень, на котором проектируют отдельные устройства, узлы машин и приборов. Результаты представляют в виде функциональных, принципиальных и кинематических схем, сборочных чертежей и т. п.;
- микроуровень, на котором проектируют отдельные детали и элементы машин и приборов.
В каждом приложении число выделяемых уровней и их наименования могут быть различными. Так, в радиоэлектронике микроуровень часто называют компонентным, макроуровень — схемотехническим. Между схемотехническим и системным уровнями вводят уровень, называемый функционально-логическим. В вычислительной технике системный уровень подразделяют на уровни проектирования ЭВМ (вычислительных систем) и вычислительных сетей. В машиностроении имеются уровни деталей, узлов, машин, комплексов.
В зависимости от последовательности решения задач иерархических уровней различают нисходящее проектирование, восходящее и смешанное проектирование (стили проектирования). Последовательность решения задач от нижних уровней к верхним характеризует восходящее проектирование, обратная последовательность приводит к нисходящему проектированию, в смешанном стиле имеются элементы как восходящего, так и нисходящего проектирования. В большинстве случаев для сложных систем предпочитают нисходящее проектирование. При наличии заранее спроектированных составных блоков (устройств) можно говорить о смешанном проектировании.
Неопределенность и нечеткость исходных данных при нисходящем проектировании (так как еще не спроектированы компоненты) или исходных требований при восходящем проектировании (поскольку ТЗ имеется на всю систему, а не на ее части) обусловливают необходимость прогнозирования недостающих данных с последующим их уточнением, т. е. последовательного приближения к окончательному решению (итерационность проектирования).
Наряду с декомпозицией описаний на иерархические уровни применяют разделение представлений о проектируемых объектах на аспекты.
Аспект описания (страта) — описание системы или ее алгоритмического (разработка алгоритмов и программного обеспечения) и технологического (разработка технологических процессов) проектирования. Примерами страт в случае САПР могут служить также рассмотренные ранее виды обеспечения автоматизированного проектирования.
12.2. Требования к математическим моделям и их классификация
Под математической моделью (ММ) конструкции, технологического процесса и его элементов понимают систему математических соотношений, описывающих с требуемой точностью изучаемый объект и его поведение в производственных условиях. При построении математических моделей используют различные математические средства описания объекта — теорию множеств, теорию графов, теорию вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и т. д.
Выполнение проектных операций и процедур в САПР основано на оперировании математическими моделями (ММ). С их помощью прогнозируются характеристики и оцениваются возможности предложенных вариантов схем и конструкций, проверяется их соответствие предъявляемым требованиям, проводится оптимизация параметров, разрабатывается техническая документация и т. п.
В САПР для каждого иерархического уровня сформулированы основные положения математического моделирования — выбран и развит соответствующий математический аппарат, получены типовые ММ элементов проектируемых объектов, формализованы методы получения и анализа математических моделей систем. Сложность задач проектирования и противоречивость требований высокой точности, полноты и малой трудоемкости анализа обусловливают целесообразность компромиссного удовлетворения этих требований с помощью соответствующего выбора моделей. Это обстоятельство приводит к расширению множества используемых моделей и развитию алгоритмов адаптивного моделирования [32, 17, 27].
К математическим моделям предъявляют требования высокой точности, экономичности и универсальности. Экономичность математических моделей определяется затратами машинного времени (работы ЭВМ). Степень универсальности математических моделей зависит от возможности их использования для анализа большого числа технологических процессов и их элементов. Требования к точности, экономичности и степени универсальности математических моделей противоречивы. Поэтому необходимо иметь удачное компромиссное решение.
Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности и экономичности [77].
Адекватность. Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта. Пусть  — относительная погрешность модели по j -му выходному параметру:
— относительная погрешность модели по j -му выходному параметру:
 |
( 12.1) |
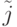 — j -й выходной параметр, рассчитанный с помощью модели; yj — тот же выходной параметр, существующий в моделируемом объекте.
— j -й выходной параметр, рассчитанный с помощью модели; yj — тот же выходной параметр, существующий в моделируемом объекте.Погрешность модели  по совокупности учитываемых выходных параметров оценивается одной из норм вектора
по совокупности учитываемых выходных параметров оценивается одной из норм вектора  .
.
Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельной допустимой погрешностью  , то можно в пространстве внешних параметров выделить область, в которой выполняется условие
, то можно в пространстве внешних параметров выделить область, в которой выполняется условие
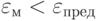 |
( 12.2) |
Эту область называют областью адекватности (ОА) модели. Возможно введение индивидуальных предельных значений  для каждого выходного параметра и определение ОА как области, в которой одновременно выполняются все m условий вида
для каждого выходного параметра и определение ОА как области, в которой одновременно выполняются все m условий вида  .
.
Определение областей адекватности для конкретных моделей — сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства внешних параметров. Определение ОА —более трудная задача, чем, например, задача параметрической оптимизации. Для моделей унифицированных элементов расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании различных систем. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.
В библиотеку моделей элементов наряду с алгоритмом, реализующим модель, и номинальными значениями параметров должны включаться граничные значения внешних параметров q'k и q''k, задающие область адекватности.
Универсальность. При определении ОА необходимо выбрать совокупность внешних параметров и совокупность выходных параметров уj, отражающих учитываемые в модели свойства. Типичными внешними параметрами при этом являются параметры нагрузки и внешних воздействий (электрических, механических, тепловых, радиационных и т. п.). Увеличение числа учитываемых внешних факторов расширяет применимость модели, но существенно удорожает работу по определению ОА. Выбор совокупности выходных параметров также неоднозначен, однако для большинства объектов число и перечень учитываемых свойств и соответствующих им выходных параметров сравнительно невелики, достаточно стабильны и составляют типовой набор выходных параметров. Например, для макромоделей логических элементов БИС такими выходными параметрами являются уровни выходного напряжения в состояниях логических "О" и "1", запасы помехоустойчивости, задержка распространения сигнала, рассеиваемая мощность.
Если адекватность характеризуется положением и размерами ОА, то универсальность модели определяется числом и составом учитываемых в модели внешних и выходных параметров.
Экономичность. Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации, а именно затратами машинного времени Тм и памяти Пм. Общие затраты Тм и Пм на выполнение в САПР какой-либо проектной процедуры зависят как от особенностей выбранных моделей, так и от методов решения.
В большинстве случаев при реализации численного метода происходят многократные обращения к модели элемента, входящего в состав моделируемого объекта. Тогда удобно экономичность модели элемента характеризовать затратами машинного времени при обращении к модели, а число обращений к модели должно учитываться при оценке экономичности метода решения.
Экономичность модели по затратам памяти оценивается объемом оперативной памяти, необходимой для реализации модели.
Требования широких областей адекватности, высокой степени универсальности, с одной стороны, и высокой экономичности — с другой, являются противоречивыми. Наилучшее компромиссное удовлетворение этих требований оказывается неодинаковым в различных применениях. Это обстоятельство обусловливает использование в САПР многих моделей для объектов одного и того же типа — различного рода макромоделей, многоуровневых, смешанных моделей и т. п.
