Шифрование, помехоустойчивое кодирование и сжатие информации

Цель лекции: познакомиться с принципами совместного использования шифрования, помехоустойчивого кодирования и сжатия информации для комплексной защиты информации в процессе ее передачи и хранения.

Проблемы передачи информации и их комплексное решение

В процессе передачи информации от источника к потребителю на информацию воздействуют различные неблагоприятные факторы. Криптографические методы защищают информацию только от одного вида разрушающих воздействий – от предумышленного разрушения или искажения информации. Однако на практике при передаче информации от абонента к абоненту возможны случайные помехи на линиях связи, ошибки и сбои аппаратуры, частичное разрушение носителей данных и т.д. Таким образом, в реальных системах связи существует проблема защиты информации от случайных воздействий.

В связи с появлением сетей передачи данных высокой пропускной способности и развитием мультимедиа-технологий возникает проблема шифрования больших объемов информации. Если раньше основным типом шифруемых и передаваемых сообщений было текстовое сообщение, то в ХХI веке криптографическая защита все чаще применяется при передаче цифровых видео- и речевых сообщений, карт местности, для организации видеоконференций. Именно поэтому в последнее время возникает проблема шифрования огромных информационных массивов. Для интерактивных систем типа телеконференций, организации аудио- или видеосвязи, такое шифрование должно осуществляться в реальном режиме времени и по возможности быть незаметным для пользователей.

Решение указанных проблем, в том числе и защита от несанкционированного доступа, может быть достигнуто при комплексном использовании достижений теории информации.

В принципе в теории информации выделяют три вида преобразования информации: криптографическое шифрование, помехоустойчивое кодирование и сжатие (или компрессия). В некоторых научных работах ХХ века все три вида преобразования информации называли кодированием: криптографическое кодирование, помехоустойчивое кодирование и эффективное кодирование (сжатие данных). Общим для всех трех видов преобразования является то, что информация каким-либо образом меняет форму представления, но не смысл. Отличия разных видов кодирования связаны с целью проводимых преобразований.

Так, целью криптографического преобразования является, как известно, защита от несанкционированного доступа, аутентификация и защита от преднамеренных изменений. Помехоустойчивое кодирование выполняется с целью защиты информации от случайных помех при передаче и хранении. Эффективное кодирование производится с целью минимизации объема передаваемых или хранимых данных.

На практике эти три вида преобразования информации обычно используются совместно. Так, например, некоторые программные пакеты перед шифрованием архивируют обрабатываемые данные. С другой стороны, реальные системы передачи информации, будь то локальные и глобальные сети передачи данных, или компьютерные носители информации (CD или DVD-диски) всегда имеют в составе системы защиты информации средства контроля и коррекции случайных ошибок.

Таким образом, криптографическое шифрование, помехоустойчивое кодирование и сжатие отчасти дополняют друг друга и их комплексное использование помогает эффективно использовать каналы связи для надежной защиты передаваемой информации.

Для того, чтобы более эффективно использовать на практике криптографические методы защиты информации, рассмотрим основные положения теорий помехоустойчивого и эффективного кодирования, используемые в системах защиты информации.

Помехоустойчивое кодирование

Как уже отмечалось, вопросы криптографического преобразования информации тесно связаны с вопросами помехоустойчивого кодирования сообщений. Это обусловлено, с одной стороны (теоретической), тем, что и при криптографическом шифровании, и при помехоустойчивом кодировании используются одни и те же законы теории информации. С другой стороны (практической) процессы накопления, хранения и передачи информации протекают в условиях воздействия помех, способных исказить хранимые и обрабатываемые данные. Это обуславливает актуальность разработки и использования методов, позволяющих обнаруживать и корректировать подобные ошибки. С математической точки зрения задача сводится к синтезу так называемых помехоустойчивых кодов.

Аналогично понятию шифра в криптографии при обсуждении помехоустойчивого кодирования и вопросов сжатия сообщений вводят понятие кода. Вообще кодом называется совокупность знаков, а также система правил, позволяющая представлять информацию в виде набора таких знаков. Кодовым словом называют любой ряд допустимых знаков. Например, двоичное число 1100 можно считать двоичным 4-разрядным кодовым словом.

Общая идея помехоустойчивого кодирования состоит в том, что из всех возможных кодовых слов считаются допустимыми не все, а лишь некоторые из них. Например, в коде с контролем по четности считаются допустимыми лишь слова с четным числом единиц. Ошибка превращает допустимое слово в недопустимое и поэтому обнаруживается.

Помехоустойчивые коды делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.

Блоковые коды характеризуются так называемым минимальным кодовым расстоянием. Вообще, расстоянием по Хэммингу (по имени американского математика Р.У. Хэмминга) между двумя кодовыми словами называется число разрядов, в которых они различны. При этом в качестве минимального кодового расстояния выбирается наименьшее из всех расстояний по Хэммингу для любых пар различных кодовых слов, образующих код.

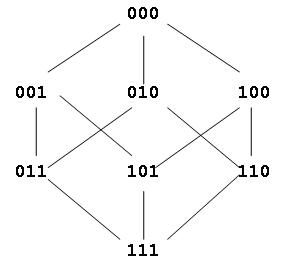
Например, пусть мы используем только трехразрядные двоичные слова. Всего таких кодовых слов может быть восемь. Те кодовые слова, которые отличаются только на одну единицу, называются соседними. Например, кодовые слова 101 и 111 – соседние, так как отличаются только средним разрядом, а слова 101 и 110 – не соседние, так как у них отличаются два последних разряда. Изобразим все трехразрядные двоичные комбинации и соединим линией соседние кодовые слова. Тогда мы получим схему, как на рис. 14.1. Минимальное кодовое расстояние между словами обычного, не помехоустойчивого кода равно единице.

Рис. 14.1. Трехразрядные двоичные кодовые слова

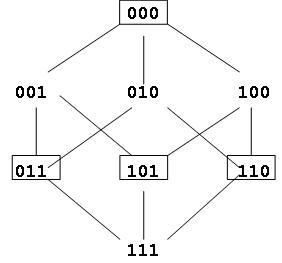
В случае использования всех трехразрядных двоичных слов для передачи сообщений все они будут считаться допустимыми. Применим контроль по условию четности. Тогда допустимыми будут только выделенные рамками слова с четным числом единиц (см. рис. 14.2).

Рис. 14.2. Допустимые трехразрядные кодовые слова при контроле по четности