|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Криптография с использованием эллиптических кривых
Математические понятия
Преимущество подхода на основе эллиптических кривых в сравнении с задачей факторизации числа, используемой в RSA, или задачей целочисленного логарифмирования, применяемой в алгоритме Диффи-Хеллмана и в DSS, заключается в том, что в данном случае обеспечивается эквивалентная защита при меньшей длине ключа.
В общем случае уравнение эллиптической кривой Е имеет вид:
y2 + axy + by = x3 + cx2 + dx + e
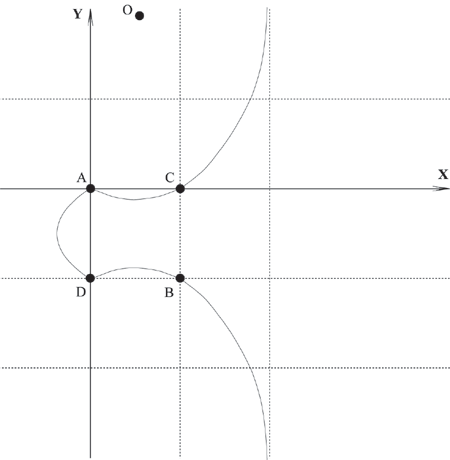
В качестве примера рассмотрим эллиптическую кривую Е, уравнение которой имеет вид:
y2 + y = x3 - x2
На этой кривой лежат только четыре точки, координаты которых являются целыми числами. Это точки
А (0, 0), В (1, -1), С (1, 0) и D (0, -1)
Для определения операции сложения для точек на эллиптической кривой сделаем следующие предположения:
- На плоскости существует бесконечно удаленная точка
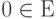 , в которой сходятся все вертикальные прямые.
, в которой сходятся все вертикальные прямые. - Будем считать, что касательная к кривой пересекает точку касания два раза.
- Если три точки эллиптической кривой лежат на прямой линии, то их сумма есть 0.
Введем следующие правила сложения точек на эллиптической кривой:
- Точка 0 выступает в роли нулевого элемента. Так, 0 = -0 и для любой точки Р на эллиптической кривой Р + 0 = Р.
- Вертикальная линия пересекает кривую в двух точках с одной и той же координатой х - скажем, S = (x, y) и T = (x, -y). Эта прямая пересекает кривую и в бесконечно удаленной точке. Поэтому Р1 + Р2 + 0 = 0 и Р1 = -Р2.
- Чтобы сложить две точки P и Q (см. рисунок 11.2) с разными координатами х, следует провести через эти точки прямую и найти точку пересечения ее с эллиптической кривой. Если прямая не является касательной к кривой в точках P или Q, то существует только одна такая точка, обозначим ее S. Согласно нашему предположению
P + Q + S = О
Следовательно,
P + Q = -S или P + Q = T
Если прямая является касательной к кривой в какой-либо из точек P или Q, то в этом случае следует положить S = P или S = Q соответственно.
- Чтобы удвоить точку Q, следует провести касательную в точке Q и найти другую точку пересечения S с эллиптической кривой. Тогда Q + Q = 2 x Q = -S.
Введенная таким образом операция сложения подчиняется всем обычным правилам сложения, в частности коммутативному и ассоциативному законам. Умножение точки Р эллиптической кривой на положительное число k определяется как сумма k точек Р.
В криптографии с использованием эллиптических кривых все значения вычисляются по модулю р, где р является простым числом. Элементами данной эллиптической кривой являются пары неотрицательных целых чисел, которые меньше р и удовлетворяют частному виду эллиптической кривой:
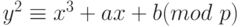
Такую кривую будем обозначать Ep (a,b). При этом числа а и b должны быть меньше р и должны удовлетворять условию 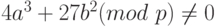 . Множество точек на эллиптической кривой вычисляется следующим образом.
. Множество точек на эллиптической кривой вычисляется следующим образом.
- Для каждого такого значения х, что 0 <= х <= р, вычисляется x3 + ax + b (mod p).
- Для каждого из полученных на предыдущем шаге значений выясняется, имеет ли это значение квадратный корень по модулю р. Если нет, то в Ep (a,b) нет точек с этим значением х. Если корень существует, имеется два значения y, соответствующих операции извлечения квадратного корня (исключением является случай, когда единственным значением оказывается y = 0 ). Эти значения (x,y) и будут точками Ep (a,b).
Множество точек Ep (a,b) обладает следующими свойствами:
- Р + 0 = Р
- Если Р = (x,y), то Р + (x,-y) = 0. Точка (x,-y) является отрицательным значением точки Р и обозначается -Р. Заметим, что (x,-y) лежит на эллиптической кривой и принадлежит Ep (a,b).
- Если Р = (x1,y1) и Q = (x2,y2), где
 , то P + Q = (x3,y3) определяется по следующим формулам:
, то P + Q = (x3,y3) определяется по следующим формулам: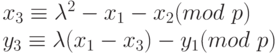
где
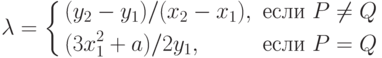
Число  есть угловой коэффициент секущей, проведенной через точки P = (x1, y1) и Q = (x2, y2). При P = Q секущая превращается в касательную, чем и объясняется наличие двух формул для вычисления
есть угловой коэффициент секущей, проведенной через точки P = (x1, y1) и Q = (x2, y2). При P = Q секущая превращается в касательную, чем и объясняется наличие двух формул для вычисления 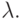
Задача, которую должен решить в этом случае атакующий, есть своего рода задача "дискретного логарифмирования на эллиптической кривой", и формулируется она следующим образом. Даны точки P и Q на эллиптической кривой Ep (a,b). Необходимо найти коэффициент k < p такой, что
P = k x Q
Относительно легко вычислить P по данным k и Q, но довольно трудно вычислить k, зная P и Q.
Рассмотрим три способа использования эллиптических кривых в криптографии.