|
есть желание заново пройти курс "Тестирование в современном высшем образовании"
|
Шкалирование и интерпретация результатов тестирования
6.1. Основные шкалы и принципы
Разработка тестов и тестирование всегда приводит к необходимости выбора шкалы, по которой будет оцениваться качество выполнения теста. Классическая шкала – мало дифференцирующая, с большой долей субъективизма.
Первичная информация при тестировании обучаемого – его первичные ("сырые") баллы. Они наглядны, просты, но существенно зависят, например, от трудности заданий. Необходима более объективная шкала оценок подготовленности обучающихся, необходимо подтверждение уровня обученности на различных тестах, с заранее определенным уровнем трудности заданий.
Также следует избавиться и от нелинейности первичных баллов по отношению к уровню подготовленности.
Пример. Шкала оценок в школе позволяет заключить лишь то, что ученик Иванов учится лучше ученика Петрова. Каковы их различия, успехи, усилия и т.д.? – Такая шкала ответа на подобные вопросы не дает. Аналогично, первичные баллы лишь упорядочивают участников тестирования.
В таких порядковых шкалах основные статистики – медиана, квантили и ранговая корреляция.
Позиционирование испытуемых на числовой оси согласно результатам испытаний осуществляется различным образом. Поэтому используются различные типы шкал оценок, например, следующие.
Шкала итоговой оценки – шкала, определяемая по минимальной и максимальной оценкам (баллам), это линейное преобразование отрезка от минимальной до максимальной оценки; например, шкала 100-балльная.
Шкала нормативная – шкала, вводимая на основе справедливости гипотезы о нормальном законе распределения баллов; например, перевод в нормативную шкалу предполагает, что знания испытуемых в их произвольной выборке подчиняются нормальному закону распределения, следовательно, равным отрезкам под кривой нормального распределения соответствуют равные количества верных ответов.
Шкала порядковая, качественная, отношений – шкала для введения отношений порядка в совокупность шкалируемых объектов, систем и выполнения всех преобразований, не нарушающих это правило порядка; например, шкала оценок в средней школе – 2, 3, 4, 5 и в высшей школе – "неудовлетворительно", "удовлетворительно", "хорошо", "отлично".
Шкала номинальная (наименований) используется экспертами при классификации эмпирических объектов измерения. Такая шкала применяется тогда, когда педагогическое измерение группирует обучающихся без установления порядка следования групп; например, деление студентов на группы сдавших и не сдавших зачет.
Пример. Если тестируемый за правильный (неправильный) ответ по заданию получает 1 (0), то результаты тестирования представляются в номинальной шкале.
Шкала интервальная – шкала, в которой допустимы лишь линейные функции преобразования, и в которых часто нельзя отметить ни начало, ни конец, ни единицу измерения (градацию) шкалы; например, температурные шкалы Фаренгейта и Цельсия связаны зависимостью: С = 5/9 (F – 32), С – температура (в градусах) по шкале Цельсия, F – температура по шкале Фаренгейта.
Интервальная шкала – шкала количественная, для упорядочения данных (объектов) согласно отношениям эквивалентности, порядка и аддитивности. В ней определена метрика (начало отсчета, единица измерения и понятие расстояния между данными, объектами), поэтому решаема задача сравнения результатов тестирования.
У качественных шкал низкая точность измерения, у количественных – выше объективность.
Структура типов и уровней измерения приведена на рис. 6.1 .
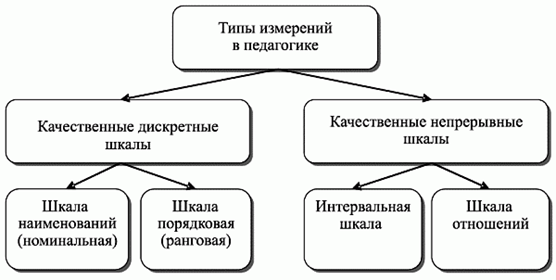
Рис. 6.1. Структура типов и уровней измерения, шкал. Источник: Звонников В.И., Челышкова М.Б. Современные средства оценивания результатов обучения: учеб. пособие для студ. вузов, 3-е изд., стер. - М.: Академия, 2009. - 224 с.
Часто используемая в тестологии шкала логитов переводится обычно в шкалу тестовых баллов.
Пример. Если участник ЕГЭ не выполнил ни одного задания и получил 0 первичных баллов, он получает ноль тестовых баллов, если же он выполнил все задания и получил максимально возможный первичный балл, он получает 100 тестовых баллов. Тестовые баллы остальных участников ЕГЭ вычисляются с помощью линейного преобразования, переводящего отрезок шкалы логитов, ограниченный оценкой в логитах, соответствующей одному первичному баллу и оценкой в логитах, соответствующей первичному баллу, на единицу меньшему максимально возможного в отрезок на шкале тестовых баллов от шести до девяноста четырех включительно. Например, формула перевода шкалы логитов в шкалу тестовых баллов может иметь вид:
![T=\{0,x<x_{\min};100,x>x_{\max},\left[\frac{6x_{\max}+88x-94x_{\min}}{x_{\max}-x_{\min}}+0.5\right],x_{min}<x<x_{\max}\},](/sites/default/files/tex_cache/1fa8debdb4ab0ca280fbbbb3ed4a9836.png)
где Т – тестовый балл, х – оценка уровня подготовленности участника ЕГЭ в логитах, xmin- оценка в логитах, соответствующая одному первичному баллу, xmax- оценка в логитах, соответствующая первичному баллу, на единицу меньшему, чем максимально возможный балл, [x] – целая часть х.
В нормативно-ориентированных тестах ставится задача определения рейтинга тестируемых в группе. Это место, естественно, зависит от "фона" - группы. Используют нормы, отражающие результаты тестирования для представительной выборки испытуемых.
Пример. Обычно для качественного такого теста около 70% результатов расположены в центре распределения ("под колоколом" кривой распределения) и имеют небольшую ошибку измерений, примерно по 5% (самых слабых и самых сильных результатов) в пологой части кривой распределения, они могут иметь очень большую ошибку измерения. Профессиональное тестирование, при обработке, эти концы или их части отбрасывает.
В критериально-ориентированных тестах ставится задача: сопоставить учебные достижения каждого испытуемого с запланированным для усвоения объемом знаний (умений, навыков). Это больше зависит уже от конкретно проверяемого содержания ГОС (программы).
Для устранения зависимости интерпретации результата тестированного от результатов в группе участников тестирования используются эмпирически, экспертно устанавливаемые нормы выполнения теста, с которыми сопоставляются первичные баллы конкретного испытуемого. Это процесс стандартизации теста, например, по среднему и стандартному отклонению индивидуальных баллов.
Часто используемые преобразования "сырых" баллов:
- процентильное, отражающее процент испытуемых из нормативной группы, результаты которых не выше данного значения первичного балла;
- Z-оценка, линейная оценка – отношение индивидуального отклонения тестовых баллов к стандартному отклонению по баллам всей группы испытуемых, а также линейные преобразования Z-оценки (Т-шкала и др.);
- шкалы станайнов и стенов (шкала Кэттела), получаемые делением шкалы первичных баллов на ряд интервалов.
Процентили устанавливают ранг показателя испытуемого в нормативной группе, показывая процент испытуемых в нормативной выборке, имеющих результаты не выше данных первичных баллов. Шкала процентилей нелинейна (нелинейно изменяется отклик на изменение в шкале первичных баллов на один балл), поэтому она может даже искажать реальную ситуацию.
Так называемая Z-шкала переводит индивидуальные результаты в стандартную шкалу, которая характерна двумя основными общими параметрами: средним баллом и дисперсией. Z-оценку i-го тестированного находят по формуле:
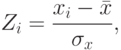
где xi первичные баллы испытуемого; 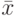 – среднее значение в группе;
– среднее значение в группе; 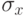 – стандартное отклонение.
– стандартное отклонение.
Эта шкала приводит баллы обучаемых по различным тестам к единому и удобному для сравнения виду.
Z-шкала неудобна для практического использования: баллы могут принимать вещественные значения (обычно от –3 до +3; отрицательность оценки указывает на то, что результат ниже среднегруппового); округлять их часто нельзя – теряется различающая способность, информативность.
Поэтому Z-оценки преобразуются с сохранением формы распределения по общей формуле:
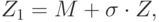
где Z1 – новая, преобразованная оценка, М – новое среднее,  - новое стандартное отклонение.
- новое стандартное отклонение.
Пример. T-шкала (параметры 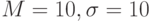 ) задается преобразованием:
) задается преобразованием: 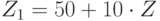 . Шкала СЕЕВ (
. Шкала СЕЕВ (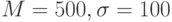 ):
): 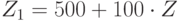 . Шкала IQ (
. Шкала IQ (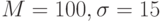 ):
): 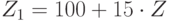 .
.
Шкалы результатов, например, от 1 до 10 – удобны и наглядны. Разбивая нормальное распределение на 9 интервалов, получаем шкалу станайнов со средней, равной 5, стандартным отклонением – около 2. В ней 4% наихудших результатов имеют станайн 1, наилучших – станайн 9, следующие (предшествующие) 7%, соответственно, станайны 2 и 8, далее 12% – станайны 3 и 7, 17% – станайны 4 и 6 и оставшиеся 20% средних результатов – станайн 5.
В шкале стенов, результаты делятся равномерно на 10 частей с интервальным расстоянием (между соседними единицами) – 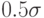 , средним принимаемым равным 5,5.
, средним принимаемым равным 5,5.

