Операции с разрядами (битами) в языке С
Теоретическая часть
16.1. Базовые системы счисления
В языке программирования С предусмотрена возможность по управлению отдельными разрядами (битами) значения переменной. Эта возможность связывается с различным представлением числа в компьютере, а именно с различными основаниями системы счисления: двоичной системой счисления, восьмеричной системой счисления, шестнадцатеричной системой счисления.
У бита возможны только два значения: 0 и 1. Техническая реализация таких состояний легко реализуется, например, включено–выключено, положительное значение напряжения–отрицательное значение напряжения (определенного уровня) и т.д.
В языке программирования С термин байт используется для обозначения размера (разрядности) хранения набора символов. Поэтому в языке С байт может содержать 8, 9, 16 и другое количество разрядов. Однако в характеристиках модулей памяти и систем передачи данных предполагается, что байт содержит восемь разрядов [16.1].
Разряды байта пронумерованы справа налево числами от 0 до 7. Седьмой разряд (крайний левый) называется старшим, а нулевой разряд (крайний правый) – младшим.
Байт имеет наибольшее значение, когда все его разряды установлены, т.е. имеют значение 1. Например, для 8 разрядов с учетом двоичной системы счисления в случае возможного наибольшего значения получим:
Наименьшему значению соответствует комбинация нулей 00000000, которая представляет собой просто нуль [9].
Байт может хранить числа от 0 до 255, что составляет 256 возможных значений. Программа может интерпретировать комбинацию разрядов иначе и применять байт для хранения чисел от –128 до 127, что составляет 256 возможных значений. Например, тип unsigned char обычно характеризуется использованием байта для представления чисел в диапазоне от 0 до 255, тип signed char – до 127.
В основании восьмеричной системы счисления лежит число 8 (23). Каждое знакоместо восьмеричного числа соответствует определенной степени восьми. Для записи используются цифры от 0 до 7. Каждая цифра восьмеричного числа соответствует трем двоичным цифрам. Двоичные эквиваленты восьмеричных цифр представлены в табл. 16.1.
| Двоичные эквиваленты восьмеричных цифр | |
|---|---|
| Восьмеричная цифра | Двоичный эквивалент |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
В шестнадцатеричной системе счисления используются степени числа 16 и цифры от 0 до 15. Для представления цифр, соответствующих десятичным значениям от 10 до 15, используются буквы от A до F [16.1]. Например, шестнадцатеричное число A3F (в языке С записывается как 0xA3F ) представляет значение
 (по основанию 10).
(по основанию 10).
В приведенной записи числу 10 соответствует А, а числу 15 – F.
Язык С допускает использование букв нижнего и верхнего регистра (строчные и прописные буквы) для обозначения шестнадцатеричных цифр. Таким образом, число 2 623 в шестнадцатеричной системе счисления можно записать как 0xA3F, так и 0xa3f.
Каждая цифра шестнадцатеричного числа соответствует 4-значному двоичному числу [16.1]. Поэтому две шестнадцатеричных цифры соответствуют одному восьмиразрядному байту. Первая цифра представляет 4 старших разряда, а вторая цифра – 4 младших разряда.
Соответствие между шестнадцатеричными цифрами, десятичными и двоичными числами показано в табл. 16.2.
| Эквиваленты шестнадцатеричных чисел | ||
|---|---|---|
| Десятичное число | Шестнадцатеричная цифра | Двоичный эквивалент |
| 1 | 2 | 3 |
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
В языке С существуют два средства управления разрядами [16.1]. Первое представляет собой набор поразрядных операций, а второе – форму полей данных, которое предоставляет доступ к разрядам значения типа int.
Далее будут использоваться 8-разрядные числа в двоичной системе счисления.
16.2. Логические поразрядные операции
В языке программирования С существуют два вида поразрядных операций: логические операции и операции сдвига [16.1].
Поразрядные операции выполняются над каждым разрядом независимо от разрядов слева или справа. Поразрядные операции выполняются над целыми числами. Рассмотрим логические поразрядные операции.
Унарная операция 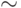 преобразовывает все единицы в нули и все нули в единицы (предполагается, что операции производятся над двоичными числами). Данную операцию называют также операцией "дополнение", т.е. когда все биты, равные 0, устанавливаются в 1, а когда все биты, равные 1, – устанавливаются в 0.
преобразовывает все единицы в нули и все нули в единицы (предполагается, что операции производятся над двоичными числами). Данную операцию называют также операцией "дополнение", т.е. когда все биты, равные 0, устанавливаются в 1, а когда все биты, равные 1, – устанавливаются в 0.
Поразрядная операция И обозначается символом &.
Двоичная операция & создает новое значение за счет выполнения поразрядного сравнения двух операндов. Для каждой позиции результирующий разряд будет иметь значение 1 только в случае, когда соответствующие разряды обоих операндов имеют значение 1. Можно сказать, что когда над двумя значениями производится операция поразрядного умножения &, то двоичные представления чисел сравниваются бит за битом [2]. Например, пусть одна переменная w1 есть число 25, а другая w2 – число 77. Соответственно в двоичном представлении 25 = 0000000000011001, 77 = 0000000001001101. Тогда в результате поразрядной операции & получим число w3 = w1 & w2. Результат действия оператора & можно представить следующим образом:
| Поразрядная операция И (&) |
| w1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 (25) |
| w2 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 (77) |
| w3 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 (9) |
В результате поразрядной операции "&" над двумя числами (25 и 77 в двоичном представлении), которые имеют, например, 16 бит, получили новое число, т.е. 9.
Поразрядный оператор "&" часто используется для операций маскирования. С его помощью принудительно можно установить заданный бит данных в значение 0. Например, в утверждении
w3 = w1 & 3;
переменной w3 присваивается значение переменной w1, для которой выполнена поразрядная операция & со значением 3. При этом все биты левее двух младших битов устанавливаются в 0, а остальные биты сохраняют свое значение [16.2]. Маска представляет собой некоторую комбинацию разрядов [16.1]. Разряды маски с нулевыми значениями можно считать аналогом непрозрачных ячеек реальной маски, а разряды со значениями 1 – прозрачными ячейками.
Поразрядная операция & называется также конъюнкцией, или логическим умножением. Применяется часто обозначение AND.
Поразрядная операция ИЛИ обозначается символом |.
Когда над двумя значениями производится операция поразрядно ИЛИ, то последовательно сравниваются значения всех битов при двоичном представлении этих значений [5]. Если при этом соответствующий бит имеет значение 1 в первом или втором операнде, то результирующее значение будет равно 1. Рассмотрим предыдущий пример с поразрядной операции ИЛИ:
| Поразрядная операция ИЛИ (|) |
| w1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 (25) |
| w2 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 (77) |
| w3 0 0 0 0 0 0 0 0 0 1 0 1 1 1 0 1 (93) |
Поразрядную операцию ИЛИ (|) обычно используют для установки заданных битов слова в 1. Логическую операцию ИЛИ называют также включающей дизъюнкцией, или логическим сложением. Часто применяется обозначение OR.
Поразрядная операция исключающего ИЛИ ( ^ ) работает следующим образом [5]. Сравниваются соответствующие биты двух операндов, и если только один из битов равен 1, то результат будет равен 1. А при равенстве обоих соответствующих битов или 0, или 1 результат будет равен 0. Для двух операндов b1, b2 при использовании исключающего ИЛИ ( ^ ) справедлива таблица истинности (табл. 16.3).
| Таблица истинности операции исключающего ИЛИ ( ^ ) | ||
| b1 | b2 | b1 ^ b2 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Если операцию исключающего ИЛИ ( ^ ) использовать для одного и того же значения, то в результате будет получено нулевое значение. Этот прием часто использовался программистами на языке ассемблера как наиболее быстрый путь установить значение в нуль или сравнить два значения на их равенство. Этот способ не рекомендуется использовать в языке программирования С, так как при этом скорость работы не повышается, а программа становится менее понятной [16.2].
Операция исключающего ИЛИ ( ^ ) может применяться для перестановки значений двух переменных без выделения дополнительной памяти (и, соответственно, без использования дополнительной переменной).
Поразрядная операция исключающего "ИЛИ" называется также исключающей дизъюнкцией. Часто применяется обозначение XOR.
1.3. Поразрядные операции сдвига
Оператор сдвига влево: <<
Когда оператор сдвига влево ( << ) выполняется над некоторым значением, все биты, составляющие это значение, сдвигаются влево [16.2]. Связанное с этим оператором число показывает количество бит, на которое значение должно переместиться. Биты, которые сдвигаются со старшего разряда, считаются потерянными, а на место младших битов всегда помещаются нули.
Оператор сдвига вправо: >>
Операция сдвига вправо ( >> ) сдвигает разряды левого операнда вправо на количество позиций, указываемое правым операндом. Выходящие за правую границу разряды теряются. Для типов данных без знака ( unsigned ) освобождаемые слева позиции заполняются нулями. Для знаковых типов данных результат зависит от используемой системы. Освобождаемые позиции могут заполняться нулями либо копиями знакового (первого слева) разряда [16.1].
Поразрядные операции сдвига могут служить удобным и эффективным (в зависимости) средством выполнения операций умножения и деления на числа, представляющие собой степени двойки [16.1]. Такие операции аналогичны смещению десятичной точки при умножении или делении на 10.
Второй метод управления разрядами состоит в использовании битового (разрядного) поля [9], которое представляет собой просто последовательную цепочку разрядов в рамках значения типа signed int или unsigned int.
Битовое поле может быть только элементом структуры или объединения и вне объектов этих типов не встречается [16.3].
Битовое поле создается путем объявления структуры (объединения), которая помечает каждое поле и определяет его разряд.
Приведем пример из [16.2] с использованием битовых полей в структуре:
struct packed_struct {
unsigned int : 3;
unsigned int f1 : 1;
unsigned int f2 : 1;
unsigned int f3 : 1;
unsigned int type : 8;
unsigned int index : 18;
};В созданном шаблоне-структуре с дескриптором (именем-этикеткой) packed_struct первый член не имеет имени. Символ , ":3" задает три безымянных бита. Второй, третий и четвертый члены структуры, f1, f2, f3, также имеют тип unsigned int. Символ ":1" говорит о том, что в данном члене структуры будет храниться 1 бит. Член структуры с именем type в памяти занимает 8 бит. Член структуры index рассчитан на хранение 18 бит.
Для заданного шаблона структуры можно определить структурную переменную, например:
struct packed_struct packed_data;
После этого можно присваивать значения полям структуры, например:
packed_data.type = 7;
Если ранее была объявлена какая-то переменная, например, n, то присвоение может быть таким:
packed_data.type = n;
При этом нет необходимости беспокоиться о том, что значение переменной n будет слишком большим. Только младшие 8 бит будут учитываться при присваивании значения для поля packed_data.type.
Для извлечения битовых полей структуры можно использовать обычное утверждение:
n = packed_data.type;
В приведенном примере после извлечения значения поля type будет произведен сдвиг в сторону младших бит.
Битовые поля могут быть объявлены только как тип int (в стандарте С99 также _Bool ). Если битовое поле имеет тип int, то этот знаковый ( signed ) или беззнаковый ( unsigned ) тип зависит от реализации.
Для исключения неоднозначности следует использовать явные объявления: signed int или unsigned int.
Битовые поля нельзя объединять в массивы. Нельзя использовать адрес битового поля, поэтому не может быть такого типа, как "указатель на битовое поле" [16.2]. Компилятор языка программирования С не переупорядочивает битовые поля для получения оптимального распределения памяти. Но в некоторых случаях может производиться выравнивание за счет безымянного поля. Это может использоваться для выравнивания следующего поля структуры по границе блока [16.2].
С помощью битовых полей можно формировать объекты с длиной внутреннего представления, не кратной байту.
