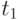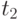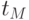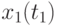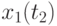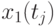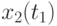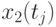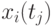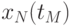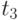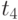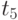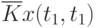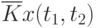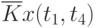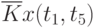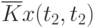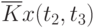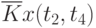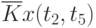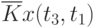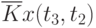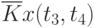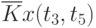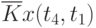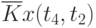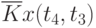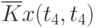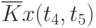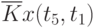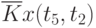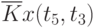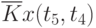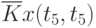|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Обработка результатов имитационного эксперимента
Современные системы имитационного моделирования предоставляют возможность выполнять автоматически стандартную обработку результатов моделирования:
- определение характеристик случайных параметров, главным образом, их матожиданий и дисперсий;
- фиксация минимальных и максимальных значений исследуемых величин;
- частотное распределение результатов измерений (построение гистограмм);
- расчет коэффициентов использования объектов модели и др.
Часто инженеру приходится выполнять более сложную обработку:
- определение функциональных или статистических зависимостей между исследуемыми величинами;
- выявление существенных или несущественных факторов, участвующих в эксперименте;
- сравнение случайных параметров процесса с целью определения значимости расхождения или совпадения их характеристик и др.
В наиболее развитых системах моделирования предусмотрены средства, обеспечивающие выполнение этих обработок. Но в любом случае инженер должен понимать сущность обработки, уметь правильно готовить исходные данные, грамотно интерпретировать результаты обработки. При наличии альтернатив обоснованно выбирать метод обработки и, при необходимости, разрабатывать соответствующие процедуры.
5.1. Характеристики случайных величин и процессов
В результате эксперимента с имитационной статистической моделью, состоящего из  наблюдений, мы получаем
наблюдений, мы получаем  значений исследуемой случайной величины
значений исследуемой случайной величины 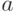 :
:
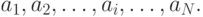
По этим данным нужно дать всестороннее описание величины a.
Определить случайную величину - это значит определить ее характеристики. В общем случае:
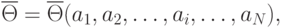
где  - оценка характеристики случайной величины. Под характеристикой понимают следующее.
- оценка характеристики случайной величины. Под характеристикой понимают следующее.
Во-первых, это характеристика величины:
- матожидание (среднее арифметическое);
- медиана (срединное значение);
- мода (наиболее вероятное значение);
- среднее геометрическое и др.
В рамках задач, характерных для нашей профессии, наиболее актуальным является матожидание. Как известно, матожидание определяет центр рассеивания случайной величины, наиболее полно отмечающее ее положение на числовой оси. Будем обозначать матожидание случайной величины 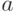 так:
так: ![M[a]](/sites/default/files/tex_cache/84f1c6a6971e2c862d7a52fbfb072a62.png) .
.
Во-вторых, это характеристики рассеивания:
- дисперсия (матожидание квадрата отклонения случайной величины a );
- среднее квадратическое отклонение (квадратный корень из дисперсии); иногда целесообразно пользоваться этой характеристикой, так как она имеет размерность самой случайной величины;
- размах (
 ).
).
В-третьих, это характеристика связи между случайными величинами (корреляция); степень связи определяется величиной коэффициента корреляции  . В случайном процессе связь между значениями случайной функции в моменты времени
. В случайном процессе связь между значениями случайной функции в моменты времени 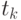 ,
,  определяет коэффициент автокорреляции
определяет коэффициент автокорреляции 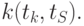
В-четвертых, это характеристика закона распределения вероятностей случайной величины в виде плотности или функции распределения: 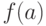 или
или 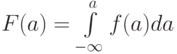 .
.
5.2. Требования к оценкам характеристик
Ограниченное число реализаций модели не позволяет точно определить значения этих характеристик, а только приближенно,
то есть так называемые оценки характеристик \Theta . Степень приближения оценок  зависит от методов их вычислений (формул). Поскольку
зависит от методов их вычислений (формул). Поскольку  , где
, где 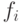 - случайные значения искомого параметра, то величина
- случайные значения искомого параметра, то величина  - случайная со своими значениями матожидания, дисперсии и т. п.
- случайная со своими значениями матожидания, дисперсии и т. п.
Как правило, математическая статистика может предложить разные формулы для вычисления оценки одной и той же характеристики. Следовательно, оценки могут быть более или менее точными или даже вовсе непригодными при имитационном моделировании.
Чтобы оценка наилучшим образом представляла искомую характеристику, нужно, чтобы она обладала следующими свойствами:
- несмещенностью;
- состоятельностью;
- эффективностью.
Несмещенность. Это свойство означает, что оценка не содержит систематической ошибки. Т. е., математическое ожидание оценки совпадает с действительным значением характеристики  :
:
![M[\overline{\Theta}] = M[\Theta].](/sites/default/files/tex_cache/c23f9fb7ef2095f27405aecc3b5fca0d.png)
Состоятельность. Это свойство означает, что оценка  приближается сколь угодно близко к истинному значению характеристики
приближается сколь угодно близко к истинному значению характеристики ![\Theta(M[\Theta])](/sites/default/files/tex_cache/85c5f26bb88d936d65ad4e360c83ae2e.png) по мере увеличения объема выборки, т. е. увеличения числа реализаций модели. Формально это свойство записывают так:
по мере увеличения объема выборки, т. е. увеличения числа реализаций модели. Формально это свойство записывают так:
![P( |\overline{\Theta}-M[\Theta]| < \varepsilon)\to 1](/sites/default/files/tex_cache/772484694feab22943fb89869e34e23b.png)
при 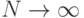 и любом
и любом 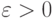 .
.
Именно это свойство являлось определяющим при нахождении количественной связи между точностью, достоверностью оценок и числом реализаций модели.
Эффективность. Это свойство означает, что из всех несмещенных и состоятельных оценок следует предпочесть ту, у которой разброс значений меньше. Иначе: эффективной оценкой характеристики случайной величины называют ту, которая имеет наименьшую дисперсию:
![D[\overline{\Theta}]= \min{\overline{\Theta}_k},](/sites/default/files/tex_cache/34e9b43a5633f97faa0efd5de8a0e2e2.png)
 - число возможных оценок.
- число возможных оценок.
В исследовании свойств оценок большая заслуга принадлежит англичанину Рональду А. Фишеру. Основные результаты он получил в 1912 г., когда ему было 22 года.
5.3. Оценка характеристик случайных величин и процессов
Наиболее используемые оценки характеристик приведены в табл. 5.1.
| Характеристика | Оценка | Среднее квадратическое отклонение оценки |
|---|---|---|
Матожидание ![M[x]=\int\limits_{-\infty}^{-\infty}{xf(x)dx}](/sites/default/files/tex_cache/9a7be4961c25f179e715415da87ce004.png)
|
 |
 |
Дисперсия ![D[x]=M[x^{2}]-(M[x])^{2}](/sites/default/files/tex_cache/f193473ea338354309736f842637f1b7.png)
|
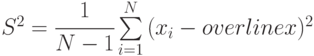 |
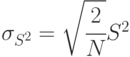 |
Среднее квадратическое отклонение ![\sigma_{x} = \sqrt{D[x]}](/sites/default/files/tex_cache/c482db42d316c68375733ad369b24606.png)
|
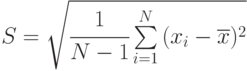 |
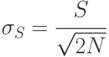 |
Вероятность события 
|
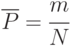 |
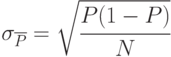 |
Коэффициент корреляции 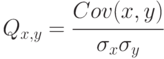
|
 |
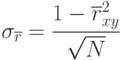 |
Все оценки несмещенные, состоятельные, эффективные.
Проблемами оценок занимался и Абрагам Вайльд, американский математик австрийского происхождения.
Приведем для иллюстрации два примера.
Пример 5.1. Оценка матожидания случайной величины 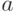 - среднее арифметическое
- среднее арифметическое
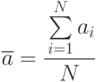
является несмещенной, состоятельной и эффективной.
Оценка в виде медианы не является эффективной, так как дисперсия в этом случае
![D[\overline{a}_m]=\cfrac{\pi\sigma_a^2}{2N}](/sites/default/files/tex_cache/1c87b48b5dd1c904b084c54bee863946.png)
в  раз больше дисперсии
раз больше дисперсии ![D[\overline{a}]](/sites/default/files/tex_cache/cc44e7af5084a47419388866fe6e65dd.png) , равной, как известно,
, равной, как известно, ![D[\overline{a}]=\cfrac{\sigma_a^2}{N}](/sites/default/files/tex_cache/ac49885de8504e632578b2523f8104c0.png)
Пример 5.2. Выборочная дисперсия случайной величины 
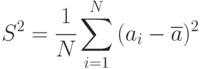
состоятельна, эффективна, но смещена. Смещение образовалось из-за того, что вместо неизвестного ![M[a]](/sites/default/files/tex_cache/84f1c6a6971e2c862d7a52fbfb072a62.png) в формуле стоит оценка
в формуле стоит оценка 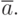
Несмещенная оценка имеет вид:
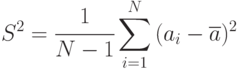
Иногда формулы для вычисления оценок матожидания и дисперсии используют в рекуррентной форме:
![M[\overline{a}]_i= M[\overline{a}]_{i-1}\cfrac{i-1}{i}+\cfrac{a_i}{i},\\
S_i^2 = S_{i-1}^2\cfrac{i-1}{i}+\cfrac{\left ( a_i - M[\overline{a}]_i \right )^2}{i},](/sites/default/files/tex_cache/3cd13f68c6b4f32fcc3d16181816c91b.png)
где ![M [\overline{a}]_i, M[\overline{a}]_{i-1},S^{2}_i, S^{2}_{i-1}](/sites/default/files/tex_cache/d04bb9632338d5c2c8116a5bcfdc2ce2.png) - оценки матожидания и дисперсии, вычисленные по данным
- оценки матожидания и дисперсии, вычисленные по данным  и (
и ( 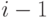 ) реализаций имитационной модели.
) реализаций имитационной модели.
Приведенные в табл. 5.1 ,формулы соответствуют нормальному закону распределения вероятностей исследуемой величины.
При исследовании случайного процесса 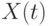 весь временной интервал
весь временной интервал 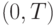 представляется последовательностью из
представляется последовательностью из 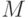 временных точек
временных точек 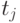 ,
, 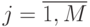 , в каждой из которых измеряется значение сечения
, в каждой из которых измеряется значение сечения 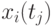 . Индекс
. Индекс  - номер реализации случайного процесса,
- номер реализации случайного процесса, 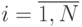 .
.
Полученные данные образуют матрицу сечений размером  , что и является моделью исследуемого процесса (табл. 5.2).
, что и является моделью исследуемого процесса (табл. 5.2).
Совокупность сечений в каждой временной точке 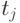 (столбец матрицы), представляет собой случайные числа некоторой случайной величины в общем случае со своими законами распределения, матожиданиями, дисперсиями:
(столбец матрицы), представляет собой случайные числа некоторой случайной величины в общем случае со своими законами распределения, матожиданиями, дисперсиями:
![\overline{x}(t_j)=\cfrac{1}{N}\sum\limits_{i=1}^{N}{x_i(t_j)},\,\,
S^2_{x(t_j)}= \cfrac{1}{N}\sum\limits_{i=1}^{N}{[x_i(t_j) - \overline{x}(t_j)]^2}](/sites/default/files/tex_cache/48018dbe48ac7d46df1165eec0ec2b15.png)
При решении практических задач последовательности этих оценок матожиданий и дисперсий, определенных в точках 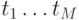 , достаточно полно представляют моделируемый случайный процесс. Оценки матожиданий
, достаточно полно представляют моделируемый случайный процесс. Оценки матожиданий 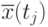 и дисперсий
и дисперсий 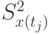 можно аппроксимировать подходящими кривыми в предположении непрерывности процесса.
можно аппроксимировать подходящими кривыми в предположении непрерывности процесса.
Иногда исследователя интересует связь сечений случайного процесса между собой. Степень зависимости между сечениями определяет автокорреляционная функция. Оценка ее имеет вид:
![\overline{K}x(t_k,t_s) = \cfrac{1}{N}\sum\limits_{i=1}^{N}{[x_i(t_k) - \overline{x}(t_k)]\cdot [x_i(t_s) - \overline{x}(t_s)]}](/sites/default/files/tex_cache/1e954b52d331c59046ef6ab297f00422.png) |
( t_s)]) |
где 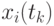 и
и 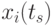 - значения сечений в точках
- значения сечений в точках 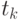 и
и 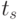 соответственно
соответственно 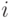 -й реализации;
-й реализации;
 и
и 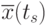 - оценки матожиданий совокупности сечений в точках
- оценки матожиданий совокупности сечений в точках 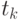 и
и 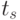 соответственно.
соответственно.
Данные расчета значений автокорреляционной функции 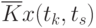 ,
, 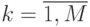 ,
,  помещают в таблицу, которая и является табличным определением ее. В случае необходимости данные таблицы могут быть представлены подходящей аппроксимирующей кривой.
помещают в таблицу, которая и является табличным определением ее. В случае необходимости данные таблицы могут быть представлены подходящей аппроксимирующей кривой.
Пример таблицы значений 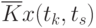 для случайного процесса,
для случайного процесса,
определенного пятью сечениями  , показан в табл. 5.3.
, показан в табл. 5.3.
Очевидно, что рассчитывать все значения 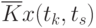 для заполнения таблицы (в данном примере их 25) не надо, так как значения
для заполнения таблицы (в данном примере их 25) не надо, так как значения  при
при  ("северо-западная диагональ") представляют собой значения соответствующих дисперсий. И
("северо-западная диагональ") представляют собой значения соответствующих дисперсий. И  , что исключает необходимость расчета половины оставшихся значений коэффициентов автокорреляционной функции, расположенных выше или ниже упомянутой диагонали.
, что исключает необходимость расчета половины оставшихся значений коэффициентов автокорреляционной функции, расположенных выше или ниже упомянутой диагонали.