|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Оптимальные каркасы
Задача об оптимальном каркасе
Задача об оптимальном каркасе (стягивающем дереве) состоит в следующем.
Дан обыкновенный граф  и весовая функция на множестве
ребер
и весовая функция на множестве
ребер 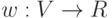 . Вес множества
. Вес множества 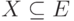 определяется как сумма
весов составляющих его ребер. Требуется в графе
определяется как сумма
весов составляющих его ребер. Требуется в графе  найти каркас
минимального веса. В этом разделе будем предполагать, что граф
найти каркас
минимального веса. В этом разделе будем предполагать, что граф  связен, так что решением задачи всегда будет дерево. Для решения
задачи об оптимальном каркасе известно несколько алгоритмов. Рассмотрим
два из них.
связен, так что решением задачи всегда будет дерево. Для решения
задачи об оптимальном каркасе известно несколько алгоритмов. Рассмотрим
два из них.
Алгоритм Прима
В алгоритме Прима на каждом шаге рассматривается частичное решение задачи,
представляющее собой дерево. Вначале это дерево состоит из единственной
вершины, в качестве которой может быть выбрана любая вершина графа. Затем
к дереву последовательно добавляются ребра и вершины, пока не получится
остовное дерево, т.е. каркас. Для того чтобы из текущего дерева при
добавлении нового ребра опять получилось дерево, это новое ребро должно
соединять вершину дерева с вершиной, еще не принадлежащей дереву. Такие
ребра будем называть подходящими относительно рассматриваемого
дерева. В алгоритме Прима применяется следующее правило выбора: на каждом
шаге из всех подходящих ребер выбирается ребро наименьшего веса. Это ребро
вместе с одной новой вершиной добавляется к дереву. Если обозначить
через  и
и  множества вершин и ребер строящегося
дерева, то алгоритм Прима можно представить следующим образом.
множества вершин и ребер строящегося
дерева, то алгоритм Прима можно представить следующим образом.
Алгоритм 1. Построение оптимального каркаса методом Прима
-
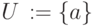 , где
, где  - произвольная
вершина графа
- произвольная
вершина графа 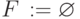
-
while
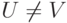 do
do
- найти ребро наименьшего веса
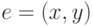 среди всех подходящих ребер
среди всех подходящих ребер 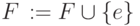
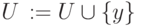
Докажем, что алгоритм Прима действительно находит оптимальный каркас.
Дерево  назовем фрагментом, если существует такой
оптимальный каркас
назовем фрагментом, если существует такой
оптимальный каркас  графа
графа  , что
, что  является
подграфом дерева
является
подграфом дерева  . Иначе говоря, фрагмент - это
дерево, которое
можно достроить до оптимального каркаса.
. Иначе говоря, фрагмент - это
дерево, которое
можно достроить до оптимального каркаса.
Теорема 1. Если  - фрагмент,
- фрагмент,  - подходящее ребро наименьшего веса относительно
- подходящее ребро наименьшего веса относительно  , то
, то  - фрагмент.
- фрагмент.
Доказательство. Пусть  - оптимальный каркас, содержащий
- оптимальный каркас, содержащий  в качестве подграфа. Если ребро
в качестве подграфа. Если ребро  принадлежит
принадлежит  ,
то
,
то  - подграф
- подграф  и,
следовательно, фрагмент.
Допустим,
и,
следовательно, фрагмент.
Допустим,  не принадлежит
не принадлежит  .
Если добавить ребро
.
Если добавить ребро  к дереву
к дереву  , то
образуется цикл.
В этом цикле есть еще хотя бы одно подходящее ребро относительно
, то
образуется цикл.
В этом цикле есть еще хотя бы одно подходящее ребро относительно  (никакой цикл, очевидно, не может содержать единственное подходящее
ребро). Пусть
(никакой цикл, очевидно, не может содержать единственное подходящее
ребро). Пусть  - такое ребро. Тогда подграф
- такое ребро. Тогда подграф 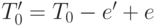 ,
получающийся из
,
получающийся из  удалением ребра
удалением ребра  и добавлением ребра
и добавлением ребра  , тоже будет деревом.
Так как
, тоже будет деревом.
Так как 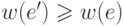 , то
, то 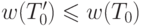 .
Но
.
Но  - оптимальный
каркас, следовательно,
- оптимальный
каркас, следовательно,  и
и 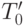 - тоже
оптимальный каркас. Но
- тоже
оптимальный каркас. Но  является подграфом графа
является подграфом графа 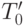 и, следовательно, фрагментом.
и, следовательно, фрагментом.
Дерево, состоящее из единственной вершины, очевидно, является фрагментом.
Из теоремы 1 следует, что если после некоторого количества шагов алгоритма
Прима дерево  является фрагментом, то оно будет фрагментом и
после следующего шага. Следовательно, и окончательное решение, полученное
алгоритмом, будет фрагментом, т.е. оптимальным каркасом.
является фрагментом, то оно будет фрагментом и
после следующего шага. Следовательно, и окончательное решение, полученное
алгоритмом, будет фрагментом, т.е. оптимальным каркасом.
