Трансфинитная индукция
Термины " индукция" и " рекурсия" часто употребляются
вперемежку. Например, определение факториала  как функции
как функции 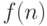 ,
для
которой
,
для
которой 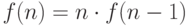 при
при  и
и  ,
называют и " индуктивным", и " рекурсивным". Мы будем
стараться разграничивать эти слова так: если речь идет о
доказательстве чего-то сначала для
,
называют и " индуктивным", и " рекурсивным". Мы будем
стараться разграничивать эти слова так: если речь идет о
доказательстве чего-то сначала для 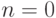 , затем для
, затем для 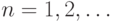 , причем каждое утверждение опирается на
предыдущее, то это индукция. Если же мы определяем
что-то
сначала для
, причем каждое утверждение опирается на
предыдущее, то это индукция. Если же мы определяем
что-то
сначала для 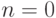 , потом для
, потом для 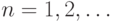 , причем
определение каждого нового значения использует ранее
определенные, то это рекурсия.
, причем
определение каждого нового значения использует ранее
определенные, то это рекурсия.
Наша цель - научиться проводить индуктивные доказательства и давать рекурсивные определения не только для натуральных чисел, но и для других вполне упорядоченных множеств.
Доказательства по индукции мы уже обсуждали, говоря о фундированных множествах (см. "лекцию 8" ), и сейчас ограничимся только одним примером.
Теорема 17.
Пусть  - вполне упорядоченное множество, а
- вполне упорядоченное множество, а 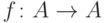 -
возрастающее отображение (то есть
-
возрастающее отображение (то есть  при
при  ).
Тогда
).
Тогда 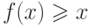 для всех
для всех 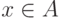 .
.
Доказательство.
Согласно принципу индукции (теорема 15)
достаточно доказать неравенство 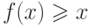 , предполагая, что
, предполагая, что 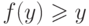 при всех
при всех 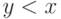 . Пусть это не так
и
. Пусть это не так
и  . Тогда
по монотонности
. Тогда
по монотонности 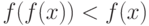 . Но, с другой стороны,
элемент
. Но, с другой стороны,
элемент 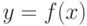 меньше
меньше  , и потому по предположению индукции
, и потому по предположению индукции 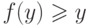 , то
есть
, то
есть 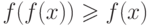 .
.
Если угодно, можно в явном виде воспользоваться существованием
наименьшего элемента и изложить это же рассуждение так. Пусть
утверждение теоремы неверно. Возьмем наименьшее  , для
которого
, для
которого  . Но тогда
. Но тогда 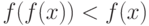 по
монотонности и
потому
по
монотонности и
потому  не является наименьшим вопреки предположению.
не является наименьшим вопреки предположению.
Наконец, это рассуждение можно пересказать и так:
если 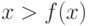 ,то по монотонности
,то по монотонности
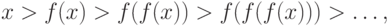
Теперь перейдем к рекурсии. В определении факториала 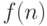 выражалось
через
выражалось
через 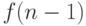 . В общей ситуации значение
. В общей ситуации значение 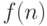 может использовать не только одно предыдущее значение функции,
но и все значения на меньших аргументах. Например, можно
определить функцию
может использовать не только одно предыдущее значение функции,
но и все значения на меньших аргументах. Например, можно
определить функцию  , сказав, что
, сказав, что 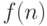 на единицу больше суммы всех предыдущих значений, то
есть
на единицу больше суммы всех предыдущих значений, то
есть 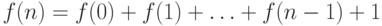 ; это вполне
законное
рекурсивное определение (надо только пояснить, что пустая
сумма считается равной нулю, так что
; это вполне
законное
рекурсивное определение (надо только пояснить, что пустая
сумма считается равной нулю, так что  ).
).
112. Какую функцию  задает такое определение?
задает такое определение?
Как обобщить эту схему на произвольные вполне упорядоченные
множества вместо натурального ряда? Пусть  вполне
упорядочено. Мы хотим дать рекурсивное определение некоторой
функции
вполне
упорядочено. Мы хотим дать рекурсивное определение некоторой
функции 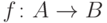 (где
(где  - некоторое
множество). Такое
определение должно связывать значение
- некоторое
множество). Такое
определение должно связывать значение  на некотором
элементе
на некотором
элементе 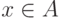 со значениями
со значениями 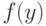 при
всех
при
всех 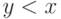 .
Другими словами, рекурсивное определение задает
.
Другими словами, рекурсивное определение задает  , предполагая
известным ограничение функции
, предполагая
известным ограничение функции  на начальный
отрезок
на начальный
отрезок 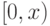 . Вот точная формулировка:
. Вот точная формулировка:
Теорема 18.
Пусть  - вполне упорядоченное множество. Пусть
- вполне упорядоченное множество. Пусть  -
произвольное множество. Пусть имеется некоторое рекурсивное
правило, то есть отображение
-
произвольное множество. Пусть имеется некоторое рекурсивное
правило, то есть отображение  , которое ставит в соответствие
элементу
, которое ставит в соответствие
элементу 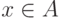 и функции
и функции 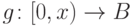 некоторый элемент
множества
некоторый элемент
множества  . Тогда существует и единственна функция
. Тогда существует и единственна функция 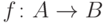 ,
для которой
,
для которой

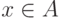 . (Здесь
. (Здесь  обозначает
ограничение
функции
обозначает
ограничение
функции  на начальный отрезок
на начальный отрезок 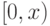 - мы
отбрасываем все
значения функции на элементах, больших или равных
- мы
отбрасываем все
значения функции на элементах, больших или равных  .)
.)Доказательство.
Неформально можно рассуждать так: значение  на минимальном
элементе определено однозначно, так как предыдущих значений
нет (сужение
на минимальном
элементе определено однозначно, так как предыдущих значений
нет (сужение  пусто). Тогда и на следующем
элементе значение функции
пусто). Тогда и на следующем
элементе значение функции  определено однозначно, поскольку на
предыдущих
(точнее, единственном предыдущем) функция
определено однозначно, поскольку на
предыдущих
(точнее, единственном предыдущем) функция  уже задана, и т.д.
уже задана, и т.д.
Конечно, это надо аккуратно выразить формально. Вот как это
делается. Докажем по индукции такое утверждение о произвольном
элементе 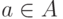 :
:
существует и единственно отображение
отрезка
в множество
, для которого рекурсивное определение (равенство, приведенное в условии) выполнено при всех
.
Будем называть отображение ![f\colon [0,a]\hm\to B](/sites/default/files/tex_cache/fb0df56c9eb1f539ea197b5a0f6bf46d.png) , обладающее
указанным свойством, корректным. Таким образом,
мы хотим доказать, что для каждого
, обладающее
указанным свойством, корректным. Таким образом,
мы хотим доказать, что для каждого 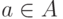 есть единственное
корректное отображение отрезка
есть единственное
корректное отображение отрезка ![[0,a]](/sites/default/files/tex_cache/13596d6674a86fdafa24c4c414033e58.png) в
в  .
.
Поскольку мы рассуждаем по индукции, можно предполагать, что для
всех 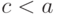 это утверждение выполнено, то есть существует и
единственно корректное отображение
это утверждение выполнено, то есть существует и
единственно корректное отображение ![f_c\colon [0,c]\hm\to B](/sites/default/files/tex_cache/414f02e7af54a34796db2926a8592e6b.png) .
(Корректность
.
(Корректность 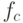 означает, что при всех
означает, что при всех 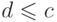 значение
значение 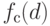 совпадает с предписанным по рекурсивному правилу.)
совпадает с предписанным по рекурсивному правилу.)
Рассмотрим отображения 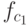 и
и 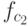 для двух
различных
для двух
различных 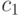 и
и 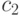 . Пусть, например,
. Пусть, например, 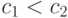 .
Отображение
.
Отображение 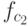 определено на большем отрезке
определено на большем отрезке ![[0,c_2]](/sites/default/files/tex_cache/9bad5c7ac85a1d6c133d544a42508155.png) . Если
ограничить
. Если
ограничить 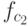 на
меньший отрезок
на
меньший отрезок ![[0,c_1]](/sites/default/files/tex_cache/9f6d70523bfbbe6637af1e538eafa8f5.png) , то оно совпадет с
, то оно совпадет с 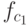 ,
поскольку ограничение корректного отображения на меньший
отрезок корректно (это очевидно), а мы предполагали
единственность на отрезке
,
поскольку ограничение корректного отображения на меньший
отрезок корректно (это очевидно), а мы предполагали
единственность на отрезке ![[0,c_1]](/sites/default/files/tex_cache/9f6d70523bfbbe6637af1e538eafa8f5.png) .
.
Таким образом, все отображения 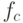 согласованы друг с другом,
то есть принимают одинаковое значение, если определены
одновременно. Объединив их, мы получаем некоторое единое
отображение
согласованы друг с другом,
то есть принимают одинаковое значение, если определены
одновременно. Объединив их, мы получаем некоторое единое
отображение  , определенное на
, определенное на 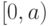 . Применив
к
. Применив
к  и
и  рекурсивное правило, получим некоторое значение
рекурсивное правило, получим некоторое значение 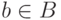 .
Доопределим
.
Доопределим  в точке
в точке  ,
положив
,
положив  .
Получится отображение
.
Получится отображение ![h\colon [0,a]\hm\to B](/sites/default/files/tex_cache/d6f4cc4cd80263c2fb655c7f746e2124.png) ; легко
понять, что оно корректно.
; легко
понять, что оно корректно.
Чтобы завершить индуктивный переход, надо проверить, что на
отрезке ![[0,a]](/sites/default/files/tex_cache/13596d6674a86fdafa24c4c414033e58.png) корректное отображение единственно. В самом деле, его
ограничения на отрезки
корректное отображение единственно. В самом деле, его
ограничения на отрезки ![[0,c]](/sites/default/files/tex_cache/0b77a0c57e4d83ea934d4ef032e10c08.png) при
при 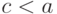 должны
совпадать с
должны
совпадать с 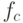 ,
поэтому осталось проверить однозначность в точке
,
поэтому осталось проверить однозначность в точке  -
что гарантируется рекурсивным определением (выражающим значение
в точке
-
что гарантируется рекурсивным определением (выражающим значение
в точке  через предыдущие).
На этом индуктивное доказательство заканчивается.
через предыдущие).
На этом индуктивное доказательство заканчивается.
Осталось лишь заметить, что для разных  корректные
отображения отрезков
корректные
отображения отрезков ![[0,a]](/sites/default/files/tex_cache/13596d6674a86fdafa24c4c414033e58.png) согласованы друг с другом (сужение
корректного отображения на меньший отрезок корректно,
применяем единственность) и потому вместе задают некоторую
функцию
согласованы друг с другом (сужение
корректного отображения на меньший отрезок корректно,
применяем единственность) и потому вместе задают некоторую
функцию 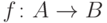 , удовлетворяющую рекурсивному
определению.
, удовлетворяющую рекурсивному
определению.
Существование доказано; единственность тоже понятна, так
как ограничение этой функции на любой отрезок ![[0,a]](/sites/default/files/tex_cache/13596d6674a86fdafa24c4c414033e58.png) корректно и потому однозначно определено, как мы видели.
корректно и потому однозначно определено, как мы видели.
Прежде чем применить эту теорему и доказать, что из двух
вполне упорядоченных множеств одно является отрезком другого,
нам потребуется ее немного усовершенствовать.
Нам надо предусмотреть ситуацию, когда рекурсивное правило
не всюду определено. Пусть, например, мы определяем последовательность
действительных чисел соотношением 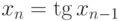 и начальным
условием
и начальным
условием 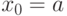 . При некоторых значениях
. При некоторых значениях  может
оказаться, что построение
последовательности обрывается, поскольку тангенс не определен
для соответствующего аргумента.
может
оказаться, что построение
последовательности обрывается, поскольку тангенс не определен
для соответствующего аргумента.
113. Докажите, что множество всех таких " исключительных"  (когда последовательность конечна) счетно.
(когда последовательность конечна) счетно.
Аналогичная ситуация возможна и для общего случая.
