Алгоритмы асимметричного шифрования
Криптоанализ алгоритмов с открытым ключом
Как и в случае симметричного шифрования, алгоритм шифрования с открытым ключом уязвим для лобовой атаки. Контрмера стандартная: использовать ключи большей длины.
Криптосистема с открытым ключом использует не инвертируемые математические функции. Сложность вычислений таких функций не является линейной от количества битов ключа, а возрастает быстрее, чем ключ. Таким образом, размер ключа должен быть достаточно большим, чтобы сделать лобовую атаку непрактичной, и достаточно маленьким для возможности практического шифрования. На практике размер ключа делают таким, чтобы лобовая атака была непрактичной, но в результате скорость шифрования оказывается достаточно медленной для использования алгоритма в общих целях. Поэтому шифрование с открытым ключом в настоящее время в основном ограничивается приложениями управления ключом и создания подписи, в которых требуется шифрование или подписывание небольшого блока данных.
Другая форма атаки состоит в том, чтобы найти способ вычисления закрытого ключа, зная открытый ключ. Невозможно математически доказать, что данная форма атаки исключена для конкретного алгоритма открытого ключа. Таким образом, любой алгоритм, включая широко используемый алгоритм RSA, является подозрительным.
Наконец, существует форма атаки, специфичная для способов использования систем с открытым ключом. Это атака вероятного сообщения. Предположим, например, что посылаемое сообщение состоит исключи-тельно из 56-битного ключа сессии для алгоритма симметричного шифро-вания. Противник может зашифровать все возможные ключи, используя открытый ключ получателя. В этом случае атака сводится к лобовой атаке на 56-битный симметричный ключ. Защита от подобной атаки состоит в добавлении определенного количества случайных битов в простые сообщения.
Основные способы использования алгоритмов с открытым ключом
Основными способами использования алгоритмов с открытым ключом являются шифрование / расшифрование, создание и проверка подписи и обмен ключа.
Шифрование с открытым ключом состоит из следующих шагов:
- Пользователь В создает пару ключей KUb и KRb, которые могут использоваться для шифрования и расшифрования передаваемых сообщений.
- Пользователь В передает пользователю A некоторым надежным способом свой ключ шифрования, т.е. открытый ключ KUb. Составляющий пару закрытый ключ KRb держится в секрете.
- Если А хочет послать конфиденциальное сообщение В, он шифрует сообщение, используя открытый ключ В KUb.
- Когда В получает сообщение, он расшифровывает его, используя свой закрытый ключKRb. Никто другой не сможет расшифровать сообщение, так как этот закрытый ключ знает только В.
- Если пользователь В надежно хранит свой закрытый ключ, никто не сможет расшифровать передаваемые сообщения.
Создание и проверка подписи состоит из следующих шагов:
- Пользователь A создает пару ключей KRA и KUA, которые могут использоваться для создания и проверки подписи.
- Пользователь A передает пользователю В некоторым надежным способом свой ключ проверки подписи, т.е. открытый ключ KUA. Составляющий пару закрытый ключ KRA держится в секрете.
- Если A хочет послать подписанное сообщение пользователю В, он создает подпись SignKRa[M] этого сообщения, используя свой закрытый ключ KRA.
- Когда В получает подписанное сообщение, он проверяет подпись VerKUa[M], используя открытый ключ KUA пользователя A. Никто другой не может подписать сообщение, так как этот закрытый ключ знает только A.
- До тех пор, пока пользователь A надежно хранит свой закрытый ключ, его подписи достоверны. Кроме того, невозможно изменить сообщение, не имея доступа к закрытому ключу А; тем самым обеспечивается аутентификация отправителя и целостность передаваемых данных. Все алгоритмы создания и проверки подписи имеют большую вычислительную нагрузку, так как связаны с возведением в большие степени. Более эффективным способом является подписывание небольшого блока битов, который является функцией от сообщения. Такой блок, называемый аутентификатором, должен обладать таким свойством, что любое изменение сообщения с большой веро-ятностью приводит к изменению его аутентификатора. Этот аутентификатор подписывается закрытым ключом отправителя, т.е. создается цифровая подпись. Далее эта технология будет рассматриваться в деталях.
Важно подчеркнуть, что описанный процесс создания подписи не обеспечивает конфиденциальность. Это означает, что сообщение, посланное таким способом, невозможно изменить, но можно подсмотреть. Это очевидно в том случае, если подпись основана на аутентификаторе, так как само сообщение передается в явном виде. Но даже если осуществляется подписывание всего сообщения, конфиденциальность не обеспечивается, так как любой может получить исходное сообщение, используя открытый ключ отправителя.
Аутентификация защищает двух участников, которые обмениваются сообщениями, от взаимодействия с некоторой третьей стороной. Однако аутентификация, выполняемая с использованием общего секрета (пароля), не защищает участников друг от друга, тогда как и между ними тоже могут возникать определенные формы споров.
Например, предположим, что A посылает B аутентифицированное сообщение, и аутентификация осуществляется на основе общего секрета. Рассмотрим возможные проблемы, которые могут при этом возникнуть:
B может подделать сообщение и утверждать, что оно пришло от А. B достаточно просто создать сообщение и присоединить аутентификационный код, используя ключ, который разделяют A и B.
A может отрицать, что он посылал сообщение B. Так как B может подделать сообщение, у него нет способа доказать, что A действительно посылал его.
В ситуации, когда обе стороны не доверяют друг другу, необходимо нечто большее, чем аутентификация на основе общего секрета. Возможным решением подобной проблемы является использование цифровой подписи. Цифровая подпись должна обладать следующими свойствами:
1. Должна быть возможность проверить автора, дату и время создания подписи.
2. Должна быть возможность аутентифицировать содержимое во время создания подписи.
3. Подпись должна быть проверяема третьей стороной для разрешения споров.
Таким образом, создание цифровой подписи включает сервис аутентификации отправителя.
На основании этих свойств можно сформулировать следующие требования к цифровой подписи:
- Подпись должна быть битовым образцом, который зависит от подписываемого сообщения.
- Подпись должна использовать некоторую уникальную информацию отправителя для предотвращения подделки или отказа.
- Создавать цифровую подпись должно быть относительно легко.
- Должно быть относительно легко проверять цифровую подпись.
- Должно быть вычислительно невозможно подделать цифровую подпись как созданием нового сообщения для существующей цифровой подписи, так и созданием ложной цифровой подписи для данного сообщения.
- Цифровая подпись должна быть достаточно компактной и не занимать много памяти.
Сильная хэш-функция, зашифрованная закрытым ключом отправителя, удовлетворяет перечисленным требованиям.
Обмен ключей: две стороны взаимодействуют для обмена ключом сессии, который в дальнейшем можно использовать в алгоритме симметричного шифрования.
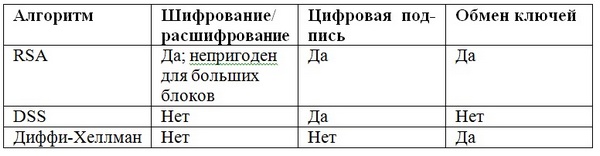
Некоторые алгоритмы можно задействовать тремя способами, в то время как другие могут использоваться одним или двумя способами.
Перечислим наиболее популярные алгоритмы с открытым ключом и возможные способы их применения.
Таблица 4.1