Хэш-функции
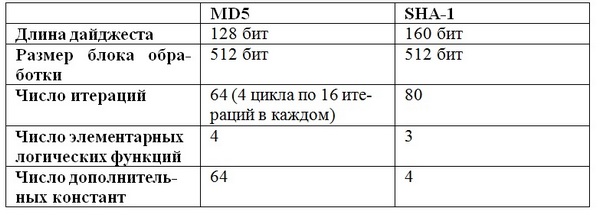
Сравнение SHA-1 и MD5
Оба алгоритма, SHA-1 и MD5, произошли от MD4, поэтому имеют много общего.
Можно суммировать ключевые различия между алгоритмами.
Таблица 3.2
Сравним алгоритмы MD5 и SHA-1.
- Безопасность: наиболее очевидное и наиболее важное различие состоит в том, что дайджест SHA-1 на 32 бита длиннее, чем дайджест MD5. Если предположить, что оба алгоритма не содержат каких-либо структурированных данных, которые уязвимы для аналитиче-ских атак, то SHA-1 является более стойким алгоритмом. Используя лобовую атаку, труднее создать произвольное сообщение, имеющее данный дайджест, если требуется порядка 2159 операций, как в случае алгоритма SHA-1, чем порядка 2127 операций, как в случае алгоритма MD5. Используя лобовую атаку, труднее создать два сообщения, имеющие одинаковый дайджест, если требуется порядка 280 как в случае алгоритма SHA-1, чем порядка 264 операций как в случае алгоритма MD5.
- Скорость: так как оба алгоритма выполняют сложение по модулю 232, они рассчитаны на 32-битную архитектуру. SHA-1 содержит больше шагов (80 вместо 64) и выполняется на 160-битном буфере по сравнению со 128-битным буфером MD5. Таким образом, SHA-1 должен выполняться приблизительно на 25% медленнее, чем MD5 на той же аппаратуре.
- Простота и компактность: оба алгоритма просты и в описании, и в реализации, не требуют больших программ или подстановочных таблиц. Тем не менее, SHA-1 применяет одношаговую структуру по сравнению с четырьмя структурами, используемыми в MD5. Более того, обработка слов в буфере одинаковая для всех шагов SHA-1, в то время как в MD5 структура слов специфична для каждого шага.
- Архитектуры little-endian и big-endian: MD5 использует little-endian схему для интерпретации сообщения как последовательности 32-битных слов, в то время как SHA-1 задействует схему big-endian. Каких-либо преимуществ в этих подходах не существует.
Хэш-функции SHA-2
В 2001 году NIST принял в качестве стандарта три хэш-функции с су-щественно большей длиной хэш-кода. Часто эти хэш-функции называют SHA-2 или SHA-256, SHA-384 и SHA-512 (соответственно, в названии ука-зывается длина создаваемого ими хэш-кода). Эти алгоритмы отличаются не только длиной создаваемого хэш-кода, но и длиной обрабатываемого блока, длиной слова и используемыми внутренними функциями. Сравним характеристики этих хэш-функций.
Таблица 3.3
Под безопасностью здесь понимается стойкость к атакам типа "парадокса дня рождения".
В SHA-256 размер блока сообщения m = 512, в SHA-384 и SHA-512 размер блока сообщения m = 1024. Каждый алгоритм оперирует с w-битными словами. Для SHA-256 w = 32, для SHA-384 и SHA-512 w = 64. В алгоритмах используются обычные булевские операции словами, а также сложение по модулю 2w, правый сдвиг на n бит SHRn(x), где х – w-битное слово, и циклические (ротационные) правый и левый сдвиги на n бит ROTRn(x)и ROTLn(x), где х – w-битное слово.
SHA-256 использует шесть логических функций, при этом каждая из них выполняется с 32-битными словами, обозначенными как x, y и z. Результатом каждой функции тоже является 32-битное слово.
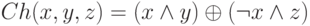
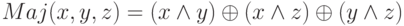
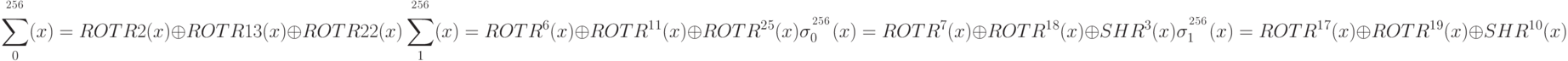
SHA-384 и SHA-512 также используют шесть логических функций, каждая из которых выполняется над 64-битными словами, обозначенными как x, y и z. Результатом каждой функции является 64-битное слово.
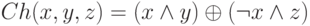
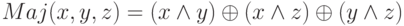

Предварительная подготовка сообщения, т.е. добавление определенных битов до целого числа блоков и последующее разбиение на блоки выполняется аналогично тому, как это делалось в SHA-1 (конечно, с учетом длины блока каждой хэш-функции). После этого каждое сообщение можно представить в виде последовательности N блоков M(1), M(2), …, M(N).
Рассмотрим SHA-256. В этом случае инициализируются восемь 32-битных переменных, которые после выполнения преобразования над очередным блоком будут являться промежуточным значением хэш-кода:
a, b, c, d, e, f, g, h
Основой алгоритма является модуль, состоящий из 64 циклических обработок каждого блока M(i):
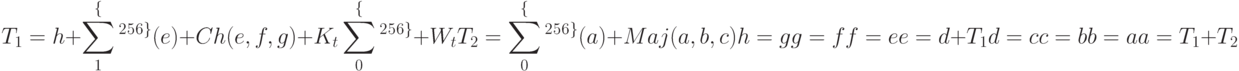
где Ki{256} – шестьдесят четыре 32-битных константы, каждая из которых является первыми 32-мя битами дробной части кубических корней первых 64 простых чисел.
Wt вычисляются из очередного блока сообщения по следующим прави-лам:
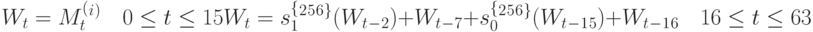
i-ое промежуточное значение хэш-кода H(t) вычисляется следующим образом:
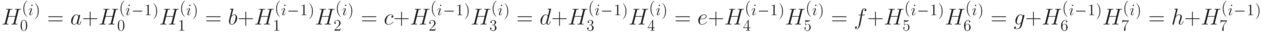
Теперь рассмотрим SHA-512. В данном случае инициализируются во-семь 64-битных переменных, которые будут являться промежуточным зна-чением хэш-кода:
a, b, c, d, e, f, g, h
Основой алгоритма является модуль, состоящий из 80 циклических обрабо-ток каждого блока M(i):
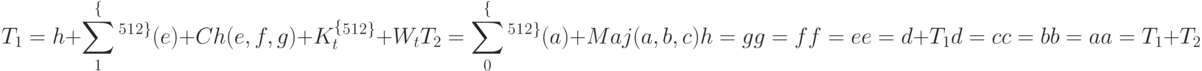
где Ki{512} – восемьдесят 64-битных констант, каждая из которых является первыми 64-мя битами дробной части кубических корней первых восьми-десяти простых чисел.
Wt вычисляются из очередного блока сообщения по следующим формулам:
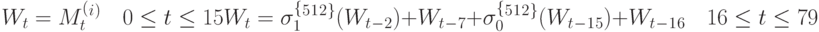
i-ое промежуточное значение хэш-кода H(t) вычисляется следующим образом:
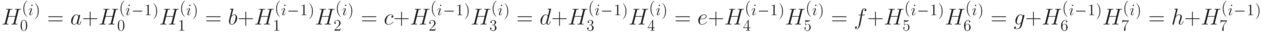
Рассмотрим SHA-384. Отличия этого алгоритма от SHA-512:
- Другое начальное значение хэш-кода H(0).
-
384-битный дайджест получается из левых 384 битов оконча-тельного хэш-кода H(N):
H0(N) || H1(N) || H2(N) || H3(N) || H4(N) || H5(N)