|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Хэш-функции и электронная подпись
9.2 Электронная подпись
9.2.3 Скрытый канал
См. [2]
Иногда требуется иметь дополнительную возможность организации скрытого канала связи в открытых сообщениях, хотя сообщения сами по себе не содержат секретной информации. В этом случаи используют скрытый канал, иногда называемый также подсознательным каналом. Подсознательный канал организуется таким образом, чтобы извлечь скрытую информацию мог только человек, обладающий секретным ключом.
Густовус Симпсон придумал идею организации подсознательного канала с помощью обычного алгоритма цифровой подписи. Так как подсознательные сообщения спрятаны в том, что выглядит нормальными цифровыми подписями, это форма маскировки. Проверяющий видит, как подписанные безобидные сообщения передаются между отправителем и получателем, но реальная передаваемая информация проходит незаметно для него по подсознательному каналу. В действительности, алгоритм подсознательного канала в подписях не отличим от нормального алгоритма в подписях. Проверяющий не только не может прочитать сообщение, передаваемое по подсознательному каналу, но у него вообще нет ни малейшего представления о существовании такового сообщения.
В общем случае организация подсознательного канала выглядит так:
- Отправитель создает безобидное сообщение;
- Используя общий ключ с получателем сообщения, отправитель подписывает безобидное сообщение, пряча свое подсознательное сообщение в подписи;
- Отправитель посылает подписанное сообщение по общедоступному каналу передачи;
- Проверяющий читает сообщение и проверяет подпись. Не обнаружив ничего подозрительного, он передает сообщение дальше;
- Получатель проверяет подпись под безобидным сообщением, убеждаясь что сообщение получено от отправителя;
- Получатель игнорирует безобидное сообщение и, используя общий с отправителем секретный ключ, извлекает подсознательное сообщение;
Рассмотрим простейший пример организации подсознательного канала передачи информации используя цифровую подпись реализуемую по методу Эль-Гамаля.
-
Сначала необходимо сгенерировать пару ключей, для этого выбирается простое
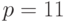 и два случайных
и два случайных  и
и 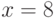 , причем
, причем 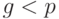 и
и 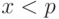 . Затем вычисляется
. Затем вычисляется 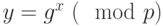 ,
,  . Открытым ключом является
. Открытым ключом является  , секретным ключом
, секретным ключом 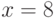 ;
; -
Создают безобидное сообщение
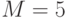 и скрытое сообщение
и скрытое сообщение 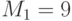 , проверяя чтобы эти сообщения были взаимно простые с
, проверяя чтобы эти сообщения были взаимно простые с  , а также чтобы
, а также чтобы  было взаимно простым c
было взаимно простым c  ; В нашем случае это так;
; В нашем случае это так; - Вычисляем значение цифровой подписи
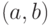

Мы получили подпись
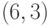 и в тоже время создали скрытый канал;
и в тоже время создали скрытый канал; - Проверяющий может просмотреть безобидное сообщение и удостовериться что сообщение передано от отправителя с подписью
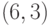 , для этого он проводит вычисления:
, для этого он проводит вычисления:

- Получатель, обладающий секретным ключом, удостоверяется в том, что сообщение пришло именно от того отправителя, с которым организован скрытый канал, для этого он проводит вычисления:

- Получатель восстанавливает скрытое сообщение:

9.2.4 Цифровая подпись на эллиптических кривых
См. [3]
В качестве международного стандарта принят американский алгоритм цифровой подписи на эллиптических кривых (ECDSA). В этом стандарте используются эллиптические кривые как над полем простого порядка, так и над полем характеристики 2. Однако криптографически стойких кривых над полем характеристики 2 сравнительно мало. Поэтому мы рассмотрим ЭЦП на эллиптических кривых, заданных над полем большей характеристики.
Замечание. В России официально принят стандарт ЭЦП на эллиптических кривых над полем большей характеристики - ГОСТ 34.10-2001 "Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи". Выбор кривой и точки на ней подразумевает решение ряда вспомогательных задач. Прежде всего, это подсчет количества точек на кривой. Если  - количество точек кривой
- количество точек кривой  над полем порядка
над полем порядка  , то должны выполняться следующие условия:
, то должны выполняться следующие условия:
 |
( 9.1) |
 |
( 9.2) |
Таким образом, чтобы отсеять лишние числа  , удовлетворяющие (9.1), можно проверять условие (9.2) для разных точек
, удовлетворяющие (9.1), можно проверять условие (9.2) для разных точек  . Единственное оставшееся число и будет искомым порядком кривой.
. Единственное оставшееся число и будет искомым порядком кривой.
На практике требуется использовать достаточно большие простые числа  . Существующие практически применимые алгоритмы [4], [5] нахождения
. Существующие практически применимые алгоритмы [4], [5] нахождения  используют аппарат алгебраической геометрии, выходящий за рамки пособия.
используют аппарат алгебраической геометрии, выходящий за рамки пособия.
Для получения криптографически стойкой системы ЭЦП должны выполняться следующие условия:
- Порядок точки
 , используемой в системе ЭЦП, должен быть простым числом
, используемой в системе ЭЦП, должен быть простым числом 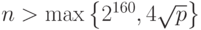 .
. -
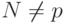 и
и 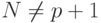 , где
, где  - порядок кривой.
- порядок кривой. -
 для всех
для всех  , где
, где  настолько велико, что вычислить дискретный логарифм в
настолько велико, что вычислить дискретный логарифм в  за приемлемое время невозможно.
за приемлемое время невозможно.
Замечание. В настоящее время значение  считается достаточным.
считается достаточным.
Возможный способ защититься от известных атак и от возможных атак для специальных классов кривых, которые могут быть обнаружены в будущем, - выбирать кривую  случайным образом так, чтобы выполнялись указанные условия.
случайным образом так, чтобы выполнялись указанные условия.
После того, как порядок  кривой определен, требуется найти большой простой делитель
кривой определен, требуется найти большой простой делитель  порядка кривой. Такой делитель может не существовать, и тогда потребуется повторять процедуру выбора кривой до тех пор, пока не будут выполнены все требуемые условия. Поиск числа
порядка кривой. Такой делитель может не существовать, и тогда потребуется повторять процедуру выбора кривой до тех пор, пока не будут выполнены все требуемые условия. Поиск числа  может потребовать как разложения на множители числа
может потребовать как разложения на множители числа  , так и доказательства простоты числа
, так и доказательства простоты числа  . Точку
. Точку  можно выбрать следующим образом. Найдем случайную точку
можно выбрать следующим образом. Найдем случайную точку 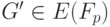 и вычислим
и вычислим 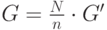 . Если
. Если  , то требуемая точка найдена, если же
, то требуемая точка найдена, если же  , то выбираем другую точку
, то выбираем другую точку 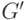 .
.
Описанные параметры могут быть общими для всех пользователей. Для генерации и проверки подписи требуются еще и индивидуальные параметры пользователя - это секретный и открытый ключи. Ключ подписи (секретный ключ) - это случайное число  ,
, 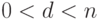 . Ключ проверки подписи (открытый ключ) - это точка эллиптической кривой
. Ключ проверки подписи (открытый ключ) - это точка эллиптической кривой 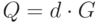 . Алгоритм ЭЦП также использует хеш-функцию, обозначаемую
. Алгоритм ЭЦП также использует хеш-функцию, обозначаемую  .
.
Генерация подписи
Входные данные: сообщение  , исходные параметры и ключ подписи. Выходные данные: подпись
, исходные параметры и ключ подписи. Выходные данные: подпись 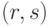 .
.
Алгоритм:
Выбрать случайное число  в интервале
в интервале 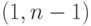 .
.
- Вычислить
 .
. - Вычислить
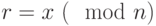 .
. - Если
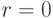 , то вернуться к шагу 1.
, то вернуться к шагу 1. - Вычислить
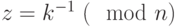 .
. - Вычислить
 .
. - Вычислить
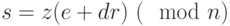 .
. - Если
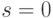 , то вернуться к шагу 1.
, то вернуться к шагу 1. - Вывести пару
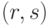 - подпись к
- подпись к  .
.
Замечания.
- При
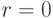 результат вычисления
результат вычисления  не зависит от секретного ключа
не зависит от секретного ключа  .
. - При
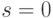 необходимого для проверки подписи числа
необходимого для проверки подписи числа  не существует.
не существует. - В качестве хеш-функции
 на 6 в стандартах ANSI X9F1 и IEEE P1363 используется SHA-1, в российском стандарте ГОСТ Р 34.10-2001~- хеширование по стандарту ГОСТ Р 34.11-94.
на 6 в стандартах ANSI X9F1 и IEEE P1363 используется SHA-1, в российском стандарте ГОСТ Р 34.10-2001~- хеширование по стандарту ГОСТ Р 34.11-94.
Пример генерации подписи
Наша цель - показать особенности алгоритма, не зависящие от разрядности чисел.
Пример 9.4 Пусть используется эллиптическая кривая  и генерирующая точка
и генерирующая точка  порядка
порядка 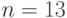 (13 - наибольший из делителей порядка кривой
(13 - наибольший из делителей порядка кривой 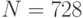 ). Предположим, абонент подписывает личным секретным ключом
). Предположим, абонент подписывает личным секретным ключом 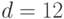 сообщение, хеш-свертка которого равна
сообщение, хеш-свертка которого равна 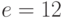 . Сгенерировать подпись.
. Сгенерировать подпись.
Пусть абонент, подписывающий сообщение, выбрал случайное  . Тогда он вычисляет
. Тогда он вычисляет  и затем
и затем  . Используя расширенный алгоритм Евклида, определяем
. Используя расширенный алгоритм Евклида, определяем  (так как
(так как 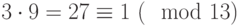 ). Наконец,
). Наконец,  . Таким образом,
. Таким образом,  - цифровая подпись данного абонента для сообщения.
- цифровая подпись данного абонента для сообщения.
В реально использующихся системах ЭЦП по российскому стандарту числа имеют порядка 60 десятичных знаков.
Проверка подписи
Входные данные: сообщение  , исходные параметры, ключ проверки подписи и подпись к
, исходные параметры, ключ проверки подписи и подпись к  .
.
Выходные данные: заключение о подлинности или фальсификации подписи.
Алгоритм:
- Если хотя бы одно из условий
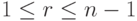 ,
,  нарушается, то подпись фальшивая и работа алгоритма закончена.
нарушается, то подпись фальшивая и работа алгоритма закончена. - Вычислить
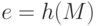 .
. - Вычислить
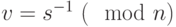 .
. - Вычислить
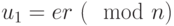 .
. - Вычислить
 .
. - Вычислить
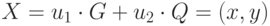 .
. - Если
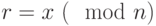 , то подпись действительная, иначе подпись фальшивая.
, то подпись действительная, иначе подпись фальшивая.
Доказательство корректности алгоритма генерации и алгоритма проверки подписи очень простое и предоставляется в качестве упражнения.
Пример 9.5 Требуется проверить подлинность подписи (11,9) для сообщения  , хэш-образ которого
, хэш-образ которого 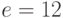 .Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен
.Секретный ключ нам неизвестен, открытый ключ абонента, подписавшего сообщение, равен 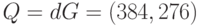 .
.
Проверка подписи начинается с проверки условий 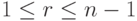 ,
, 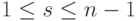 - в данном случае они соблюдаются. Затем последовательно вычисляем
- в данном случае они соблюдаются. Затем последовательно вычисляем

Находим точку

Наконец, сравниваем значения 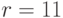 и
и  - они совпадают, следовательно, подпись действительная.
- они совпадают, следовательно, подпись действительная.
Приведем пример системы электронной подписи на эллиптической кривой, пригодный для практического применения.
Пример 9.6 Рассмотрим эллиптическую кривую

Её порядок

является простым числом, а порождающим элементом группы является точка

Для построения электронной подписи нужно выбрать закрытый ключ  и сгенерировать открытый ключ. Положим
и сгенерировать открытый ключ. Положим

Вычислим открытый ключ 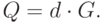

Система цифровой подписи построена.
Если читатель не имеет инструмента для работы с кривыми таких размеров, предлагаем небольшую программу на языке с++, вызывающую функцию библиотеки cryptopp для перемножение точек:
#include <iostream>
#include <cstdlib>
#include <ecp.h>
#include <integer.h>
#include <osrng.h>
using namespace std;
using namespace CryptoPP;
int main(int argc, char ** argv)
{
Integer p(argv[1]);
Integer a(argv[2]);
Integer b(argv[3]);
ECP domain(p,a,b);
Integer Gx(argv[4]);
Integer Gy(argv[5]);
ECPPoint G(Gx,Gy);
Integer OrdG(argv[6]);
ECPPoint nG = domain.Multiply(OrdG,G);
cout<<nG.x<<" "<<nG.y<<endl;
}
\end{verbatim}
Для её сборки нужно подключить библиотеку cryptopp (см. параграф 1.16.2). Допустим, мы собрали программу в исполняемый файл mulpoint (или mulpoint.exe под Windows).
Программа запускается из командной строки:
./mulpoint p a b Gx Gy d
и выводит результат через стандартный выходной поток. Например:
$ ./mulpoint 751 -1 1 384 475 3
596. 318.
(здесь $ - приглашение командной строки linux). В нашем случае, помимо 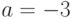 , все величины указаны в примере выше.
, все величины указаны в примере выше.
Список литературы
- Васильева И.Н. Защита информации -- СПб, 2009. -- 136 с.
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си -- М.: Триумф, 2003. -- 816 с.
- Харин Ю.С., Берник В.И., Матвеев Г.В. Математические основы криптологии -- Минск: БГУ, 1999. -- 319 с.
- Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения -- М.: УРСС, 2013.
- Schoof, R. Counting points on elliptic curves over finite fields //J. de Th\'{e}orie des Nombres de Bordeaux. -- \textnumero 7 (1995). -- p. 219-254.
- Lercier, R., Morain, F. Counting the number of points on elliptic curves over finite fields: strategies and performances,
- In L. C. Guillou and J.-J. Quisquater, editors, Advances in cryptology -- EUROCRYPT’95, \textnumero 921 (1995) of Lecture Notes in Comput. Sci. p. 79-94.
- NIST FIPS 186-4, July 2013.
