НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 8: Алгоритмы с открытыми ключами

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2513 / 558 | Длительность: 21:50:00

Специальности: Программист, Администратор информационных систем, Специалист по безопасности, Архитектор программного обеспечения, Разработчик интернет-проектов

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.5 Алгоритм Блюма-Блюма-Шуба

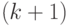Одним из наиболее стойких к криптографическим атакам является алгоритм Блюма-Блюма-Шуба (BBS). Главное его достоинство состоит в том, что строго доказано, что не существует алгоритма с полиномиальной оценкой времени его выполнения, который по любым битам выходной последовательности может предсказать ее (k+1) -й бит с вероятностью, существенно большей, чем 0,5.

Пусть и - два больших простых числа примерно одинакового размера, причем

$p{\equiv}3~(\mod 4),q{\equiv}3~(\mod 4).$

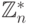Тогда число $n=\mathit{pq}$ называется целым числом Блюма. Пусть $\mathbb{Z}_n^\ast$ - мультипликативная группа кольца вычетов по модулю , $Q{R}_{n}$ - подгруппа её квадратов. Имеем:

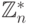$\left|\mathbb{Z}_n^\ast\right|=\varphi \left(n\right)=\left(p-1\right)\left(q-1\right),\left|Q{R}_{n}\right|=(p-1)(q-1)/4.$

Каждый квадрат из $Q{R}_{n}$ имеет ровно четыре квадратных корня в $\mathbb{Z}_n^\ast$ , и лишь один из них, называемый примитивным, лежит в $Q{R}_{n}$ .

Пример 8.11 Если 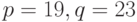, то . Тогда $133=19{\cdot}7{\notin}\mathbb{Z}_{437}^\ast$ , $135{\in}\mathbb{Z}_{437}^\ast$ , $139{\in}\mathbb{Z}_{437}^\ast$ , кроме того, учитывая, что корня из 135 по модулю 437 не существует, а ${24}^{2}=139~(\mod 437)$ , имеем:

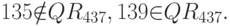
$135{\notin}Q{R}_{437},139{\in}Q{R}_{437}.$

Квадратными корнями из 139 по модулю 437 являются числа 24, 185, 252 и 413, причем 24 является примитивным, поскольку ${47}^{2}=24~(\mod 437)$ .

Задача определения примитивных квадратных корней по модулю числа вычислительно эквивалентна задаче разложения этого числа на множители. Таким образом, функция

$f\left(x\right)={x}^{2}~(\mod n)$

эффективно вычисляется, а произвести обратное преобразование может только тот, кто знает секрет - разложение f(x) на множители. Таким образом, f(x) - односторонняя функция с секретом.

Опишем теперь алгоритм генерации случайной последовательности чисел.

Пусть - целое число Блюма.

Выберем в качестве инициализирующего вектора случайное число ${x}_{0}{\in}Q{R}_{n}$ . Для этого возведём случайное число $x{\in}\mathbb{Z}_n^\ast$ в квадрат.
Искомой последовательностью битов длиной будет последовательность
$\mathit{BB}{S}_{n,m}\left({x}_{0}\right)={b}_{0}{b}_{1}{\dots}{b}_{m},$
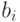где ${b}_{i}$ - младший бит числа ${x}_{i}$ ,
${x}_{i+1}={x}_{i}^{2}~(\mod n).$

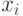Важным достоинством этого генератора является то, что при знании разложения на простые множители он допускает прямое определение отдельных битов, которые в нём вырабатываются. Имеем:

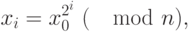
${x}_{i}={x}_{0}^{{2}^{i}}~(\mod n),$

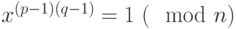причем ${x}^{(p-1)(q-1)}=1~(\mod n)$ , поэтому

${x}_{i}={x}_{0}^{{2}^{i}}~(\mod (p-1)(q-1)),$

то есть с помощью двух операций модульного возведения в степень, которые эффективно вычисляются, любое число 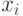${x}_{i}$ может быть найдено лишь исходя из начального вектора ${x}_{0}$ и индекса .

Термин вероятностное шифрование был введён Ш. Гольдвассер и С. Микали, и ими же была предложена первая схема такого шифрования, основанная на использовании BBS-генератора в качестве источника ключевой последовательности. Данная схема не обеспечивает секретности по отношению к атаке на основе выбранного шифртекста.

Пусть исходное сообщение - $m$-разрядная битовая последовательность, ${x}_{0}$ - случайный квадратичный вычет по модулю . Функция шифрования по схеме Гольдвассер-Микали имеет вид:

$c=\left({x}_{m},t{\oplus}\mathit{BB}{S}_{n,m}\left({x}_{0}\right)\right),$

при этом ${x}_{m}$ включается в шифртекст для того, чтобы законный получатель мог его расшифровать. При этом для расшифровки вычисляется ${x}_{0}$ по следующему алгоритму:

$\alpha &={\left(\frac{p+1}{4}\right)}^{m}~(\mod \left(p-1\right)),\\ \beta &={\left(\frac{q+1}{4}\right)}^{m}~(\mod \left(q-1\right)),\\ u&={\left({x}_{m}~(\mod p)\right)}^{\alpha }~(\mod p),\\ v&={\left({x}_{m}~(\mod q)\right)}^{\beta }~(\mod q),\\ {x}_{0}&=(apv+bqu) ~(\mod n),$

( 8.1)

где и находятся расширенным алгоритмом Евклида: ap+bq=1 .

Пример 8.12 Каждой букве русского алфавита (отождествим Е и Ё) поставим в соответствие её порядковый номер в двоичной записи:

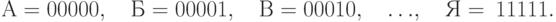
$\text{А} = 00000,\quad \text{Б} = 00001,\quad \text{В} = 00010, \quad {\dots}, \quad \text{Я} = \ 11111.$

Зашифруем слово "шифр" по алгоритму вероятностного шифрования.

Используя приведенную схему кодирования, получаем:

Выберем простые числа: 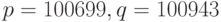p=100699,q=100943 . Тогда 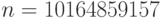n=10164859157 . Возьмём случайный квадратичный вычет ${x}_{0}=2081895771$ по модулю . Последовательно возводя его в квадрат, получаем:

	${x}_{i}$	${x}_{i}~(\mod 2)$	${t}_{i}$	${c}_{i}$
0	2081895771	1	1	0
1	3205491286	0	1	1
2	5980661497	1	0	1
3	6594526469	1	0	1
4	7854744220	0	0	0
5	7943385007	1	0	1
6	6083755268	0	1	1
7	5806084129	1	0	1
8	8344998813	1	0	1
9	10084851702	0	0	0

	${x}_{i}$	${x}_{i}~(\mod 2)$	${t}_{i}$	${c}_{i}$
10	4944625316	0	1	1
11	2015128403	1	0	1
12	3405361640	0	1	1
13	6784776583	1	0	1
14	5511098820	0	0	0
15	1025035005	1	1	0
16	5961409982	0	0	0
17	8499073980	0	0	0
18	3147729849	1	0	1
19	9863050867	1	0	1

Получаем шифртекст: c=(9863050867,01110111101111000011) .

Пример 8.13 Шифртекст получен из слова в алфавите А, Б, ..., Я по схеме вероятностного шифрования с использоваем открытого ключа 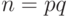. Найти открытый текст. , , .

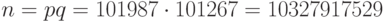Имеем m=19 , $n=pq = 101987 \cdot 101267 = 10327917529$ .

Расшифровку проведем по алгоритму (8.1):

1) Вычисляем $\alpha$ и $\beta$ :

$\alpha=\left(\frac{101987+1}{4}\right)^{19} ~ \mod (101987-1)=68875,$

$\beta=\left(\frac{101267+1}{4}\right)^{19} ~ \mod (101267-1)=48149.$

2) Находим и :

$u=(9775365428 \mod 101987)^{68875} ~ \mod 101987=101358;$

$v=(9775365428 \mod 101267)^{48149} ~ \mod 101267=25104.$

3) С помощью алгоритма Евклидва найдём целые числа и такие, что ap+bq=1 , т.е. $a=p^{-1}(\mod q)$ , $b=q^{-1}(\mod p)$ . Получаем: a=5204 , b=-5241 .

4) Находим x_0 :

$x_0=(5204\cdot 101987\cdot 25104+(-5241)\cdot 101267\cdot 101358) ~ \mod 10327917529=4034401117.$

Теперь вычисляем 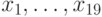$x_1, \ldots, x_{19}$ :

	${x}_{i}$	${x}_{i}~(\mod 2)$
0	4034401117	1
1	7091551751	1
2	61203754	0
3	5127594332	0
4	3464489572	0
5	6556991234	0
6	5815305655	1
7	1274312887	1
8	9344198067	1
9	2635430924	0

	${x}_{i}$	${x}_{i}~(\mod 2)$
10	8368280997	1
11	4963779332	0
12	9325316653	1
13	8084874010	0
14	9453120623	1
15	608199442	0
16	8005292144	0
17	7727784642	0
18	5896698095	1
19	9775365428	0

Прибавляя поразрядно последовательность $x_0 ~(\mod 2)$ , $x_1 ~(\mod 2)$ , $\ldots$ , $x_{19} ~(\mod 2)$ к шифрограмме, получаем код исходного сообщения:

$x_i~(\mod 2)$	11000	01110	10101	00010
шифрограмма	11010	00000	11110	01000
сумма	00010	01110	01011	01010
открытый текст	В	О	Л	К

Дальше >>

Авторизоваться

Криптографические методы защиты информации

Алгоритмы с открытыми ключами

8.5 Алгоритм Блюма-Блюма-Шуба

Вопросы и ответы