Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования
Первое применение вычислительных методов принадлежит древним египтянам, которые умели вычислять диагональ квадрата за конечное количество действий. Они также могли находить квадратный корень из 2, скорее всего, с помощью алгоритма, в дальнейшем получившего название формулы Герона, а еще позднее — метода Ньютона:
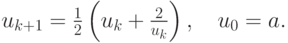
С именем среднеазиатского врача, философа и математика Аль-Хорезми связано понятие алгоритма. Разработкой вычислительных методов занимались Л.Эйлер, которому принадлежит, по-видимому, первый численный метод для решения обыкновенных дифференциальных уравнений, И.Ньютон, О.Л.Коши, Ж.Л.Лагранж, А.М.Лежандр, П.С.Лаплас, А.Пуанкаре, П.Л.Чебышёв и многие другие известные математики. Решающую роль в развитии вычислительной математики как самостоятельной науки сыграли немецкий математик Карл Рунге и русский математик, механик и кораблестроитель А.Н.Крылов.
В наше время вычислительная математика получила значительный импульс в 1950-е годы, что было связано с развитием ядерной физики, механики полета, аэродинамики спускаемых космических аппаратов. В дальнейшем решались задачи, связанные не только с расчетами действия ядерного взрыва и обтеканием боеголовок стратегических ракет. Численные методы нашли свое применение в таких областях как динамика атмосферы, термогидрография, физика плазмы, механика горных пород и ледников, синергетика, биомеханика, теория оптимизации, математическая экономика и др. Наиболее наукоемки и требуют максимальных вычислительных ресурсов задачи физики, механики и электродинамики сплошных сред. К ним относятся системы уравнений в частных производных Эйлера, Лагранжа, Максвелла и др., кинетической теории газов (уравнения Власова, Берда), а также задачи многомерной оптимизации. Развитие многих вычислительных методов — заслуга ученых, неразрывно связанных с МФТИ. Среди них следует упомянуть академиков А.А. Дородницына, О.М.Белоцерковского, А.А.Самарского, членов-корреспондентов РАН А.С.Холодова, Б.Н.Четверушкина, Ю.П.Попова, С.П.Курдюмова, профессоров В.С.Рябенького, Э.Э.Шноля, Р.П.Федоренко, Л.А.Чудова, В.Ф.Дьяченко, И.М.Гельфанда, Г.А.Тирского, А.П.Фаворского.
Вычислительная математика отличается от других математических дисциплин и обладает специфическими особенностями.
- Вычислительная математика имеет дело не только с непрерывными, но и с
дискретными объектами. Так, вместо отрезка прямой часто рассматривается система
точек
 , вместо непрерывной функции f(x) — табличная функция
, вместо непрерывной функции f(x) — табличная функция 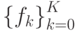 , вместо первой производной — ее разностная аппроксимация, например,
, вместо первой производной — ее разностная аппроксимация, например,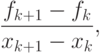

Такие замены, естественно, порождают погрешности метода.
- В машинных вычислениях присутствуют числа с ограниченным количеством
знаков после запятой из-за конечности длины мантиссы при представлении действительного числа в памяти ЭВМ. Другими словами, в вычислениях присутствует машинная погрешность (округления)
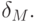 Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в
математическом анализе.
Это приводит к вычислительным эффектам, неизвестным, например, в классической теории обыкновенных дифференциальных уравнений, уравнений математической физики или в
математическом анализе. - В вычислительной практике большое значение имеет обусловленность задачи, т.е. чувствительность ее решения к малым изменениям входных данных.
- В отличие от "классической" математики выбор вычислительного алгоритма влияет на результаты вычислений.
- Существенная черта численного метода — экономичность вычислительного алгоритма, т.е. минимизация числа элементарных операций при выполнении его на ЭВМ.
- Погрешности при численном решении задач делятся на две категории — неустранимые и устранимые. К первым относят погрешности, связанные с построением математической модели объекта и приближенным заданием входных данных, ко вторым — погрешности метода решения задачи и ошибки округления, которые являются источниками малых возмущений, вносимых в решение задачи.
Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.
