|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Быстрая одноквантовая логика
Введение
С использованием переходов Джозефсона (ПД) предложено много вариантов логических элементов, с помощью которых можно организовать быстрые компьютерные вычисления. Мы рассмотрим здесь лишь один из наилучших вариантов, который в англоязычных публикациях называют "Rapid Single-Flux-Quantum" или сокращенно "RSFQ". В русскоязычной литературе этот вариант называют "быстрой одноквантовой логикой" или сокращенно "БОК логикой".
Динамические свойства перехода Джозефсона
Чтобы объяснить принципы действия БОК логики, рассмотрим сначала детальнее динамические свойства ПД. В предыдущей лекции (
рис.
2.4) описана стационарная ампер-вольтная характеристика ПД, которую можно построить при условии, что через ПД пропускается калиброванный электрический ток  . Рассмотрим теперь случай, когда кроме постоянного электрического тока смещения
. Рассмотрим теперь случай, когда кроме постоянного электрического тока смещения  , несколько меньшего, чем критический ток
, несколько меньшего, чем критический ток 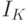 , (
рис.
2.1 слева) на ПД в какой-либо момент времени
, (
рис.
2.1 слева) на ПД в какой-либо момент времени 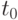 действует очень короткий импульс напряжения ( справа вверху).
Его амплитуда должна быть достаточна для того, чтобы суммарный ток через ПД превысил
действует очень короткий импульс напряжения ( справа вверху).
Его амплитуда должна быть достаточна для того, чтобы суммарный ток через ПД превысил 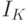 . В интервале времени, когда ток через ПД превышает критическое значение
. В интервале времени, когда ток через ПД превышает критическое значение 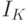 , на переходе появляется падение напряжения
, на переходе появляется падение напряжения  и согласно уравнению (2.6) предыдущей лекции происходит быстрое изменение фазы сверхпроводящего тока. Когда входное напряжение исчезает, электрический ток через возбужденный ПД еще относительно долго продолжает колебаться (штриховая кривая 1), постепенно затухая до стационарного значения
и согласно уравнению (2.6) предыдущей лекции происходит быстрое изменение фазы сверхпроводящего тока. Когда входное напряжение исчезает, электрический ток через возбужденный ПД еще относительно долго продолжает колебаться (штриховая кривая 1), постепенно затухая до стационарного значения  .
.

Рис. 2.1. Слева – ампер-вольтная характеристика ПД; справа вверху – короткий импульс напряжения, внизу – динамическая реакция тока через ПД на этот импульс: 1 и 2 – при отсутствии и при наличии демпфирования, 3 – при значительном демпфировании
Если ПД демпфировать, добавляя элемент, частично поглощающий энергию колебаний, то колебания затухают быстрее (кривая 2). Если же добавить элемент, который быстро поглощает энергию колебаний, то колебания исчезают совсем (пунктирная кривая 3). Оказалось, что этого легко достичь шунтированием ПД пленочным проводником, изготовленным из не сверхпроводящего металла. Такой шунт практически не влияет на свойства ПД в сверхпроводящем состоянии, а при выходе из сверхпроводящего состояния принимает на себя лишь часть избыточного (сверх 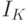 ) тока. Для построения логических элементов важным является то, что шунтированный таким образом ПД переключается очень быстро – за единицы пикосекунд, а при наноразмерах – и еще быстрее.
) тока. Для построения логических элементов важным является то, что шунтированный таким образом ПД переключается очень быстро – за единицы пикосекунд, а при наноразмерах – и еще быстрее.
БОК триггер
Динамические свойства шунтированного ПД эффективно используются в быстрой одноквантовой логике. Опишем сначала схему и способ функционирования БОК триггера. На рис. 2.2 показана принципиальная электрическая схема т.н. R-S-триггера. Условные изображения шунтированного ПД и сверхпроводящих шин показаны справа в рамках, обведенных штриховыми линиями. Для сверхпроводящих шин такое изображение выбрано потому, что их импеданс носит в основном индуктивный характер.
Основой R-S-триггера является сквид, образованный двумя шунтированными переходами Джозефсона ПД1 и ПД2 и замкнутым сверхпроводящим контуром  . Как вы уже знаете, суммарный магнитный поток сквозь отверстие такого контура всегда должен быть кратным кванту магнитного потока
. Как вы уже знаете, суммарный магнитный поток сквозь отверстие такого контура всегда должен быть кратным кванту магнитного потока 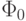 . Базовое состояние сквида, когда в сверхпроводящем контуре незатухающий ток
. Базовое состояние сквида, когда в сверхпроводящем контуре незатухающий ток  циркулирует против часовой стрелки, принимают за логический "0", а когда ток циркулирует по часовой стрелке, – за логическую "1". На сквид подается ток смещения
циркулирует против часовой стрелки, принимают за логический "0", а когда ток циркулирует по часовой стрелке, – за логическую "1". На сквид подается ток смещения  , подобранный так, чтобы оба эти состояния были стабильными.
, подобранный так, чтобы оба эти состояния были стабильными.

Рис. 2.2. Принципиальная схема R-S-тригера – одного из основных элементов БОК логики (справа в штриховых рамках расшифрованы условные изображения)
R-S-триггер имеет два входа, которые принято называть R– и S-входами. Вход R соединен с ПД2 через сверхпроводящую шину L1 и ПД3, а вход S соединен с ПД1 через сверхпроводящую шину L2 и ПД2. Выходной сигнал берется с перехода Джозефсона ПД2 через сверхпроводящую шину L3.
Триггер функционирует следующим образом. Пусть сначала он находится в состоянии "0". В этом состоянии через ПД1 течет ток  , близкий к критическому току
, близкий к критическому току 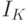 , а через ПД2 течет ток
, а через ПД2 течет ток  , далекий от критического тока. Когда на вход S действует короткий импульс напряжения, вызванный им дополнительный ток не приводит к превышению критического тока в переходах Джозефсона ПД2 и ПД4, но вызывает превышение его в переходе ПД1. Из-за этого сверхпроводящее состояние здесь на короткое время разрушается, и в контур сквида "просачивается" квант магнитного потока. Направление циркуляции тока в контуре изменяется на противоположное, и сквид переходит в состояние "1". Поскольку ПД2 остается в сверхпроводящем состоянии, напряжение на выходе не появляется.
, далекий от критического тока. Когда на вход S действует короткий импульс напряжения, вызванный им дополнительный ток не приводит к превышению критического тока в переходах Джозефсона ПД2 и ПД4, но вызывает превышение его в переходе ПД1. Из-за этого сверхпроводящее состояние здесь на короткое время разрушается, и в контур сквида "просачивается" квант магнитного потока. Направление циркуляции тока в контуре изменяется на противоположное, и сквид переходит в состояние "1". Поскольку ПД2 остается в сверхпроводящем состоянии, напряжение на выходе не появляется.
Если импульс напряжения действует на вход S, когда триггер находится в состоянии "1", то к приходу импульса через ПД1 течет ток  . Параметры ПД4 подобраны так, что в этом случае сверхкритический ток возникает именно в нем, однако связанный с этим квант магнитного потока действует извне и не просачивается в контур сквида. Поэтому состояние сквида в этом случае не изменяется.
. Параметры ПД4 подобраны так, что в этом случае сверхкритический ток возникает именно в нем, однако связанный с этим квант магнитного потока действует извне и не просачивается в контур сквида. Поэтому состояние сквида в этом случае не изменяется.
Переход сквида из состояния "1" в состояние "0" может произойти лишь при поступлении импульса напряжения на вход R. В этом случае сверхкритический ток возникает на переходе ПД2. При этом из контура сквида "вытекает" квант магнитного потока, направление циркуляции тока в контуре изменяется на противоположное, и сквид переходит в состояние "0". На выходе триггера появляется кратковременный импульс напряжения.
Если ОК импульс поступает на вход R, когда триггер находится в состоянии "0", то через ПД2 течет ток  . Параметры перехода Джозефсона ПД3 (как и ПД4) подобраны так, что в этом случае сверхкритический ток возникает именно в нем. Однако связанный с этим квант магнитного потока тоже действует извне и не просачивается в контур сквида. Поэтому состояние сквида ПД2 в этом случае не изменяется, и на выходе не возникает импульс напряжения.
. Параметры перехода Джозефсона ПД3 (как и ПД4) подобраны так, что в этом случае сверхкритический ток возникает именно в нем. Однако связанный с этим квант магнитного потока тоже действует извне и не просачивается в контур сквида. Поэтому состояние сквида ПД2 в этом случае не изменяется, и на выходе не возникает импульс напряжения.
Как видим, ОК импульс может появиться на выходе R-S-триггера только в состоянии "1" при появлении одноквантового импульса на его входе R. Это и используется при построении схем БОК логики.
Если ни на один из входов импульс не поступает, то состояние сквида не изменяется и на выходе ОК импульс не появляется. Это называют "режимом хранения информации". Одновременное поступление импульсов на оба входа считается запрещенным, так как следующее состояние сквида становится в таком случае неопределенным.
Вследствие закона Джозефсона (3.6) между импульсом напряжения на ПД и квантом магнитного потока сквозь замкнутый контур существует соотношение
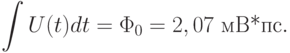 |
( 2.1) |
В этом смысле (по величине "площади" импульса) выходной импульс напряжения всегда "стандартный". Его принято называть одноквантовым импульсом напряжения или сокращенно ОК импульсом. Он является вполне достаточным для надежного переключения следующих звеньев в логической сети обработки цифровой информации.

