|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Информационная безопасность. Стандарты и алгоритмы шифрования
Алгоритм шифрования RSA
Алгоритм RSA предполагает, что посланное закодированное сообщение может быть прочитано адресатом и только им. В этом алгоритме используется два ключа — открытый и секретный. Данный алгоритм привлекателен также в случае, когда большое число субъектов (N) должно общаться по схеме все-со-всеми. В случае симметричной схемы шифрования каждый из субъектов каким-то образом должен доставить свои ключи всем остальным участникам обмена, при этом суммарное число используемых ключей будет достаточно велико при большом значении N. Применение асимметричного алгоритма требует лишь рассылки открытых ключей всеми участниками, суммарное число ключей равно N (см. RFC-2437).
Сообщение представляется в виде числа M. Шифрование осуществляется с помощью общедоступной функции f(M), и только адресату известно, как выполнить операцию f-1 (дешифрацию) Адресат выбирает два больших простых числа p и q, которые делает секретными. Он объявляет n=pq и число e, c (e,p-1)=(e,q-1)=1 (e,p-1) и (e,q-1) – наибольший общий делитель для e и р-1 (соответственно e и q-1 ). Один из возможных способов выполнить это условие, выбрать e больше чем p/2 и q/2 ). Комбинация n и e представляет собой открытый ключ. Шифрование производится по формуле:
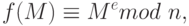
где M и f(M) оба <= n-1. Такое преобразование может быть выполнено за разумное время, даже если M, e и n содержит весьма большое число знаков. Адресат вычисляет M на основе Me, используя свое знание p и q.
Исходный текст M получается адресатом из зашифрованного f(M) путем преобразования:
M = (f(M))d (mod n).
Здесь как исходный текст, так и зашифрованный рассматриваются как длинные двоичные числа. Значение d вычисляется из e, если известны p и q, на основе соотношения.
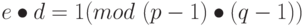
Так как (Me)d - M делимо на p и q, оно делимо и на pq, следовательно, мы можем определить M, зная Md, вычислив его значение в степени e и определив остаток от деления на pq. Для соблюдения секретности важно, чтобы, зная n, было нельзя вычислить p и q. Если n содержит 100 цифр, подбор шифра связан с перебором ~1050 комбинаций. Данная проблема изучается уже около 100 лет. RSA -алгоритм запатентован (20 сентября 1983, патент действовал до 2000 года).
Теоретически можно предположить, что возможно выполнение операции f-1, не вычисляя p и q. Но в любом случае задача эта не проста и разработчики считают ее трудно факторизуемой.
Предположим, что мы имеем зашифрованный текст f(M) и исходный текст M, и мы хотим найти значения p и q. Нетрудно показать, что таких исходных данных для решения задачи недостаточно — надо знать все возможные значения Mi.
Поясним использование алгоритма RSA на конкретном примере. Выбираем два простые числа p=7; q=17 (на практике эти числа во много раз длиннее). В этом случае n = p*q будет равно 119. Теперь необходимо выбрать e, выбираем e=5. Следующий шаг связан с формированием числа d так, чтобы d*e=1 mod [(p-1)(q-1)]. d=77 (использован расширенный алгоритм Эвклида). d — секретный ключ, а e и n характеризуют открытый ключ. Пусть текст, который нам нужно зашифровать, представляется M=19. С = Memod n. Получаем зашифрованный текст C=66. Этот "текст" может быть послан соответствующему адресату. Получатель дешифрует полученное сообщение, используя М=Cdmod n и C=66. В результате получается M=19.
На практике общедоступные ключи могут помещаться в специальную базу данных. При необходимости послать партнеру зашифрованное сообщение можно сделать сначала запрос его открытого ключа. Получив его, можно запустить программу шифрации, а результат ее работы послать адресату. На использовании общедоступных ключей базируется и так называемая электронная подпись, которая позволяет однозначно идентифицировать отправителя. Сходные средства могут применяться для предотвращения внесения каких-либо корректив в сообщение на пути от отправителя к получателю. Быстродействующие аппаратные 512-битовые модули могут обеспечить скорость шифрования на уровне 64 кбит в сек. Готовятся ИС, способные выполнять такие операции со скоростью 1 Мбайт/сек. Разумный выбор параметра e позволяет заметно ускорить реализацию алгоритма.
Стандарт шифрования AES
Стандарт AES (Advanced Encryption Standard) является стандартом шифрования США, принятым в 2000 году. Он специфицирует алгоритм Rijndael http://www.nist.gov/CryptoToolkit (смотри также http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf). Этот алгоритм представляет собой симметричный блочный шифр, который работает с блоками данных длиной 128 бит и использует ключи длиной 128, 192 и 256 бит (версии AES-28; AES-192 и AES-256). Сам алгоритм может работать и с другими длинами блоков данных и ключей, но эта возможность в стандарт не вошла.
Биты данных нумеруются с нуля, начиная со старших. В AES основным является полиномиальное представлением кодов. Так, байт { 01100011 } следует представлять как: x6 +x5 + x + 1.
Алгоритм AES производит операции над двумерными массивами байт, называемыми структурами (state). Структура состоит из 4 рядов по Nb байт. Nb равно длине блока, деленной на 32 (в данном стандарте Nb=4 ). Это позволяет обозначать структуру как sr,c или s[r,c], где 0<=r<4 и 0<=c<4.
Входной код (in), который является последовательностью 16 байт можно представить как:
s[r,c] =in[r +4c]
При реализации алгоритма AES используются операции сложения байт (по модулю 2 = XOR) и умножения. В алгоритме AES при умножении байтов используется неприводимый многочлен:
m(x) = x8 + x4 + x3 + x + 1Пример 1.
Вычисление произведения М байтов {b1} на {b2} здесь выполняется согласно следующему алгоритму:
![M=[\{ b1\} \bullet \{ b2\} ]\ mod\ m(x).](/sites/default/files/tex_cache/537bb8dde6e3c74d0094f0a7f75a9086.png)
В этом случае обратная величина байта равна:
{b}-1 ={b} mod m(x)
Пример
3.
для умножения полубайтов (коды длиной 4 бита) используется неприводимый полином:
m2(x) = x4 + 1Пример 4.
Вычисление произведения М полубайтов {a} на {b} здесь выполняется следующим образом:
![M=[\{ a\} \bullet \{ b\} ]\ mod\ m_{2}(x).](/sites/default/files/tex_cache/04241e1ae2eb9876fd8a59165915c3a0.png)
M представляет собой полубайт d. Операцию умножения полубайтов {a} на {b} можно записать в матричном виде:
![\left[\begin{array}{c}d_0\\d_1\\d_2\\d_3\end{array}\right]=\left[\begin{array}{c}a_0a_3a_2a_1\\a_1a_0a_3a_2\\a_2a_1a_0a_3\\a_3a_2a_1a_0\end{array}\right]\left[\begin{array}{c}b_0\\b_1\\b_2\\b_3\end{array}\right]](/sites/default/files/tex_cache/e578291fcf01881f02e47a42e0bb8990.png)
Как было сказано выше, длины ключей Nk (длина, измеренная в 32 битных словах) могут принимать значения 4, 6 или 8 (для AES-128, -192 и -256, соответственно). Число итераций Nr (round), реализуемых в алгоритме AES составляет соответственно 10, 12 и 14.
