Типы данных

Использование стека

Будем рассматривать последовательности открывающихся и закрывающихся круглых и квадратных скобок ( ) [ ]. Среди всех таких последовательностей выделим правильные - те, которые могут быть получены по таким правилам:

• пустая последовательность правильна.
• если A и B правильны, то и AB правильна.
• если A правильна, то [ A ] и ( A ) правильны.

Пример. Последовательности (), , правильны, а последовательности ], )(, (], ([)] - нет.

6.1.1. Проверить правильность последовательности за время, не превосходящее константы, умноженной на ее длину. Предполагается, что члены последовательности закодированы числами:

Решение. Пусть - проверяемая последовательность. Разрешим хранить в стеке открывающиеся круглые и квадратные скобки (т. е. 1 и 2).

Вначале стек делаем пустым. Далее просматриваем члены последовательности слева направо. Встретив открывающуюся скобку (круглую или квадратную), помещаем ее в стек. Встретив закрывающуюся, проверяем, что вершина стека - парная ей скобка; если это не так, то можно утверждать, что последовательность неправильна, если скобка парная, то заберем ее (вершину) из стека. Последовательность правильна, если в конце стек оказывается пуст.

Сделать_пустым (s);
i := 0; Обнаружена_ошибка := false;
{прочитано i символов последовательности}
while (i < n) and not Обнаружена_ошибка do begin
| i := i + 1;
| if (a[i] = 1) or (a[i] = 2) then begin
| | Добавить (a[i], s);
| end else begin  {a[i] равно -1 или -2}
| | if Пуст (s) then begin
| | | Обнаружена_ошибка := true;
| | end else begin
| | | Взять (t, s);
| | | Обнаружена_ошибка := (t <> - a[i]);
| | end;
| end;
end;
Правильно := (not Обнаружена_ошибка) and Пуст (s);

Убедимся в правильности программы.

(1) Если последовательность построена по правилам, то программа даст ответ "да". Это легко доказать индукцией по построению правильной последовательности. Надо проверить для пустой, для последовательности AB в предположении, что для A и B уже проверено, и, наконец, для последовательностей [A] и (A) - в предположении, что для A уже проверено. Для пустой очевидно. Для AB действия программы происходят как для A и кончаются с пустым стеком; затем все происходит как для B. Для [A] сначала помещается в стек открывающая квадратная скобка и затем все идет как для A - с той разницей, что в глубине стека лежит лишняя скобка. По окончании A стек становится пустым - если не считать этой скобки - а затем и совсем пустым. Аналогично для (A).

(2) Покажем, что если программа завершает работу с ответом "да", то последовательность правильна. Рассуждаем индукцией по длине последовательности. Проследим за состоянием стека в процессе работы программы. Если он в некоторый промежуточный момент пуст, то последовательность разбивается на две части, для каждой из которых программа дает ответ "да"; остается воспользоваться предположением индукции и определением правильности. Пусть стек все время непуст. Это значит, что положенная в него на первом шаге скобка будет вынута лишь на последнем шаге. Тем самым, первый и последний символы последовательности - это парные скобки, и последовательность имеет вид (A) или [A], а работа программы (кроме первого и последнего шагов) отличается от ее работы на A лишь наличием лишней скобки на дне стека (раз ее не вынимают, она никак не влияет на работу программы). Снова ссылаемся на предположение индукции и определение правильности.

6.1.2. Как упростится программа, если известно, что в последовательности могут быть только круглые скобки?

Решение. В этом случае от стека остается лишь его длина, и мы фактически приходим к такому утверждению: последовательность круглых скобок правильна тогда и только тогда, когда в любом ее начальном отрезке число закрывающихся скобок не превосходит числа открывающихся, а для всей последовательности эти числа равны.

6.1.3. Реализовать с помощью одного массива два стека, суммарное количество элементов в которых ограничено длиной массива; все действия со стеками должны выполняться за время, ограниченное константой, не зависящей от длины стеков.

Решение. Стеки должны расти с концов массива навстречу друг другу: первый должен занимать места

6.1.4. Реализовать k стеков с элементами типа T, общее количество элементов в которых не превосходит n, с использованием массивов суммарной длины 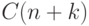, затрачивая на каждое действие со стеками (кроме начальных действий, делающих все стеки пустыми) время не более некоторой константы . (Как говорят, общая длина массивов должна быть 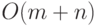, a время на каждую операцию - .)

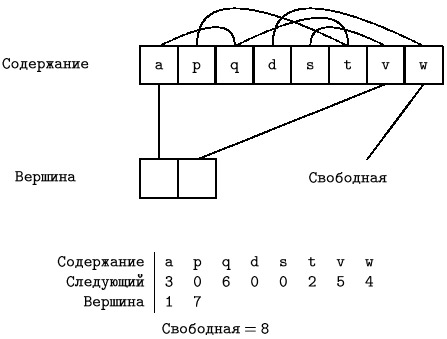
Решение. Применяемый метод называется "ссылочной реализацией". Он использует три массива:

Содержание: array [1..n] of T;
Следующий: array [1..n] of 0..n;
Вершина: array [1..k] of 0..n.

Удобно изображать массив Содержание как n ячеек с номерами 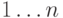, каждая из которых содержит элемент типа T. Массив Следующий изобразим в виде стрелок, проведя стрелку из i в j, если Следующий[i]=j. (Если Следующий[i]=0, стрелок из i не проводим.) Содержимое s -го стека ( 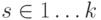) хранится так: вершина равна Содержание[Вершина[s]], остальные элементы s -го стека можно найти, идя по стрелкам - до тех пор, пока они не кончатся. При этом

Стрелочные траектории, выходящие из

Стеки: 1-ый содержит p, t, q, a ( a - вершина); 2-ой содержит s, v ( v - вершина).

procedure Начать_работу; {Делает все стеки пустыми}
| var i: integer;
begin
| for i := 1 to k do begin
| | Вершина [i]:=0;
| end;
| for i := 1 to n-1 do begin
| | Следующий [i] := i+1;
| end;
| Следующий [n] := 0;
| Свободная:=1;
end;

function  Есть_место: boolean;
begin
| Есть_место := (Свободная <> 0);
end;

procedure Добавить (t: T; s: integer);
| {Добавить t к s-му стеку}
| var i: 1..n;
begin
| {Есть_место}
| i := Свободная;
| Свободная := Следующий [i];
| Следующий [i] := Вершина [s];
| Вершина [s] :=i;
| Содержание [i] := t;
end;

function Пуст (s: integer): boolean;
| {s-ый стек пуст}
begin
| Пуст := (Вершина [s] = 0);
end;

procedure Взять (var t: T; s: integer);
| {взять из s-го стека в t}
| var i: 1..n;
begin
| {not Пуст (s)}
| i := Вершина [s];
| t := Содержание [i];
| Вершина [s] := Следующий [i];
| Следующий [i] := Свободная;
| Свободная := i;
end;

function  Вершина_стека (s: integer): T;
| {вершина s-го стека}
begin
| Вершина_стека := Содержание[Вершина[s]];
end;