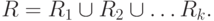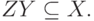Методы проектирования логических моделей реляционных баз данных. Декомпозиция и синтез отношений
Декомпозиция схем отношений, свойства соединения без потерь и сохранения ФЗ
Одной из целей проектирования реляционной базы данных является построение декомпозиции (разбиения) универсального отношения на совокупность отношений, удовлетворяющих требованиям нормальных форм.
Введем определение декомпозиции схемы отношения.
Определение 1. Декомпозицией схемы отношений
называется замена ее совокупностью
подмножества R, таких, что
Прежде чем перейти к изучению метода декомпозиции схем отношений, рассмотрим проблему соединения отношений при разбиении универсального отношения. Когда мы заменяем исходное отношение на два других взаимосвязанных отношения, правомерно предположить, что эти отношения будут представлять собой проекции исходного отношения на соответствующие атрибуты. Единственный способ выяснить, содержат ли полученные проекции ту же информацию, что и исходное отношение, - восстановить ее, выполнив естественное соединение полученных проекций. Если отношение, полученное в результате выполнения соединения, не будет совпадать с исходным отношением, то невозможно сказать, какое из них является первоначальным отношением для данной схемы. Таким образом, проблема заключается в том, что при соединении можно потерять существующие или приобрести ранее не существовавшие ложные кортежи. Рассмотрим пример декомпозиции с потерей информации.
Атрибуты А и В не зависят функционально от атрибута С.
Говорят, что декомпозиция 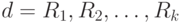 схемы отношения r обладает свойством соединения без потерь относительно множества ФЗ D, если каждое отношение R, удовлетворяющее D, может быть представлено в виде:
схемы отношения r обладает свойством соединения без потерь относительно множества ФЗ D, если каждое отношение R, удовлетворяющее D, может быть представлено в виде:

Пусть  Тогда для отображений проекции-соединения справедливы следующие свойства:
Тогда для отображений проекции-соединения справедливы следующие свойства:
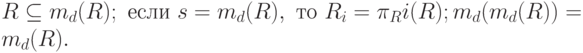
Эти свойства следуют из определения естественного соединения. Первое свойство используется при проверке, обладает ли декомпозиция свойством соединения без потерь относительно некоторого множества ФЗ.
Рассмотрим алгоритм проверки свойства соединения без потерь.
Алгоритм. Проверка декомпозиции на свойство соединения без потерь
input: схема отношения R(A1, A2, ..., Ak), множество ФЗ F,
декомпозиция d={R1, R2, ..., Rk}.
output: Булева переменная истина или ложь.Алгоритм
- Построим таблицу с n столбцами и k строками, где столбец j соответствует атрибуту Аj, а строка i - схеме отношения Ri. На пересечении строки i и столбца j поместим символ aj, если атрибут Aj принадлежит Ri. В противном случае поместим символ bij.
- Многократно просматриваем каждую ФЗ из F, до тех пор, пока внесение изменений в таблицу станет невозможным. Просматривая зависимость
 ищем строки, которые совпадают по всем столбцам, соответствующим атрибутам из Х. При обнаружении таких строк отождествляем их символы в столбцах, соответствующих атрибутам из Y, по правилу aj в aj, bij в bij.
ищем строки, которые совпадают по всем столбцам, соответствующим атрибутам из Х. При обнаружении таких строк отождествляем их символы в столбцах, соответствующих атрибутам из Y, по правилу aj в aj, bij в bij. - Если после модификации строк таблицы оказывается, что некоторая строка равна a1, a2, ..., ak, то декомпозиция d обладает свойством соединения без потерь. В противном случае декомпозиция d таким свойством не обладает.
Приведенный алгоритм позволяет корректно определить, обладает ли декомпозиция свойством соединения без потерь.
Рассмотрим пример применения алгоритма, используя отношение ПОСТАВКИ (Поставщик, Адрес, Товар, Стоимость). Обозначим его атрибуты как: А - поставщик, В - адрес, C - товар, D - стоимость, при этом имеют место ФЗ 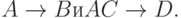
Пример. Проверка декомпозиции на свойство соединения без потерь
Схема отношения 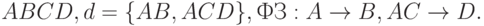
Поскольку имеет место 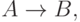 и две строки совпадают по А, то можно отождествить их символы для А: b22 на a2. В итоге имеем таблицу
и две строки совпадают по А, то можно отождествить их символы для А: b22 на a2. В итоге имеем таблицу
Вывод. Декомпозиция d обладает свойством соединения без потерь.
При декомпозиции одной схемы отношения на две другие схемы отношений используется более простая проверка: декомпозиция обладает свойством соединения без потерь, если только 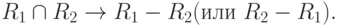 Такая ФЗ должна принадлежать F+.
Такая ФЗ должна принадлежать F+.
Свойство соединения без потерь гарантирует, что любое отношение может быть восстановлено из его проекций. Понятно, что при декомпозиции ФЗ исходной схемы отношения распределяются по новым отношениям. Поэтому важно, чтобы при декомпозиции множество ФЗ F для схемы отношения r было выводимым из проекций на схемы Ri.
Введем следующее определение.
Определение 2. Проекцией множества ФЗ F на множество атрибутов Х, обозначаемой
называется множество ФЗ
в F+, таких, что
Говорят, что декомпозиция обладает свойством сохранения ФЗ, если из объединения всех ФЗ, принадлежащих 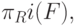 логически следуют все зависимости из F.
логически следуют все зависимости из F.
Рассмотрим отношение (Город, Адрес, Почтовый_индекс). Обозначим его атрибуты как: А - город, В - адрес, C - почтовый индекс, при этом имеют место ФЗ 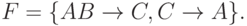 Декомпозиция схемы этого отношения ABC на AC и BC обладает свойством соединения без потерь, поскольку верна ФЗ
Декомпозиция схемы этого отношения ABC на AC и BC обладает свойством соединения без потерь, поскольку верна ФЗ  Однако проекция на BC дает только тривиальные зависимости, проекция на АС дает ФЗ
Однако проекция на BC дает только тривиальные зависимости, проекция на АС дает ФЗ 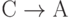 и тривиальные ФЗ. Из ФЗ
и тривиальные ФЗ. Из ФЗ 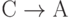 не следует зависимость
не следует зависимость 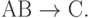 Поэтому данная декомпозиция не сохраняет ФЗ, хотя и обладает свойством соединения без потерь.
Поэтому данная декомпозиция не сохраняет ФЗ, хотя и обладает свойством соединения без потерь.
Рассмотрим пример нарушения ФЗ при декомпозиции.
Пример. Нарушение ФЗ при декомпозиции
R1 (B, C) R2(A, C)
Лесная, 6 132432 Черноголовка, МО 132432
Лесная, 6 132431 Черноголовка, МО 132431
R(A, B, C)
Черноголовка, МО 132432 Лесная, 6
Черноголовка, МО 132431 Лесная, 6
R = R1>< R2, для R2 справедлива С \to А, для R не справедлива АВ \ to С.С другой стороны, декомпозиция может обладать свойством сохранения ФЗ, но не обладать свойством соединения без потерь. Например, 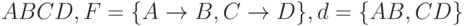
Таким образом, с точки зрения теории реляционных баз данных хорошая схема отношений реляционной базы данных должна по возможности отвечать следующим требованиям:
- исключать избыточное дублирование;
- исключать потенциальную противоречивость данных;
- обладать свойством соединения без потерь;
- обладать свойством сохранения ФЗ.
В процессе нормализации исходной схемы отношений, задаваемых информационной моделью данных, должны быть получены схемы отношений, отвечающие вышеперечисленным требованиям.