Массивы
Системы линейных уравнений
Рассмотрим систему из n линейных уравнений с n неизвестными:
 |
( 6.8) |
В матричном виде эта система записывается намного элегантнее:
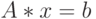 |
( 6.9) |
Здесь вектор неизвестных x рассматривается как столбец - прямоугольная матрица размерности n*1. Аналогичный вид имеет вектор правых частей b системы уравнений. В матричном виде условие существования решения системы линейных уравнений 6.8 и нахождение самого решения формулируется совсем просто. Для существования решения необходимо и достаточно, чтобы определитель матрицы A был отличен от нуля. Тогда у матрицы A существует обратная матрица 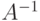 . Для нахождения решения системы умножим обе части уравнения 6.9 на
. Для нахождения решения системы умножим обе части уравнения 6.9 на 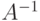 . Тогда получим:
. Тогда получим:
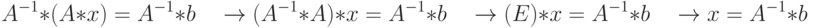 |
( 6.10) |
Для нахождения решения системы линейных уравнений, матрица которой имеет определитель, отличный от нуля, достаточно вычислить обратную матрицу и умножить ее на вектор правых частей системы уравнений.
Если нужно решить m систем линейных уравнений с одной и той же матрицей  , но с разными правыми частями, то обратную матрицу достаточно вычислить один раз. В матричном виде решение m систем линейных уравнений
, но с разными правыми частями, то обратную матрицу достаточно вычислить один раз. В матричном виде решение m систем линейных уравнений
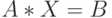
задается соотношением:
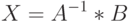
Здесь  - прямоугольная матрица размерности
- прямоугольная матрица размерности 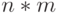 , каждый столбец которой представляет вектор правых частей одной системы уравнений. Соответствующий столбец матрицы
, каждый столбец которой представляет вектор правых частей одной системы уравнений. Соответствующий столбец матрицы  дает решение этой системы. Что произойдет, если в качестве матрицы
дает решение этой системы. Что произойдет, если в качестве матрицы  рассмотреть единичную матрицу? Очевидно, что тогда матрица
рассмотреть единичную матрицу? Очевидно, что тогда матрица  будет представлять собой обратную матрицу
будет представлять собой обратную матрицу 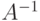 . Несмотря на кажущуюся очевидность соотношения
. Несмотря на кажущуюся очевидность соотношения 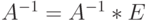 , в нем есть определенный смысл, который постараюсь сейчас прояснить. Три задачи - вычисление определителя, решение системы линейных уравнений, нахождение обратной матрицы - имеют одинаковую вычислительную сложность и требуют, если не применять специальные алгоритмы, выполнения порядка
, в нем есть определенный смысл, который постараюсь сейчас прояснить. Три задачи - вычисление определителя, решение системы линейных уравнений, нахождение обратной матрицы - имеют одинаковую вычислительную сложность и требуют, если не применять специальные алгоритмы, выполнения порядка 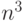 операций умножения и сложения.
Если посмотреть на соотношение 6.10, то кажется, что решить систему уравнений несколько сложнее, чем вычислить обратную матрицу, поскольку нужно вначале найти обратную матрицу, а затем умножить ее на вектор правых частей
операций умножения и сложения.
Если посмотреть на соотношение 6.10, то кажется, что решить систему уравнений несколько сложнее, чем вычислить обратную матрицу, поскольку нужно вначале найти обратную матрицу, а затем умножить ее на вектор правых частей  . Однако реальный алгоритм, рассматриваемый ниже и находящий решение системы, вычислительно проще, чем тот же алгоритм, находящий обратную матрицу. Для такого алгоритма найти обратную матрицу - это все равно, что решить n систем линейных уравнений с одной и той же матрицей
. Однако реальный алгоритм, рассматриваемый ниже и находящий решение системы, вычислительно проще, чем тот же алгоритм, находящий обратную матрицу. Для такого алгоритма найти обратную матрицу - это все равно, что решить n систем линейных уравнений с одной и той же матрицей  в левой части, используя матрицу
в левой части, используя матрицу  в качестве правых частей.
в качестве правых частей.
Алгоритм Гаусса
Рассмотрим сейчас алгоритм Гаусса, позволяющий найти решение всех интересующих нас задач - вычислить определитель матрицы, решить m систем линейных уравнений, найти обратную матрицу. Построим вначале расширенную матрицу 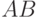 , состоящую из двух клеток:
, состоящую из двух клеток:
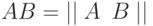
Матрица  , дополняющая матрицу
, дополняющая матрицу  , зависит от того, какую задачу предполагается решить. Если нужно вычислить только определитель матрицы
, зависит от того, какую задачу предполагается решить. Если нужно вычислить только определитель матрицы  , то расширенная матрица совпадает с исходной и матрица
, то расширенная матрица совпадает с исходной и матрица  в этом случае отсутствует. Если нужно решить одну систему линейных уравнений, то матрица
в этом случае отсутствует. Если нужно решить одну систему линейных уравнений, то матрица  состоит из одного столбца - правых частей системы уравнений. Если нужно решить m систем уравнений, то матрица
состоит из одного столбца - правых частей системы уравнений. Если нужно решить m систем уравнений, то матрица  состоит из
состоит из  векторов, каждый из которых задает правые части своей системы уравнений. Если нужно найти обратную матрицу, то матрица
векторов, каждый из которых задает правые части своей системы уравнений. Если нужно найти обратную матрицу, то матрица  задается единичной матрицей
задается единичной матрицей  .
.
После того, как построена расширенная матрица, вся специфика конкретной задачи теряется - над расширенной матрицей выполняются одни и те же действия с параллельным вычислением определителя матрицы  . В чем суть этих действий? Над матрицей
. В чем суть этих действий? Над матрицей 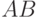 последовательно выполняются элементарные преобразования - деление элементов строки на число, что изменяет величину определителя, и вычитание из одной строки матрицы другой строки, умноженной на некоторое число. Цель наших действий состоит в том, чтобы в расширенной матрице
последовательно выполняются элементарные преобразования - деление элементов строки на число, что изменяет величину определителя, и вычитание из одной строки матрицы другой строки, умноженной на некоторое число. Цель наших действий состоит в том, чтобы в расширенной матрице 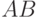 клетку
клетку  преобразовать в единичную матрицу
преобразовать в единичную матрицу  . Поскольку каждое элементарное действие можно рассматривать, как умножение слева на некоторую матрицу, совокупность преобразований, переводящая
. Поскольку каждое элементарное действие можно рассматривать, как умножение слева на некоторую матрицу, совокупность преобразований, переводящая  в
в  , эквивалентна умножению слева на матрицу
, эквивалентна умножению слева на матрицу 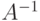 .
Но это означает также, что эти преобразования переводят клетку
.
Но это означает также, что эти преобразования переводят клетку  в матрицу
в матрицу 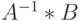 , что и дает решение исходных задач. Поскольку в результате преобразования
, что и дает решение исходных задач. Поскольку в результате преобразования  переходит в единичную матрицу, определитель которой известен и равен 1, а для каждого преобразования известно, как меняется величина определителя, параллельно вычисляется и величина определителя исходной матрицы
переходит в единичную матрицу, определитель которой известен и равен 1, а для каждого преобразования известно, как меняется величина определителя, параллельно вычисляется и величина определителя исходной матрицы  .
.
Рассмотрим на простом примере матричный вид элементарных операций. Пусть элементарная операция состоит в том, что к первой строке прибавляется вторая строка, умноженная на число  . Это действие эквивалентно умножению почти единичной матрицы на исходную матрицу:
. Это действие эквивалентно умножению почти единичной матрицы на исходную матрицу:
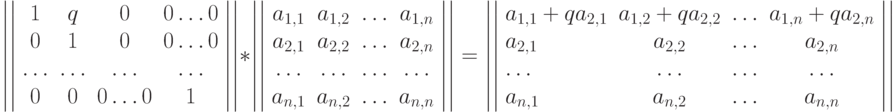
Матрица, задающая элементарную операцию, отличается от единичной матрицы тем, что у нее в первой строке на втором месте стоит число q, а не ноль. Если бы к первой строке прибавлялась не вторая строка, а строка с номером j, то число q стояло бы не на втором месте, а в позиции j. Если строка j прибавляется не к первой строке, а к строке с номером i, то число q появлялось бы в i-ой строке матрицы.
Рассмотрим теперь возможную реализацию алгоритма Гаусса:
public void Gauss(double[,] M)
{
det = 1;
int n = M.GetLength(0);
int m = M.GetLength(1);
double d =0,r=0;
for (int i = 0; i < n; i++)
{
//Приведение столбца i к единичному вектору
d = M[i, i]; det *= d;
//деление на диагональный элемент: M[i,i]теперь = 1;
for (int k = 0; k < m; k++)
M[i, k] /= d;
//Элементарная операция: сложение строк
for (int j=0; j<n; j++)
{
//К строке j прибавляется строка i, умноженная на r
//В результате M[j,i]=0
if(j!=i)
{
r=-M[j,i];
for (int k = 0; k < m; k++)
M[j, k] += r * M[i, k];
}
}
}Аргументом метода является расширенная матрица  . В результате работы метода матрица
. В результате работы метода матрица  приобретает вид:
приобретает вид: 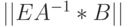 . В зависимости от того, как задана матрица B, находится решение одной системы уравнений, нескольких систем или вычисляется значение обратной матрицы. Параллельно в переменной det формируется значение определителя матрицы A.
. В зависимости от того, как задана матрица B, находится решение одной системы уравнений, нескольких систем или вычисляется значение обратной матрицы. Параллельно в переменной det формируется значение определителя матрицы A.
Алгоритм Гаусса в том виде, как он выше рассмотрен, не всегда обеспечивает получение результата. Действительно, пусть в матрице А элемент a[1,1] равен нулю. Тогда при выполнении элементарных операций в процессе преобразования матрицы А к единичной матрице Е возникнет ошибка уже на первом шаге при делении первой строки на элемент a[1,1]. Однако равенство нулю диагонального элемента вовсе не означает, что определитель матрицы равен нулю (если речь не идет о диагональной матрице) или что для нее не существует обратной матрицы.
Возможны различные модификации рассматриваемого алгоритма, исправляющие ситуацию.
Алгоритм с выбором первого ненулевого элемента
В случае, когда а[i, i] равно нулю, алгоритм ищет первую строку ниже i-й, в которой элемент a[i, j] не равен нулю. Эта строка добавляется к строке i, что гарантирует возможность деления на а[i, i].
Алгоритм с выбором главного элемента в столбце
Прежде чем приводить столбец к единичному виду, алгоритм ищет в столбце максимальный по модулю элемент и меняет местами строку i и строку j, в которой находится максимальный элемент. При обмене строк может измениться знак определителя матрицы.
Алгоритм с выбором главного элемента во всей матрице
На каждом шаге приведения очередного столбца к диагональному виду в еще не приведенной матрице отыскивается максимальный элемент и меняются местами не только строки, но и столбцы матрицы, ставя максимальный элемент в позицию а[i, i]. Этот прием гарантирует отсутствие переполнения при выполнении операции деления. Гарантируется также, что при умножениях не будет получено слишком большое число, поскольку деление на максимальный элемент с последующим умножением на один из элементов приводит к тому, что элементы преобразованной матрицы не увеличиваются по модулю. Однако ничто не дается даром. Выбор главного элемента, перестановка строк и столбцов, необходимость обратной перестановки в конце вычислений - все это усложняет алгоритм. Как правило, страдает и точность вычислений, особенно для плохо обусловленных матриц. Все модификации алгоритма стоит применять тогда, когда в основной схеме возникла исключительная ситуация, требующая корректировки алгоритма. Обработчик исключительной ситуации при делении на ноль, возникновении переполнения, потере значащих цифр может вызывать модифицированный вариант алгоритма в надежде получить решение, когда отказывается работать основная схема.
Замечу, что никакая модификация не может помочь найти обратную матрицу, если она не существует и определитель матрицы действительно равен нулю. В этом случае, например, все элементы в столбце, начиная с диагонального и ниже его, будут равны нулю. Это и будет означать, что определитель матрицы равен нулю, обратная матрица и решение системы уравнений не существует.
Интерполяционный полином, определитель Вандермонда и обусловленность матриц
Вернемся к задаче построения интерполяционного полинома, проходящего через заданное множество точек. Напомню, заданы своими координатами 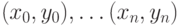 точки, через которые должен пройти полином степени n. Требуется найти коэффициенты
точки, через которые должен пройти полином степени n. Требуется найти коэффициенты 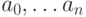 этого полинома. Ранее был рассмотрен алгоритм Лагранжа, позволяющий построить этот полином. Нетрудно понять, что существует прямое решение этой задачи, состоящее в построении системы линейных уравнений для нахождения неизвестных коэффициентов полинома. В матричном виде эта система уравнений имеет вид:
этого полинома. Ранее был рассмотрен алгоритм Лагранжа, позволяющий построить этот полином. Нетрудно понять, что существует прямое решение этой задачи, состоящее в построении системы линейных уравнений для нахождения неизвестных коэффициентов полинома. В матричном виде эта система уравнений имеет вид:
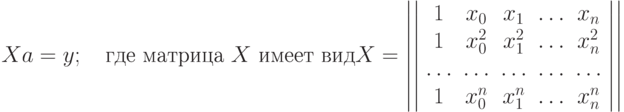
Матрица X называется матрицей Вандермонда, а ее определитель - соответственно, определителем Вандермонда. Этот определитель вычисляется достаточно просто:
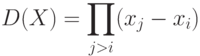
Он равен произведению разностей координат точек, где произведение берется по всем j, большим i. Очевидно, что определитель будет отличен от нуля, если у точек нет совпадающих координат x. Этот факт отмечался и при рассмотрении полинома Лагранжа, когда говорилось, что множество точек "не имеет возвратов".
Когда определитель матрицы равен нулю, то, как уже говорилось, не существует обратной матрицы и нельзя найти решение системы линейных уравнений. Для системы линейных уравнений это означает, что уравнения в ней являются линейно зависимыми и одно из них представляет линейную комбинацию других уравнений. Такая система не обладает полной информацией и не может использоваться для однозначного нахождения решения.
На практике часто возникает ситуация, когда матрица системы появляется в результате измерений, ее элементы представляют не точные значения, а содержат ошибки измерений. Здесь система уравнений может иметь определитель, отличный от нуля, но быть "почти" линейно зависимой в пределах ошибок измерений. В таких случаях формально найденное решение может быть далеким от "истинного" решения. Как правило, матрица подобных систем является плохо обусловленной, а сама система уравнений называется неустойчивой. Дадим более точное определение. Матрица А называется плохо обусловленной, а система уравнений - неустойчивой, если малым изменениям элементов прямой матрицы соответствуют большие изменения в обратной матрице. Понятно, что если обратная матрица вычислена с большими ошибками, то и решение системы содержит ошибки такого же порядка.
Если матрица А плохо обусловлена, то и обратная к ней также является плохо обусловленной матрицей. Во сколько раз могут возрастать ошибки в элементах прямой матрицы при ее обращении? Примерный ответ на это дают "числа обусловленности" матрицы. Предлагаются различные количественные меры обусловленности матриц. Одной из таких мер является М-число обусловленности Тьюринга:
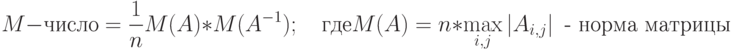
Матрица Вандермонда - потенциальный кандидат на плохую обусловленность. Если посмотреть на ее структуру, то видно, что для ее элементов во многих случаях характерен большой размах - отношение между максимальным и минимальным элементом велико. Действительно, пусть, например, максимальная по модулю координата 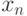 имеет значение 100, а степень полинома n равна 6. Это довольно скромные цифры, но уже в этом случае минимальный элемент матрицы равен 1, а максимальный -
имеет значение 100, а степень полинома n равна 6. Это довольно скромные цифры, но уже в этом случае минимальный элемент матрицы равен 1, а максимальный - 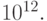 Примерно такой же размах будет и у элементов обратной матрицы. Ее максимальный элемент будет примерно равен 1, а минимальный -
Примерно такой же размах будет и у элементов обратной матрицы. Ее максимальный элемент будет примерно равен 1, а минимальный - 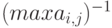 , так что число обусловленности M будет примерно равно
, так что число обусловленности M будет примерно равно 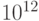 . При наличии небольших ошибок в измерении координат ошибки в определении значений полинома в точках, отличных от измеряемых, могут многократно возрастать. По этой причине интерполяционный полином еще можно применять
внутри интервала измерений, но не рекомендуется использовать в задачах экстраполяции.
. При наличии небольших ошибок в измерении координат ошибки в определении значений полинома в точках, отличных от измеряемых, могут многократно возрастать. По этой причине интерполяционный полином еще можно применять
внутри интервала измерений, но не рекомендуется использовать в задачах экстраполяции.
Проект
- 48. Построить проект, включающий построение интерфейса пользователя и класса LinAlgebra. Методы класса должны реализовать все алгоритмы, рассмотренные в этом разделе. Интерфейс пользователя должен позволять пользователю решать основные задачи, возникающие при работе матрицами, определителями, системами линейных уравнений.
