Переменные, присваивание и ссылки
Использование ссылок для моделирования связанных структур данных
Еще одно, уже продемонстрированное приложение ссылок состоит в представлении коллекции объектов, называемой также "контейнером" объектов. Коллекцию можно рассматривать как совокупность связанных ячеек, каждая из которых может содержать ссылки на другие ячейки. Примером может служить связный список, такой как наша линия метро, последовательная структура, где каждая ячейка, кроме последней, содержит ссылку right на следующий элемент.
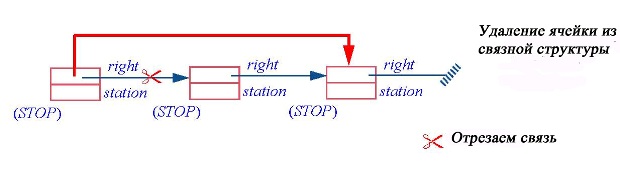
Связные структуры облегчают выполнение таких операций, как вставка и удаление. Для примера удалим из мини-линии метро второй элемент, указав новую связь для right-ссылки. Эффект операции показан на рисунке:
Рассмотрим возможную для класса STOP-процедуру, представляющую удаление следующей остановки на линии:
remove_right
— Удаление следующей остановки.
require
not_last: right /= Void
do
right: = right.right
ensure
skipped_one: right = old right.right
end
Альтернативой мог бы быть метод, в котором удалено предусловие, изменен заголовочный комментарий "— Удаление следующей остановки, если она имеется" и изменено тело процедуры следующим образом:
if right /= Void then right := right.right end
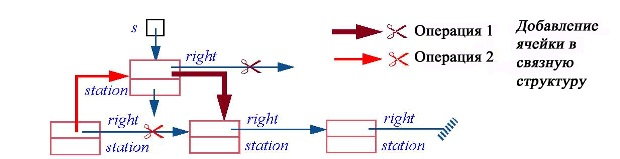
Аналогично, мы могли бы пожелать вставить еще одну остановку между текущей и следующей, если таковая имеется:
Вот соответствующий метод (предполагается, что он должен быть добавлен к классу STOP):
put_right (s: STOP)
— Добавить к линии метро остановку s после текущей остановки,
— оставляя любые последующие остановки.
require
exists: s /= Void
do
s.link (right) — Операция 1
right := s — Операция 2
ensure
linked_to_new: right = s
retained_others: right.right = old right
end
Метод работает независимо от того, присоединена ли righ1 к объекту или имеет значение void (текущая остановка является последней). Новая ячейка s не должна быть пустой. Предыдущее значение ее right-ссылки, каково оно ни было — пусто или присоединено, будет потеряно при выполнении метода link, но station станция, с ней связанная, останется.
Как и в алгоритме свопинга — обмена данными двух значений — порядок присваивания важен. Мы связываем s с ее новым соседом (операция 1 на рисунке), представленным полем right, в его исходном значении. Только после этого можно изменить значение right, применяя операцию 2.
Процедуры remove_right и put_right иллюстрируют общие схемы манипуляции со связанными структурами.
В большинстве практических случаев интерфейс будет слегка отличен. Операции вставки не будет передаваться в качестве аргумента элемент списка, такой как STOP-объект в нашем примере. Вместо этого аргументом будет объект типа STATION, после чего в методе будет создан элемент списка с присоединенной станцией и вновь созданный элемент будет вставлен в список. Мы будем изучать такие операции при обсуждении связных списков.
Void ссылки
Третье преимущество ссылок предоставляет значение Void, используемое, в частности, для завершения связанных структур, символически изображенное на последних рисунках.
Как вы знаете, этот благословенный дар опасен: возможность, что объект v имеет значение void на некотором шаге некоторого сеанса выполнения, усложняет программирование, требуя проверки цели каждого вызова v.f (...), поскольку необходимо гарантировать, что v никогда не будет void при любом выполнении вызова.
Это и есть та цена, которую приходится платить за гибкость описания связанных структур данных. Сопроводим эту ситуацию методологическим советом.
Почувствуй методологию
Резервируйте void-ссылки для завершения связанных структур.
Это означает, что не следует использовать void для представления специальных значений типов, не задающих связанные структуры. Например, создавая класс ACCOUNT в программе, моделирующей работу с банковскими счетами, не следует использовать void для представления ошибочного счета, лучше создать специальный объект — "Неизвестный_счет". Это избавит вас от риска вызова метода класса ссылкой со значением void. Конечно, необходимо позаботиться о разборе ситуации, когда встречается специальный объект, поскольку вы также не хотите, чтобы метод выполнялся, но давал неправильные результаты.
Обращение списка
Процедуры remove_right и put_right дают хороший пример работы со связанными структурами. Их простые, но уже не тривиальные алгоритмы демонстрируют заботу о void-значениях.
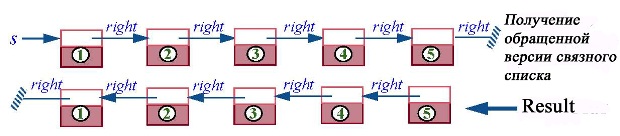
Для дальнейшего знакомства со ссылочными алгоритмами давайте рассмотрим более сложный в реализации алгоритм обращения списка. Чтобы не слишком усложнять задачу, будем рассматривать задачу создания нового списка, элементы которого связаны в обратном порядке по отношению к исходному списку:
Мы начинаем с s — ссылки на линию метро. Так как каждая остановка метро имеет ссылку на следующую остановку, можно, используя s, получить доступ ко всей линии, последовательно применяя right. Мы не хотим модифицировать эту структуру, но хотим создать новую, доступную через Result в нашей функции, которая будет содержать те же элементы, но сцепленные в обратном порядке. Для иллюстрации на рисунке показана информация, связанная с каждым STOP-объектом (станции, заданные также ссылками, представлены номерами от 1 до 5).
Всякий раз, когда предлагается некоторая задача, разумно перед дальнейшим чтением попытаться самому найти ее решение.
В таких алгоритмах важна производительность. Первый элемент нового списка является последним элементом исходного списка, поэтому для его получения нужно пройти весь исходный список. Для получения второго элемента снова нужно пройти исходный список до предпоследнего элемента. Это плохая стратегия, требующая порядка n2 операций, если в списке n элементов. Вместо этого мы хотим выполнить обращение списка, проходя исходный список лишь один раз.
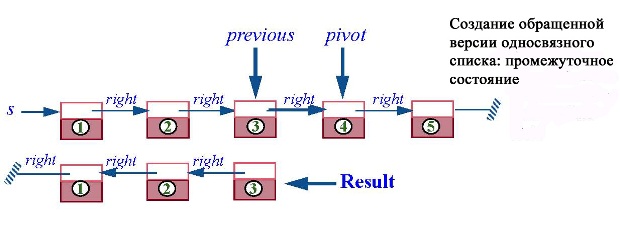
Как для любого итеративного алгоритма, ключом для нахождения правильного алгоритма или для понимания существующего алгоритма, является инвариант цикла, задающий свойства на каждом шаге цикла. Рисунок ниже показывает ситуацию, возникающую на одной из итераций пока еще не написанного цикла.
Вот что мы сделаем для получения обращенной формы части исходного списка. Введем две переменные — они будут локальными переменными метода, которые будут показывать, насколько мы продвинулись по исходному циклу:
- previous указывает на последнюю ячейку, уже включенную в обращенный список;
- pivot указывает на первую еще не обработанную ячейку, получая значение void, когда мы обработаем все ячейки исходного цикла. Так что условие pivot = Void будет сигнализировать, что мы все сделали, и может служить условием выхода из цикла.
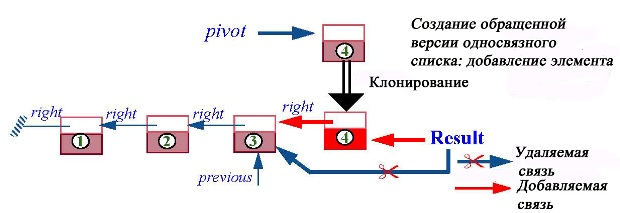
Эти два свойства задают инвариант цикла. Схема простая. На каждой итерации цикла обрабатывается следующая ячейка, известная как pivot. Создается клон этой ячейки, который и добавляется в новый список, становясь его началом, что нетрудно сделать, зная Result, ссылку на начало списка. После этого в исходном списке передвигаются вправо previous и pivot, что восстанавливает истинность инварианта. Вот описание метода:
reversed (s: STOP): STOP
— Новая остановка - первая на новой линии, имеющей те же станции,
— что и s, но идущие в обратном порядке.
— Нет предусловия, поскольку метод работает и для s, представляющей
— пустой список.
local
previous, pivot: STOP
do
from
previous := Void; pivot := s
invariant
— Список с началом Result содержит все ячейки исходного списка
— от начала и до previous включительно; pivot задает следующую
— ячейку, если она есть.
until
pivot = Void
loop
Result := pivot.cloned; Result.link (previous)
previous := pivot; pivot := pivot.right
variant
— Смотри ниже.
end
end
Нам необходима локальная переменная previous для сохранения предыдущего значения pivot на момент создания новой ячейки. Для инициализации previous используется значение Void. Вызов функции cloned позволяет создать новый объект (аналогично оператору создания), дублирующий поле за полем объекта a.
В зависимости от используемой версии библиотеки для тех же целей может использоваться twin, старое имя cloned.
На рисунке показаны детали добавления ячейки.
Следует убедиться, что алгоритм всегда применяет квалифицированные вызовы pivot.cloned и pivot.right в теле цикла с непустым pivot.
При изучении рекурсии появится интересное упражнение, требующее переписать метод reversed с использованием рекурсии вместо цикла.