|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Теория перегрузки
Пример такой системы показан на рис.9.1, где мы рассматриваем иерархическую сеть с нагрузкой от А до В и от А до С. От А до В есть прямой (первичный) маршрут с  каналами. Если они все заняты, то вызов направляется по альтернативному (вторичному) маршруту через Т к В. Подобным же образом, нагрузка от А до С имеет маршрут первого выбора, т.е. направление А С, и альтернативный маршрут АТС. Предположим, что маршруты ТВ, и ТС не имеют потерь; схема доступности показана в правой части рис.9.1. На этом рисунке мы видим, что общее количество каналов
каналами. Если они все заняты, то вызов направляется по альтернативному (вторичному) маршруту через Т к В. Подобным же образом, нагрузка от А до С имеет маршрут первого выбора, т.е. направление А С, и альтернативный маршрут АТС. Предположим, что маршруты ТВ, и ТС не имеют потерь; схема доступности показана в правой части рис.9.1. На этом рисунке мы видим, что общее количество каналов  и что нагрузка АВ имеет доступ только к
и что нагрузка АВ имеет доступ только к  . В этом случае последовательный поиск среди маршрутов должен быть организован так, чтобы з
апрос был направлен через группу
. В этом случае последовательный поиск среди маршрутов должен быть организован так, чтобы з
апрос был направлен через группу  только тогда, когда все
только тогда, когда все  первичных каналов заняты.
первичных каналов заняты.
Это типично для иерархической сети, которая обладает такой сервисной защитой. Независимо от того, насколько высока будет нагрузка от А до С, мы никогда не получим доступ к  каналам.
каналам.
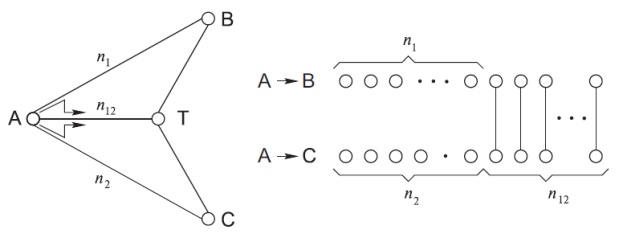
Рис. 9.1. Телекоммуникационные сети с обходным маршрутом и соответствующей схемой доступности, которая названа транспонированием О'Делла (O'Dell).
Мы предполагаем, что линии связи между транзитной станцией T и станции В и С - без потерь. Каналы 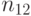 являются общими для обоих потоков нагрузки.
являются общими для обоих потоков нагрузки.
С другой стороны, мы можем потерять вызовы, даже если есть свободные каналы, и поэтому использование каналов в этой системе всегда будет ниже, чем для систем с полной доступностью, но больше, чем для полностью раздельных систем с таким же общим количеством каналов. Каналы общего пользования в неполнодоступной системе дают возможность как-то сбалансировать нагрузку между этими двумя группами.
Исторически было необходимо поговорить об ограниченной доступности, так как электромеханические системы очень ограничивали возможности управления и емкость коммутатора (доступность). В цифровых системах мы не имеем этих ограничений но, тем не менее, теория ограниченной доступности важна в сетях и при гарантии уровня обслуживания.
Теория перегрузки
Классические модели нагрузки принимают, что нагрузка, предлагаемая системе - чистая случайная нагрузка,типа один, РСТ1, или нагрузка типа два, РСТ2. В сетях связи с альтернативной маршрутизацией нагрузка, которая потеряна первичной группой, предлагается группе перегрузки, и она имеет свойства, отличающие её от РСT -нагрузки (секция 6.4). Поэтому мы не можем использовать классические модели для того, чтобы оценить вероятности блокировки нагрузки в группе перегрузки.
Пример 9.1.1: Разделение одной группы на две
Рассмотрим группу с 16-ю каналами, которым предлагается нагрузка 10 Эрл. РСТ 1. Применив В-формулу Эрланга, мы находим вероятность блокировки Е = 2,23 % и потерянную нагрузку 0,2230 Эрл.
Теперь используем последовательный поиск и разбиваем эти 16 каналов на первичную группу, и группу перегрузки, каждая из 8 каналов.
Применив В формулу Эрланга, находим, что нагрузка перегрузки от первичной группы равняется 3,3832Эрл. Эта нагрузка предлагается группе перегрузки. Используя снова В формулу Эрланга, находим потерянную нагрузку от группы перегрузки: 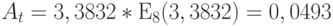 Эрл.
Эрл.
Полная вероятность блокировки при этом способе становится 0,49 3 %, это намного меньше, чем результат 2,23 % для общего пучка. Мы сделали ошибку, применяя В-формулу к нагрузке перегрузки, которая не является РСТ 1 нагрузкой. Далее мы приводим два класса моделей для расчета нагрузки перегрузки. Можно, в принципе, изучать процесс обработки нагрузки либо вертикально, либо горизонтально. При вертикальном изучении вычисляются вероятности состояния (секции 9.1.1-9.4.3). При горизонтальном изучении анализируются расстояние между двумя прибытиями вызовов, то есть межинтервальным распределением времени (9.5).
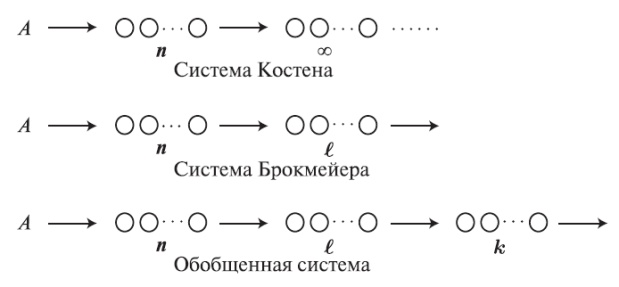
Вероятность состояния систем перегрузки
Рассмотрим полнодоступную группу с упорядоченным (последовательным поиском). Группа разбита на ограниченную первичную группу с п каналами и группой перегрузки с бесконечной емкостью, предлагаемая нагрузка - РСТ I. Это называется системой Костена (рис.9.2). Состояние системы описывается двухмерным вектором:
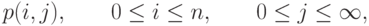 |
( 9.1) |
это является вероятностью, что в случайный момент времени заняты в первичной группе i каналов, и j каналов в группе перегрузки. Диаграмма переходов состояний показана на рис.9.3. Костен (1937 [68]) проанализировал эту модель и получил безусловные вероятности состояний:
 |
( 9.2) |
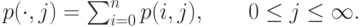 |
( 9.3) |
Риордан (Riordan 1956 [87]) получил моменты безусловных (одномерных) распределений, среднюю величину и пиковость (отношение дисперсия/средняя величина) безусловных (одномерных) распределений, то есть характеристики нагрузки, которую обслуживают эти две группы.
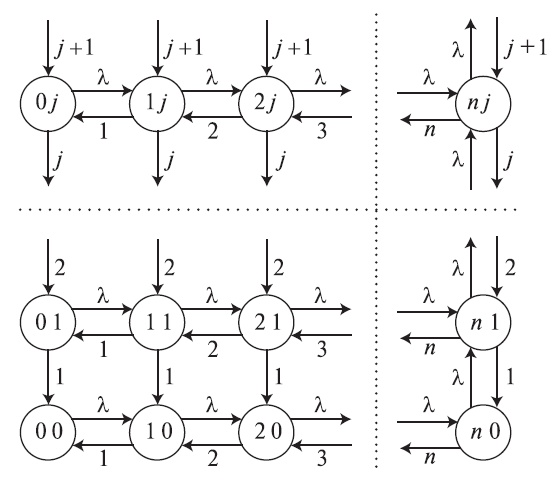
Рис. 9.3. Диаграмма переходов состояний для системы Костена, которая имеет первичную группу с п каналами, и неограниченную группу перегрузки. Состояние обозначено (i,j), где I-число занятых каналов в первичной группе, и j - число занятых каналов в группе перегрузки. Среднее время пребывания в системе выбрано как единица времени.
Первичная группа:
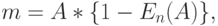 |
( 9.4) |
 |
( 9.5) |
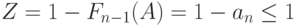
где 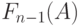 - функция увеличения В-формулы Эрланга.
- функция увеличения В-формулы Эрланга.
Вторичная группа - это группа перегрузки:
 |
( 9.6) |
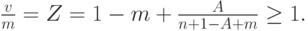 |
( 9.7) |
Опыт показывает, что пиковость Z - удачная характеристика для относительной вероятности блокировки, которая хорошо отображает поток нагрузки с данной средней величиной. На рис.9.4 можно видеть, что пиковость нагрузки перегрузки имеет максимум для фиксированной нагрузки и увеличивает число каналов. Пиковость имеет размерность [каналы]. Пиковость применима для теоретических вычислений, но трудно оценить ее точно с помощью наблюдений.
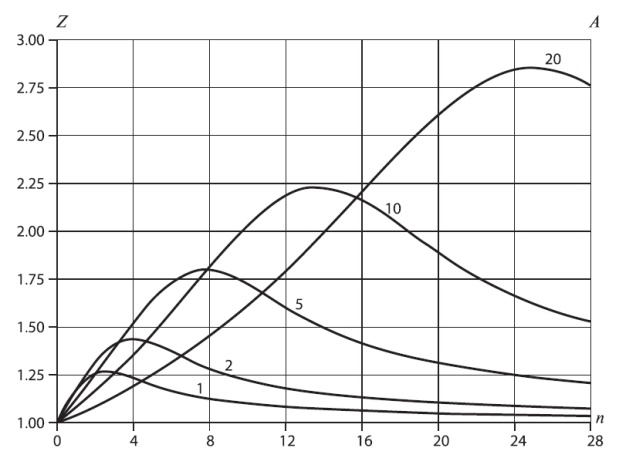
Рис. 9.4. Пиковость Z нагрузки перегрузки как функция числа каналов для фиксированного значения предложенной нагрузки. Заметьте, что Z имеет максимум. Когда п становится большим, попытки вызова редко блокируются, а блокированные попытки взаимно независимы. Поэтому процесс увеличения вызовов сходится к Пуассоновскому процессу (Лекция 6)
Для РСТ 1 пиковость нагрузки равна единице, а блокировка вычисляется по В-формуле Эрланга. Если пиковость меньше, чем единица (9.5), нагрузка называется сглаженной, и она меньше блокируется, чем нагрузка РСT 1. Если пиковость больше единцы, то нагрузка называется взрывной, и она больше блокируется, чем нагрузка РСТ 1. Нагрузка перегрузки обычно взрывная (9.7).
Брокмейер (1954 [10]) получил вероятности состояния и моменты системы с ограниченной группой перегрузки (рис. 9.2), которые названы системой Брокмейера.
Беч (Been 1954 [6]) сделал то же самое, используя матричные уравнения, и получил более сложные и более общие выражения. Шерер (Sherer) вывел моменты более высокого порядка для конечных групп перегрузки, обобщающие систему Брокмейера.
Валстрем (Wallstroml966 [101]) рассчитал вероятности состояния и моменты для нагрузки перегрузки обобщенной системы Костена, где интенсивность прибытия зависит или от общего количества вызовов в системе, или от числа вызовов в первичной группе.
Метод эквивалентной случайной нагрузки
Этот метод также называется ERT (equivalent Random Traffic) - метод Уилкинсона, изданным независимо в одно и то же время в США Уилкинсом (1956 [102]) и в Германии Бретшнайдером (1956 [8]). Он играет ключевую роль для измерения характеристик телекоммуникационных сетей.
Предварительный анализ
Рассмотрим группу с l каналами, которая обслуживает g потоков нагрузки (рис.9.5). Потоки нагрузки могут быть, например, нагрузкой, которая предлагается от других станций транзитной станции, и поэтому классические модели нагрузки не могут описать их. Таким образом, мы не знаем распределения (вероятности состояния) потоков нагрузки, но можем (как это часто происходит в приложениях статистики) характеризовать i -тый поток нагрузки его средней величиной  и дисперсией
и дисперсией 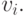 С этим упрощением мы будем предполагать, что два потока нагрузки будут эквивалентными, если они имеют ту же самую среднюю величину (математическое ожидание) и дисперсию. Полная нагрузка, предлагаемая группе с l каналами, имеет среднюю величину:
С этим упрощением мы будем предполагать, что два потока нагрузки будут эквивалентными, если они имеют ту же самую среднюю величину (математическое ожидание) и дисперсию. Полная нагрузка, предлагаемая группе с l каналами, имеет среднюю величину:
 |
( 9.8) |
Мы принимаем, что потоки нагрузки независимы (не коррелированны), и таким образом дисперсия полного потока нагрузки будет равна:
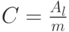 |
( 9.9) |
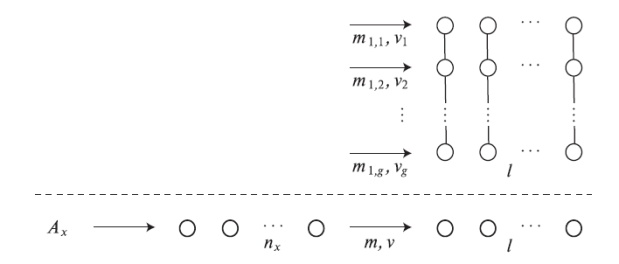
Рис. 9.5. Приложение ERТ-метода к системе, принимающей g независимых потоков нагрузки к общей группе l каналов. Объединенный процесс перегрузки g потоков нагрузки называют эквивалентной нагрузкой перегрузки от единственной полнодоступной группы с тем же самым математическим ожиданием и дисперсией нагрузки перегрузки (9.8) и (9.9)
Полная нагрузка характеризуется m и v. До сих пор мы принимали, что m < v. Теперь будем полагать, что эта нагрузка будет эквивалентна потоку нагрузки, который потерян от полнодоступной группы и имеет ту же самую среднюю величину т. и дисперсию v. На рис.9.5 верхняя часть системы заменена эквивалентной системой - нижней частью рис.9.5, которая является полнодоступной системой с 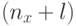 , каналами с предложенной нагрузкой
, каналами с предложенной нагрузкой 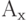 для данных значений т и v, поэтому решаем уравнения (9.6) и (9.7) относительно п и А. Можно показать, что существует уникальное решение, которое мы обозначим
для данных значений т и v, поэтому решаем уравнения (9.6) и (9.7) относительно п и А. Можно показать, что существует уникальное решение, которое мы обозначим 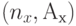 .
.
Потерянная нагрузка найдена по В-формуле Эрланга:
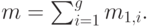 |
( 9.10) |
Предложенная нагрузка т перегрузки системы получается:
 |
( 9.11) |
Замечание: вероятность блокировки не равна 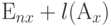 . Нужно помнить последний шаг (9.11), где мы связываем потерянную нагрузку с первоначально предложенной нагрузкой, которая в этом случае представлена т. (9.8).
. Нужно помнить последний шаг (9.11), где мы связываем потерянную нагрузку с первоначально предложенной нагрузкой, которая в этом случае представлена т. (9.8).
Заметим, что если нагрузка перегрузки от единственной первичной группы типа РСТ 1, тогда метод точен. В общем случае для большого числа потоков нагрузки метод приблизителен и не выдает точную среднюю вероятность блокировки.
Пример 9.2.1: Парадокс
В секции 6.3 мы получили теорему Пальма, в которой состояние рассматривается как суперпозиция многих процессов поступления независимых вызовов - мы получаем локальный Пуассоновский процесс. Это не противоречит (9.8) и (9.9), потому что эта формула справедлива глобально.
Числовые аспекты
При применении метода ERT мы должны вычислить (m, v) для данных значений (А, n) , и наоборот. Используя (9.4) и (9.5), можно просто получить (m, v) для данных (А, n) . Для того чтобы получить (А, n) для данных (m, v) , мы должны решить два уравнения с двумя неизвестными. Это требует применение итерационной процедуры, так как формула 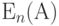 не может быть решена явно ни относительно n, ни относительно А (секция 7.5).
не может быть решена явно ни относительно n, ни относительно А (секция 7.5).
Однако мы можем решить (9.7) относительно n:
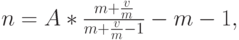 |
( 9.12) |
так, что мы можем знать n для данного А. Так что А - только одна независимая переменная. Мы можем использовать итеративный метод Ньютона-Рафсона, чтобы решить остающееся уравнение, вводя функцию:
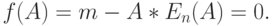
Задавая начальное значение 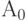 , мы многократно улучшаем это значение, пока не получаем конечное значения m и v/m, достаточно близкое к известным значениям.
, мы многократно улучшаем это значение, пока не получаем конечное значения m и v/m, достаточно близкое к известным значениям.
Ингве Рапп (Yngve Rapp 1965 [86]) предложил хорошее приблизительное решение А, которое может использоваться как начальное значение 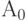 при итерации:
при итерации:
 |
( 9.13) |
Из А можно получить n, применяя (9.12). Приближение Рапа дает достаточно точные значения для практических приложений, кроме случаев, когда 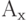 очень мало. Пиковость Z= v/m имеет максимум, который получается, когда п является немного большим, чем А (рис.9.4). Для некоторых комбинаций т и v/m конвергенция является критической, но при помощи компьютеров мы можем всегда найти правильное решение. В компьютерных вычислениях мы работаем с нецелым числом каналов и только в конце вычислений выбираем целое число каналов, большее или равное полученному результату (типичный модуль некоторого числа каналов 8 в GSM, 30 в ИКМ, и т.д.). При использовании таблиц по формуле В-Эрланга нужно на каждом шаге выбирать число каналов консервативным способом так, чтобы в худшем случае достигалась выбранная вероятность блокировки.
очень мало. Пиковость Z= v/m имеет максимум, который получается, когда п является немного большим, чем А (рис.9.4). Для некоторых комбинаций т и v/m конвергенция является критической, но при помощи компьютеров мы можем всегда найти правильное решение. В компьютерных вычислениях мы работаем с нецелым числом каналов и только в конце вычислений выбираем целое число каналов, большее или равное полученному результату (типичный модуль некоторого числа каналов 8 в GSM, 30 в ИКМ, и т.д.). При использовании таблиц по формуле В-Эрланга нужно на каждом шаге выбирать число каналов консервативным способом так, чтобы в худшем случае достигалась выбранная вероятность блокировки.
Вышеупомянутый метод предполагает, что v/m больше, чем единица. Это справедливо только для взрывной нагрузки.
Отдельный поток нагрузки на рис.9.5 позволяет иметь 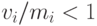 , если общее количество объединенных потоков нагрузки является взрывным. Брекшнайдер ( Bretschneider [9], 1973) расширил метод, включив в вычисления отрицательное число каналов. При этом способе есть шанс иметь дело со сглаженной нагрузкой ( EERT - Extended ERT method - Расширенный ERT-метод ).
, если общее количество объединенных потоков нагрузки является взрывным. Брекшнайдер ( Bretschneider [9], 1973) расширил метод, включив в вычисления отрицательное число каналов. При этом способе есть шанс иметь дело со сглаженной нагрузкой ( EERT - Extended ERT method - Расширенный ERT-метод ).
Вероятности блокировки пакета
Отдельные потоки нагрузки на рис. 9.5 не имеют одинаковой средней величины и дисперсии, и поэтому не дают равные вероятности блокировки в общей группе перегрузки с l каналами. Из рассмотренного выше мы вычисляем среднюю блокировку (9.11) для всех объединенных потоков нагрузки. Опыт показывает, что получаемая вероятность блокировки пропорциональна пиковости Z= v/m. Мы можем разбить полную потерянную нагрузку на отдельные пакеты потерянной нагрузки, принимая во внимание, что нагрузка, потерянная для потока i, пропорциональна  - средней величине и пиковости потока Z = v/m. Мы получаем:
- средней величине и пиковости потока Z = v/m. Мы получаем:
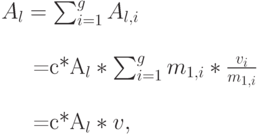
из этой формулы мы находим константу с = l/v.
Вероятность блокировки для нагрузки потока i, называемая вероятностью блокировки пакета для потока i, затем получается:
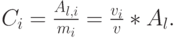 |
( 9.14) |
Кроме того, мы можем делить блокировку среди отдельных групп (первичная, вторичная, и т.д. группы). Рассмотрим эквивалентную группу внизу рис. 9.5 с 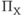 первичными каналами и l вторичными каналами (каналы перегрузки). Мы можем вычислить вероятность блокировки
первичными каналами и l вторичными каналами (каналы перегрузки). Мы можем вычислить вероятность блокировки 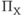 первичных каналов, и вероятности блокировки l вторичных каналов. Вероятность, что нагрузка потеряна l каналами, равна вероятности, что нагрузка потеряна
первичных каналов, и вероятности блокировки l вторичных каналов. Вероятность, что нагрузка потеряна l каналами, равна вероятности, что нагрузка потеряна 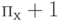 каналами, при условии, что потерянная нагрузка предлагается l каналам:
каналами, при условии, что потерянная нагрузка предлагается l каналам:
 |
( 9.15) |
Поэтому полная вероятность потерь связана с этими двумя группами:
 |
( 9.16) |
Используя это выражение, мы можем найти блокировку для каждой группы каналов и затем, например, получить информацию, какая группа должна быть увеличена добавлением большего числа каналов.
Пример 9.2.2: продолжение примера 9.1.1
В примере 9.1.1 вероятность блокировки первичной группы 8 каналов -  . Блокировка группы перегрузки:
. Блокировка группы перегрузки:
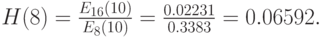
Полная блокировка системы:
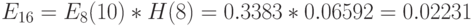
Пример 9.2.3: Иерархическая сотовая система
Мы рассматриваем иерархическую сотовую систему HCS (Hierarchical cellular system), имеющую три области покрытия. Нагрузка, предлагаемая в областях - 12, 8 и 4 Эрл. соответственно. В первых двух ячейках, мы размещаем микроячейки с 16-ью, соответственно с 8-ью каналами, и общую макроячейку, покрывающую все три области с 8-ью каналами. Перенаправляем потерянную нагрузку от микроячеек к макроячейке, но не направляем вызовы от макроячейки к микроячейкам, когда канал освобождается. Не будем рассматривать здесь нагрузку передачи соединения. Используя (9.6) и (9.7), находим среднюю величину и дисперсию нагрузки, предлагаемую макроячейке:
| Номер ячейки | Предложенная нагрузка | Число каналов | Средняя перегрузка | Дисперсия перегрузки | Пиковость |
|---|---|---|---|---|---|
 |
 |
 |
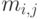 |
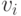 |
 |
| 1 | 12 | 16 | 0,7250 | 1,7190 | 2,3711 |
| 2 | 8 | 8 | 1,8846 | 3,5596 | 1,888 |
| 3 | 4 | 0 | 4,000 | 4,000 | 1,000 |
| Всего | 24 | 6,6095 | 9,2786 | 1,4038 |
Полная нагрузка, предлагаемая макроячейке, имеет среднюю величину 6,61 Эрл. и дисперсию 9,28. Это соответствует перегрузке от эквивалентной системы с 10,78 Эрл; здесь требуется 4,72 каналов. Таким образом, мы выбираем систему 12,72 каналов, с предложенной нагрузкой 10,78 Эрл. Используя В-формулу Эрланга, находим потерянную нагрузку 1,3049 Эрл. Первоначально мы предложили значение 24 Эрл., так что полная вероятность блокировки нагрузки получается В = 5,437 %.
Эти три области имеют отдельные вероятности блокировки. Применив (9.14), мы приблизительно находим потерянную нагрузку от областей: 0,2434 Эрл, 0,5042 Эрл, и 0,5664 Эрл, соответственно. Таким образом, вероятности блокировки нагрузки становятся 2,03 %, 6,30 % и 14,16 %, соответственно. Компьютерное моделирование со 100 миллионами вызовов выдает вероятности блокировки 1,77 %, 5,2 %, и 15,05 %, соответственно. Это соответствует полной потерянной нагрузке, равной 1,273 Эрл, и вероятности блокировки 5.30 %. Точность метода этой лекции достаточна для реальных приложений.
Метод Фредерикса и Хэйварда
Фредерике (1980 [29]) предложил метод эквивалентности, который более прост в использовании, чем метод Брейтшнайдера-Уилкинсона (Wilkinson-Bretschneider). Идея метода была впервые выдвинута Хэйвардом.
Метод эквивалентности Фредерикса и Хэйварда также характеризует нагрузку средней величиной А и пиковостью Z
( 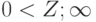 )( Z = 0 - тривиальный случай с постоянной нагрузкой). Пиковость (7.7) - отношение между дисперсией v и средней величиной
)( Z = 0 - тривиальный случай с постоянной нагрузкой). Пиковость (7.7) - отношение между дисперсией v и средней величиной 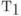 вероятностей состояния, она имеет размерность [каналы]. Для случайной нагрузки ( PCT-II ) мы примем Z=l и можем применить В-формулу Эрланга.
вероятностей состояния, она имеет размерность [каналы]. Для случайной нагрузки ( PCT-II ) мы примем Z=l и можем применить В-формулу Эрланга.
Для пиковости 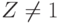 метод Фредерикса и Хэйварда предполагает, что система имеет ту же самую вероятность блокировки, что и система из n/Z каналами с предложенной нагрузкой A/Z, и таким образом пиковость Z=l. Для последней системы мы можем применить В-формулу Эрланга, при этом следует учитывать, что В-формулу Эрланга нельзя использовать для непрерывного числа каналов.
метод Фредерикса и Хэйварда предполагает, что система имеет ту же самую вероятность блокировки, что и система из n/Z каналами с предложенной нагрузкой A/Z, и таким образом пиковость Z=l. Для последней системы мы можем применить В-формулу Эрланга, при этом следует учитывать, что В-формулу Эрланга нельзя использовать для непрерывного числа каналов.
Башарин и Куренков расширили метод, включив мультислотовую (мультискоростную) нагрузку, где вызов требует d каналов от начала и до завершения. Если вызов использует d каналов вместо одного (изменение масштаба), то средняя величина времени становится в d раз больше, и дисперсия времени больше в 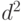 раз. Поэтому пиковость по времени становится больше в d раз. Вместо того, чтобы сократить число каналов на число Z, мы можем оставить прежнее число каналов и увеличить размер слота на Z
раз. Поэтому пиковость по времени становится больше в d раз. Вместо того, чтобы сократить число каналов на число Z, мы можем оставить прежнее число каналов и увеличить размер слота на Z
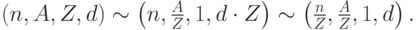 |
( 9.18) |
Если мы имеем больше потоков нагрузки, предлагаемых той же самой группе, то хорошей стратегией будет сохранить число каналов фиксированным, но тогда мы получаем проблему, что 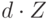 B общем случае не будут целыми числами.
B общем случае не будут целыми числами.
Пример 9.3.1: Метод Фредерикса и Хэйварда
Применим метод ФредериксаиХэйварда кпримеру 9.2.3. Макроячейка будет иметь (8/1,4038) каналов и предложенную нагрузку (6,6095/1,4038) Эрл. Вероятность блокировки получена из В-формулы Эрланга и равна 0,19470. Потерянная нагрузка вычислена из первоначально предложенной нагрузки (6,6095) и равна 1,2871 Эрл. Вероятность блокировки системы становится Е= 1,2871/24 = 5.36 %. Это очень близко к результату, который мы получили (5.44 %) методом ERT.
Пример 9.3.2: Мультислотовый трафик
Мы позже рассмотрим систему с интегрированным обслуживанием и мультискоростной (мультислотовой) нагрузкой. В примере 10.4.3 рассматривалась группа с пучком 1536 каналов, которой предлагается 24 потока нагрузки с индивидуальным размером слота и пиковостью. Полные потери по нагрузке равны 5,950 %. Если мы вычисляем пиковость из предложенной нагрузки, складывая все потоки нагрузки, то находим пиковость Z= 9,8125, а полная средняя величина равняется 1536 Эрл. Результаты метода Фредерикса и Хэйварда для полной нагрузке перегрузки равняются 6,114 %, что является консервативной оценкой (худший случай).