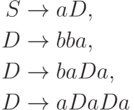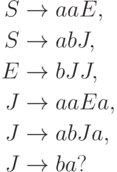|
Упражнение 2.1.25 |
Слова, языки и грамматики
1.4. Порождающие грамматики
Определение 1.4.1. Порождающей грамматикой
( грамматикой типа 0,
generative grammar, rewrite grammar)
называется четверка 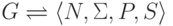 ,
где N и
,
где N и  - конечные алфавиты,
- конечные алфавиты, 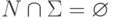 ,
, 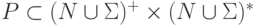 , P конечно и
, P конечно и 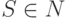 .
Здесь
.
Здесь  - основной алфавит
( терминальный алфавит ),
его элементы называются терминальными символами
или терминалами (terminal), N - вспомогательный алфавит
( нетерминальный алфавит ),
его элементы называются нетерминальными символами,
нетерминалами,
вспомогательными символами или переменными
(nonterminal, variable), S - начальный символ
( аксиома,
start symbol).
Пары
- основной алфавит
( терминальный алфавит ),
его элементы называются терминальными символами
или терминалами (terminal), N - вспомогательный алфавит
( нетерминальный алфавит ),
его элементы называются нетерминальными символами,
нетерминалами,
вспомогательными символами или переменными
(nonterminal, variable), S - начальный символ
( аксиома,
start symbol).
Пары  называются правилами подстановки,
просто правилами или продукциями
(rewriting rule, production)
и записываются в виде
называются правилами подстановки,
просто правилами или продукциями
(rewriting rule, production)
и записываются в виде  .
.
Пример 1.4.2.
Пусть даны множества N = {S}, 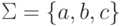 ,
,  .
Тогда
.
Тогда 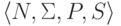 является порождающей грамматикой.
является порождающей грамматикой.
Замечание 1.4.3.
Будем обозначать
элементы множества  строчными буквами из начала латинского алфавита,
а элементы множества N -
заглавными латинскими буквами.
Обычно в примерах мы будем задавать грамматику в виде списка правил,
подразумевая, что алфавит N
составляют все заглавные буквы, встречающиеся в правилах,
а алфавит
строчными буквами из начала латинского алфавита,
а элементы множества N -
заглавными латинскими буквами.
Обычно в примерах мы будем задавать грамматику в виде списка правил,
подразумевая, что алфавит N
составляют все заглавные буквы, встречающиеся в правилах,
а алфавит  -
все строчные буквы, встречающиеся в правилах.
При этом правила порождающей грамматики записывают в таком порядке,
что левая часть первого правила
есть начальный символ S.
-
все строчные буквы, встречающиеся в правилах.
При этом правила порождающей грамматики записывают в таком порядке,
что левая часть первого правила
есть начальный символ S.
Замечание 1.4.4.
Для обозначения n правил с одинаковыми левыми частями 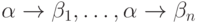 часто используют сокращенную запись
часто используют сокращенную запись  .
.
Определение 1.4.5.
Пусть дана грамматика G.
Пишем 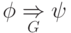 ,
если
,
если  ,
, 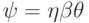 и
и 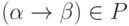 для некоторых слов
для некоторых слов 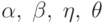 в алфавите
в алфавите  .
Если
.
Если  ,
то говорят, что
слово
,
то говорят, что
слово  непосредственно выводимо
из слова
непосредственно выводимо
из слова  .
.
Замечание 1.4.6.
Когда из контекста ясно, о какой
грамматике идет речь,
вместо  можно писать просто
можно писать просто  .
.
Пример 1.4.7. Пусть
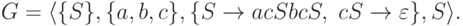
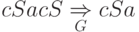 .
.Определение 1.4.8. Если  ,
где
,
где 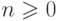 ,
то пишем
,
то пишем  и говорим, что
слово
и говорим, что
слово 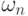 выводимо
из слова
выводимо
из слова 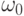 .
Другими словами, бинарное отношение
.
Другими словами, бинарное отношение 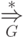 является рефлексивным, транзитивным замыканием
бинарного отношения
является рефлексивным, транзитивным замыканием
бинарного отношения 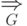 ,
определенного на множестве
,
определенного на множестве 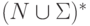 .
.
При этом последовательность слов 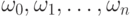 называется выводом (derivation)
слова
называется выводом (derivation)
слова 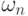 из слова
из слова 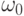 в грамматике G.
Число n
называется длиной
( количеством шагов )
этого вывода.
в грамматике G.
Число n
называется длиной
( количеством шагов )
этого вывода.
Замечание 1.4.9.
В частности, для всякого слова 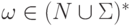 имеет место
имеет место  (так как возможен вывод длины 0 ).
(так как возможен вывод длины 0 ).
Пример 1.4.10.
Пусть  .
Тогда
.
Тогда 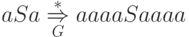 .
Длина этого вывода - 3.
.
Длина этого вывода - 3.
Определение 1.4.11. Язык, порождаемый
грамматикой G, - это множество  .
Будем также говорить, что грамматика G порождает (generates) язык L(G).
.
Будем также говорить, что грамматика G порождает (generates) язык L(G).
Замечание 1.4.12.
Существенно, что в определение порождающей грамматики
включены два алфавита -  и N.
Это позволило нам в определении 1.4.11 "отсеять" часть слов, получаемых из начального символа.
А именно, отбрасывается каждое слово, содержащее хотя бы один символ,
не принадлежащий алфавиту
и N.
Это позволило нам в определении 1.4.11 "отсеять" часть слов, получаемых из начального символа.
А именно, отбрасывается каждое слово, содержащее хотя бы один символ,
не принадлежащий алфавиту  .
.
Пример 1.4.13.
Если  ,
то
,
то 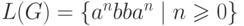 .
.
Определение 1.4.14. Две грамматики эквивалентны, если они порождают один и тот же язык.
Пример 1.4.15. Грамматика
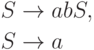
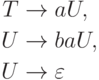
Упражнение 1.4.16. Описать язык, порождаемый грамматикой
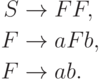
Упражнение 1.4.17. Описать язык, порождаемый грамматикой
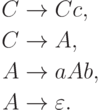
Упражнение 1.4.18. Описать язык, порождаемый грамматикой
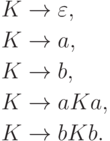
Упражнение 1.4.19. Описать язык, порождаемый грамматикой
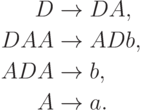
Упражнение 1.4.20. Описать язык, порождаемый грамматикой

Упражнение 1.4.21. Описать язык, порождаемый грамматикой
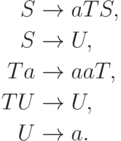
Упражнение 1.4.22. Эквивалентны ли грамматика
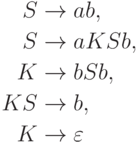
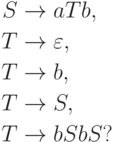
Упражнение 1.4.23. Эквивалентны ли грамматика