НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 13: Квантовый аналог NP: класс BQNP

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 613 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

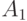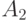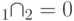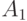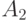Лемма 13.4. Пусть A_1 , A_2 — неотрицательные операторы, $\calL_1$ , $\calL_2$ — их нулевые подпространства, причем $\calL_1\cap \calL_2=0$ . Пусть также ненулевые собственные числа A_1 и A_2 не меньше 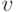. Тогда

$\begin{equation} A_1+A_2\geq v\cdot 2\sin^2\frac{\vt}{2}, \end{equation}$

( 13.16)

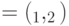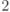где $\vt=\vt(\calL_1,\calL_2)$ — угол между $\calL_1$ и $\calL_2$ .

Обозначение $A\geq a$ ( — оператор, — число) нужно понимать как сокращение от $A-aI\geq0$ . Другими словами, если $A\geq a$ , то все собственные числа не меньше .

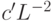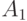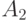В нашем случае мы получим оценки и $c'L^{-2}$ для ненулевых собственных чисел A_1 и A_2 (об этом уже говорилось выше) и $\sin^2\vt\double\geq (1-\sqrt{\eps})/(L+1)$ для угла. Отсюда вытекает искомое неравенство

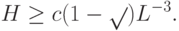
$H\double\geq c(1-\sqrt{\eps})L^{-3}.$

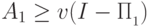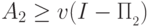Доказательство (леммы 13.4). Очевидно, что $A_1\ge v(I-\Pi_{\calL_1})$ и $A_2\ge v(I-\Pi_{\calL_2})$ , поэтому достаточно доказать неравенство 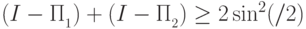$(I-\Pi_{\calL_1})\double+(I-\Pi_{\calL_2})\ge 2\sin^2(\vt/2)$ . Оно, в свою очередь, эквивалентно такому неравенству:

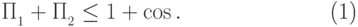$\begin{equation}\label{сумма-проекторов} \Pi_{\calL_1}+\Pi_{\calL_2}\le 1+\cos\vt. \end{equation}$

( 13.17)

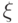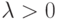Пусть $\ket\xi$ — собственный вектор оператора $\Pi_{\calL_1}+\Pi_{\calL_2}$ , отвечающий собственному числу $\lambda>0$ . Тогда

$\Pi_{\calL_1}\ket\xi=u_1\ket{\eta_1},\quad\ \Pi_{\calL_2}\ket\xi=u_2\ket{\eta_2},\qquad u_1\ket{\eta_1}+u_2\ket{\eta_2}=\lambda\ket\xi,$

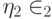где $\ket{\eta_1}\in\calL_1$ и $\ket{\eta_2}\in\calL_2$ — единичные векторы, а u_1

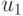и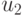

— неотрицательные вещественные числа. Отсюда находим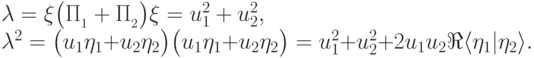

$\begin{multiline} \lambda=\bra\xi\bigl(\Pi_{\calL_1}+\Pi_{\calL_2}\bigr)\ket\xi=u_1^2+u_2^2,\\ \lambda^2=\bigl(u_1\bra{\eta_1}+u_2\bra{\eta_2}\bigr) \bigl(u_1\ket{\eta_1}+u_2\ket{\eta_2}\bigr)= u_1^2+u_2^2+2u_1u_2\Re\langle\eta_1|\eta_2\rangle. \end{multiline}$

Следовательно,

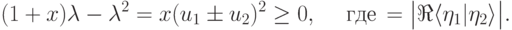
$(1+x)\lambda-\lambda^2=x(u_1\pm u_2)^2\ge 0,\quad\ \text{где}\,\x=\bigl|\Re\langle\eta_1|\eta_2\rangle\bigr|.$

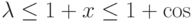Таким образом, $\lambda\le 1+x\le 1+\cos\vt$ .

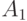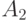Теперь получим упомянутые выше оценки. Нулевые подпространства A_1 и A_2 представляются в виде

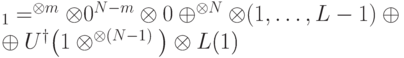$\begin{equation} \calL_1=\BB^{\otimes m}\otimes\ket{0^{N-m}}\otimes\ket{0} &\oplus \BB^{\otimes N}\otimes\CC(\ket1,\dots,\ket{L-1}) \oplus\\ &\oplus U^\dagger\big(\ket1\otimes\BB^{\otimes(N-1)}\big)\otimes\ket{L} \label{L1} \end{equation}$

( 13.18)

(последний сомножитель во всех слагаемых относится к пространству счетчика),

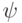$\begin{equation} \calL_2=\BB^{\otimes N}\otimes\ket\psi, \label{L2} \end{equation}$

( 13.19)

где вектор $\ket\psi$ определен формулой (13.14).

Для оценки

$\begin{equation}\label{A1} A_1\restrict{}_{\calL_1^\bot} \geq1 \end{equation}$

( 13.20)

достаточно заметить, что A_1

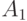является суммой коммутирующих друг с другом проекторов, поэтому все собственные числа этого оператора целые.

Для оценки 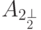$\mkern2mu A_2\restrict{}_{\calL_2^\bot}$ нужно найти первое положительное собственное число матрицы 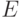. Собственные векторы и собственные числа даются формулами

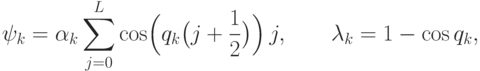
$\ket{\psi_k}=\alpha_k\sum_{j=0}^{L} \cos\Bigl(q_k\bigl(j+\frac{1}{2}\bigr)\Bigr)\,\ket{j},\qquad \lambda_k=1-\cos q_k,$

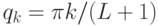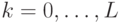где $q_k=\pi k/(L+1)$ \, ( $k=0,\dots,L$ ). Отсюда следует, что

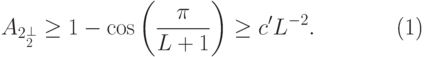$\begin{equation}\label{A2} A_2\restrict{}_{\calL_2^\bot}\ge 1-\cos\left(\frac{\pi}{L+1}\right) \ge c'L^{-2}. \end{equation}$

( 13.21)

Наконец, нужно оценить угол между подпространствами $\calL_1$ и $\calL_2$ . Будем оценивать квадрат косинуса угла

$\begin{equation}\label{косинус-оценка} \cos^2\vt= \max\limits_{\begin{array}{l} \scriptstyle\ket{\eta_1}\in \calL_1\\[-2pt] \scriptstyle\ket{\eta_2}\in \calL_2\end{array}}\mkern-4mu \big|\langle \eta_1\ket{\eta_2}\big|^2= \max\limits_{\scriptstyle\ket{\eta_2}\in \calL_2} \langle \eta_2|\Pi_{\calL_1}|\eta_2\rangle. \end{equation}$

( 13.22)

Представим $\ket{\eta_2}$ в виде $\ket\xi\otimes\ket\psi$ . Проектор на $\calL_1$ распадается на сумму трех проекторов, в соответствии с (13.18). Совсем легко подсчитать вклад второго слагаемого, он равен (L-1)/(L+1)

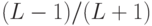. Первое и третье слагаемые в сумме дают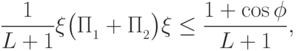

$\frac{1}{L+1}\bra\xi\bigl(\Pi_{\calK_1}+\Pi_{\calK_2}\bigr)\ket\xi \le \frac{1+\cos\phi}{L+1},$

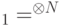где $\calK_1=\BB^{\otimes N}$ , $\calK_2=U^\dagger\left(\ket{1}\otimes\BB^{\otimes(N-1)}\right)$ , а $\phi$ — угол между этими двумя подпространствами. (Здесь используется неравенство(13.17), полученное в ходе доказательства леммы 13.4).

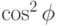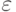Величина $\cos^2\phi$ равна максимальной вероятности получения ответа исходной схемой; по условию она не больше, чем $\eps$ . Получаем такую, продолжающую (13.22), оценку:

$\langle \eta_2|\Pi_{\calL_1}|\eta_2\rangle \le \frac{L-1}{L+1}+\frac{1+\sqrt{\eps}}{L+1} = 1-\frac{1-\sqrt{\eps}}{L+1}.$

Следовательно, $\sin^2\vt=1-\cos^2\vt\ge(1-\sqrt{\eps})/(L+1)$ , как и утверждалось выше.

Реализация счетчика. Мы написали замечательный гамильтониан, почти удовлетворяющий требуемым свойствам. У него есть только один недостаток — он лишь 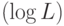$(\log L)$ -локальный (в пространстве счетчика мы действуем на все q-биты).

Этот недостаток можно преодолеть, если вложить пространство счетчика в большее пространство. Возьмем 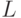q-битов, занумерованных от до 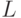. Искомое вложение 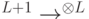$\CC^{L+1}\to\BB^{\otimes L}$ выглядит так:

$\ket{j} \mapsto \ket{% \underbrace{1,\dots, 1}_{\scriptstyle j}, \underbrace{0,\dots, 0}_{\scriptstyle L-j}}.$

Используемые в конструкции гамильтониана

операторы на пространстве счетчика заменяются согласно схеме

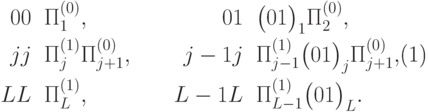$\begin{equation}\label{extend} \begin{aligned} \ket{0}\bra{0} &\mathrel{\mathrm{ на }} \Pi^{(0)}_{1}, & \quad&& \ket{0}\bra{1} &\mathrel{\mathrm{ на }} \bigl(\ket0\bra1\bigr)_{1}\Pi^{(0)}_{2},\\ \ket{j}\bra{j} &\mathrel{\mathrm{ на }} \Pi^{(1)}_{j} \Pi^{(0)}_{j+1}, &\quad&& \ket{j-1}\bra{j} &\mathrel{\mathrm{ на }} \Pi^{(1)}_{j-1}\bigl(\ket0\bra1\bigr)_{j} \Pi^{(0)}_{j+1}, \\ \ket{L}\bra{L} &\mathrel{\mathrm{ на }} \Pi^{(1)}_{L}, &\quad&& \ket{L-1}\bra{L} &\mathrel{\mathrm{ на }}\Pi^{(1)}_{L-1}\bigl(\ket0\bra1\bigr)_{L}. \end{aligned} \end{equation}$

( 13.23)

Теперь они 3-локальные (а сам гамильтониан, с учетом действия на q-биты исходной схемы, — 5-локальный).

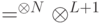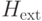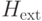Если говорить точнее, мы заменили гамильтониан , действовавший на пространстве $\calL=\BB^{\otimes N}\otimes\CC^{L+1}$ , на новый гамильтониан $H_{\rm ext}$ , определенный на большем пространстве $\calL_{\rm ext}=\BB^{\otimes N}\otimes\BB^{\otimes L}$ . Оператор $H_{\rm ext}$ отображает подпространство 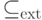$\calL\subseteq\cal\calL_{\rm ext}$ в себя и действует на нем так же, как .

Теперь возникает новая проблема: что делать с лишними состояниями в расширенном пространстве счетчика? Мы справимся с этой проблемой, добавив еще одно слагаемое к гамильтониану 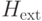$H_{\rm ext}$ :

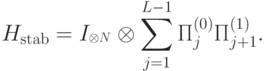
$H_{\rm stab}=I_{\BB^{\otimes N}}\otimes \sum_{j=1}^{L-1} \Pi^{(0)}_j \Pi^{(1)}_{j+1}.$

Нулевое подпространство оператора 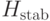$H_{\rm stab}$ совпадает со старым рабочим пространством $\calL$ , поэтому дополнительное слагаемое не меняет верхней оценки минимального собственного числа при ответе "да".

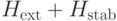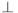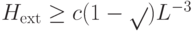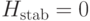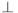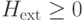При ответе "нет" требуемую нижнюю оценку для собственных чисел оператора $H_{\rm ext}+H_{\rm stab}$ можно получить следующим образом. Оба слагаемых оставляют инвариантным подпространство $\calL$ , поэтому можно оценивать независимо на $\calL$ и его ортогональном дополнении $\calL^\perp$ . 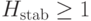На $\calL$ имеем $H_{\rm ext}\ge c(1-\sqrt{\eps})L^{-3}$ и $H_{\rm stab}=0$ , а на $\calL^\perp$ — $H_{\rm ext}\ge 0$ и $H_{\rm stab}\ge 1$ . (Здесь мы пользуемся тем, что каждое из слагаемых гамильтониана, (13.8), (13.9) и (13.10), остается неотрицательным при замене (13.23)). В любом случае

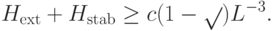
$H_{\rm ext}+H_{\rm stab}\double\geq c(1-\sqrt{\eps})L^{-3}.$

Это завершает доказательство полноты задачи о локальном гамильтониане в классе BQNP.

Место BQNP среди других сложностных классов.

Прямо из определения следует, что класс BQNP содержит класс MA (а, значит, и BPP, и NP). Ничего более определенного о силе "недетерминированных" квантовых алгоритмов сказать пока нельзя^{1Предупреждение: в литературе встречается другое определение квантового недетерминированного вычисления, для которого получена полная характеризация в терминах классических сложностных классов (см. [46]).}

Не слишком много можно сказать и об их "слабости".

Утверждение 13.5. 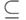$\BQNP\subseteq\PSPACE$ .

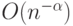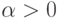Доказательство. Максимальная вероятность того, что подсказка Мерлина будет принята Артуром, равна масимальному собственному числу оператора $X=X^{(1)}$ (см. формулу (13.3)). Нам нужно вычислить эту величину с точностью $O(n^{-\alpha})$ , ( $\alpha>0$ ).

Заметим, что 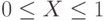$0\le X\le 1$ . Для оценки максимального собственного числа будем использовать следующее предельное равенство:

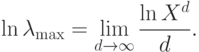
$\ln\lambda_{\rm max}=\lim_{d\to\infty}\frac{\ln \Tr X^d}{d}.$

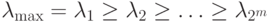Пусть $\lambda_{\rm max}=\lambda_1\ge\lambda_2\ge\ldots\ge\lambda_{2^m}$ — собственные числа оператора

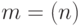(здесь $m=\poly(n)$ — длина подсказки). Имеем оценку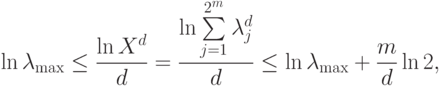

$\ln\lambda_{\rm max}\leq\frac{\ln \Tr X^d}{d}=\frac{\ln\sum\limits_{j=1}^{2^m}\lambda_j^d}{d} \leq \ln\lambda_{\rm max}+\frac{m}{d}\ln 2,$

из которой следует, что для оценки с полиномиальной точностью неотрицательного оператора, действующего на

q-битах, достаточно вычислить след от его степени, ограниченной полиномом от

.

Вычисление величины 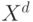$\Tr X^d$ делается на полиномиальной памяти тем же способом, что и моделирование работы квантовой схемы.

Замечание 13.3. Полученный результат можно усилить: 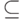$\BQNP\double\subseteq\PPP$ . Доказательство полностью аналогично решению задачи 8.3.

Замечание 13.4. Мы ограничились случаем игр Мерлина и Артура, которые продолжаются один раунд. Недавно было показано [45], что уже двух раундов такой квантовой игры достаточно, чтобы получить весь класс PSPACE. В классическом случае для достижения класса PSPACE требуется полиномиальное количество раундов [36, 37], причем в широких кругах узких специалистов господствует мнение, что никакого фиксированного количества раундов недостаточно.

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Квантовый аналог NP: класс BQNP

Место BQNP среди других сложностных классов.

Вопросы и ответы