Физически реализуемые преобразования матриц плотности
Подсчет вероятностей для квантового вычисления.
Теперь, имея общие определения квантовой вероятности и физически реализуемого преобразования матриц плотности, можно вычислять вероятности, входящие в определение квантового вычисления, двумя способами. Пусть мы использовали при вычислениях дополнительную подсистему. После того, как она стала нам не нужна, мы можем выбросить ее в мусорную корзину, а при подсчете вероятности взять частичный след по пространству состояний дополнительной подсистемы. А можно тянуть весь этот мусор до самого конца и считать вероятность для событий вида  (раз уж мы перестали использовать вторую подсистему, то никакие детали ее состояния нам не важны — нам безразлично, что именно произойдет с использованной подсистемой в мусорной корзине). Как уже говорилось, эти вероятности равны:
(раз уж мы перестали использовать вторую подсистему, то никакие детали ее состояния нам не важны — нам безразлично, что именно произойдет с использованной подсистемой в мусорной корзине). Как уже говорилось, эти вероятности равны: 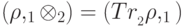 .
.
Замечание. Нетрудно определить более общую модель квантового вычисления, в которой элементарными действиями являются подходящие преобразования матриц плотности общего вида (не обязательно унитарные операторы). Такая модель более адекватна физической ситуации, когда квантовый компьютер взаимодействует с "окружающей средой". С вычислительной точки зрения новая модель эквивалентна стандартной (если в обоих случаях используется полный базис). Однако в модели с общими преобразованиями матриц плотности возможно более естественное определение подпрограммы для квантового вычисления, поскольку результат работы квантовой схемы — вероятностная функция. Здесь мы не будем давать этого определения и отсылаем заинтересованного читателя к [20].
Потеря когерентности (decoherence).
Рассмотрим в качестве примера преобразование матриц плотности, которое "забывает" внедиагональные элементы:
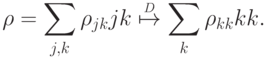
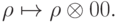
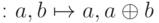 . Получаем
. Получаем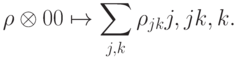
А теперь возьмем частичный след по добавленным битам. Получим диагональную матрицу
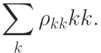
Предостережение. Рассмотренная нами "операция копирования"
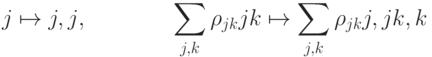
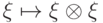 является нелинейным оператором, поэтому не может быть реализовано физически. В дальнейшем копирование всегда будет определяться относительно некоторого базиса.
является нелинейным оператором, поэтому не может быть реализовано физически. В дальнейшем копирование всегда будет определяться относительно некоторого базиса.Замечание 10.2. Рассмотренное преобразование переводит любое состояние в классическое (с диагональной матрицей плотности), используя копирование битов. Это можно интерпретировать так: если постоянно наблюдать за системой (делать копии), то система будет вести себя как классическая. В случае одного q-бита то же самое преобразование (обнуление внедиагональных элементов) можно получить, если применить оператор 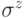 с вероятностью
с вероятностью 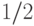 :
:
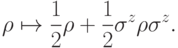
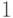 домножается на фазовый множитель
домножается на фазовый множитель  с вероятностью
с вероятностью  . Таким образом, сбой фазы также приводит к тому, что система ведет себя как классическая.
. Таким образом, сбой фазы также приводит к тому, что система ведет себя как классическая.Задача 10.5. Пусть имеется физически реализуемое преобразование 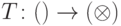 со следующим свойством:
со следующим свойством: 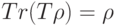 для любого чистого состояния
для любого чистого состояния  . Докажите, что тогда
. Докажите, что тогда  (для любого оператора
(для любого оператора  ), где
), где  — некоторая фиксированная матрица плотности на пространстве
— некоторая фиксированная матрица плотности на пространстве  .
.
Таким образом, нельзя получить никакой информации о неизвестном состоянии  , не возмущая это состояние.
, не возмущая это состояние.
