Иерархия сложностных классов
Класс PSPACE.
Как уже говорилось, в этот класс попадают те функции, которые могут быть вычислены на МТ, использующей память, ограниченную полиномом от длины входного слова. Класс PSPACE также можно описать, используя игры.
Теорема 4.2. 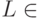 тогда и только тогда, когда существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что
тогда и только тогда, когда существует такая игра с полиномиальным от длины входного слова числом ходов и полиномиально вычислимым результатом, что 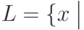 Б имеет выигрышную стратегию
Б имеет выигрышную стратегию 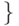 .
.
Доказательство  Покажем, что язык, определяемый игрой, принадлежит
Покажем, что язык, определяемый игрой, принадлежит  . Пусть число ходов ограничено
. Пусть число ходов ограничено 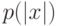 . Определим по индукции набор машин Тьюринга
. Определим по индукции набор машин Тьюринга 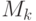 для
для 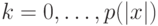 . Каждая
. Каждая 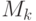 по заданному началу игры
по заданному началу игры 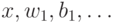 длины
длины  определяет наличие выигрышной стратегии у Б. Последней в этом ряду машине
определяет наличие выигрышной стратегии у Б. Последней в этом ряду машине  нужно просто вычислить предикат
нужно просто вычислить предикат 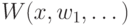 . Машина
. Машина 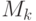 перебирает все возможные варианты
перебирает все возможные варианты 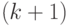 -го хода и консультируется с
-го хода и консультируется с 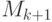 по поводу окончательных результатов игры. Ее оценка игры составляется очень просто: если текущий ход у Б, то достаточно найти один ход, при котором
по поводу окончательных результатов игры. Ее оценка игры составляется очень просто: если текущий ход у Б, то достаточно найти один ход, при котором 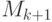 гарантирует выигрышную стратегию для Б. Если текущий ход у Ч, то при всех вариантах
гарантирует выигрышную стратегию для Б. Если текущий ход у Ч, то при всех вариантах 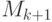 должна обнаружить выигрышную стратегию для Б. Машина
должна обнаружить выигрышную стратегию для Б. Машина 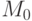 определяет наличие выигрышной стратегии для Б в самом начале игры и для ее работы нам нужно использовать всю последовательность машин
определяет наличие выигрышной стратегии для Б в самом начале игры и для ее работы нам нужно использовать всю последовательность машин 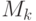 . Но каждая из этих машин использует небольшую (полиномиально ограниченную) память, так что весь процесс потребует лишь полиномиально ограниченной памяти.
. Но каждая из этих машин использует небольшую (полиномиально ограниченную) память, так что весь процесс потребует лишь полиномиально ограниченной памяти.
 Пусть есть машина
Пусть есть машина  , распознающая вхождение слова в язык
, распознающая вхождение слова в язык  на полиномиальной памяти. Во-первых, заметим, что вычисление на памяти
на полиномиальной памяти. Во-первых, заметим, что вычисление на памяти  бессмысленно проводить дольше, чем время
бессмысленно проводить дольше, чем время 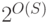 (все начнет повторяться после того, как мы исчерпаем все состояния нашей системы, а их не более чем
(все начнет повторяться после того, как мы исчерпаем все состояния нашей системы, а их не более чем  , где
, где  — соответственно множество состояний управляющего устройства и алфавит рассматриваемой МТ). Поэтому можно считать без ограничения общности, что время работы машины
— соответственно множество состояний управляющего устройства и алфавит рассматриваемой МТ). Поэтому можно считать без ограничения общности, что время работы машины  ограничено
ограничено 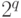 , где
, где  .
.
Чтобы было проще описывать игру, потребуем, чтобы после завершения вычисления МТ сохраняла без изменений достигнутое состояние.
Игра заключается в следующем. Белые утверждают, что ответ на входном слове  равен "да", а черные хотят это проверить. Белые своим первым ходом декларируют состояние машины
равен "да", а черные хотят это проверить. Белые своим первым ходом декларируют состояние машины  (строка, записанная на ленте, положение читающей головки, состояние управляющего устройства) после
(строка, записанная на ленте, положение читающей головки, состояние управляющего устройства) после 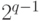 тактов. Черные своим ходом выбирают один из промежутков: от начала до
тактов. Черные своим ходом выбирают один из промежутков: от начала до 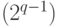 -го такта или от
-го такта или от 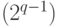 -го такта до конца. Белые декларируют состояние
-го такта до конца. Белые декларируют состояние  в середине этого промежутка. Далее все повторяется: Ч выбирает одну из половинок, Б декларирует состояние
в середине этого промежутка. Далее все повторяется: Ч выбирает одну из половинок, Б декларирует состояние  в середине выбранной половинки и т.д.
в середине выбранной половинки и т.д.
Игра заканчивается, когда длина промежутка становится равной 1. Результат определяется так: для обоих концов этого промежутка в процессе игры были названы состояния  . Если состояние правого конца получается из состояния левого конца за один такт работы
. Если состояние правого конца получается из состояния левого конца за один такт работы  , то Б выиграли, иначе выиграли Ч.
, то Б выиграли, иначе выиграли Ч.
Если ответ  на слове
на слове  действительно "да", то белым нужно все время говорить правду, это гарантирует им выигрыш.
действительно "да", то белым нужно все время говорить правду, это гарантирует им выигрыш.
Если ответ  на слове
на слове  — "нет", то при любом ходе белых на одном из промежутков (или на обоих) будет содержаться ошибка. Ч должен указывать каждый раз именно этот промежуток.
— "нет", то при любом ходе белых на одном из промежутков (или на обоих) будет содержаться ошибка. Ч должен указывать каждый раз именно этот промежуток.
Задача 4.1. Докажите, что класс языков, распознаваемых недетерминированными машинами, работающими на памяти  , содержится в классе языков, распознаваемых детерминированными машинами, работающими на памяти
, содержится в классе языков, распознаваемых детерминированными машинами, работающими на памяти  .
.
В качестве следствия теоремы 4.2 получаем включения всех определенных выше классов 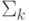 ,
, 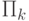 в класс
в класс  . Взаимное соотношение этих классов можно изобразить диаграммой включений, показанной ниже. На этой диаграмме от большего класса к меньшему можно пройти, двигаясь по стрелкам. Внизу располагается класс
. Взаимное соотношение этих классов можно изобразить диаграммой включений, показанной ниже. На этой диаграмме от большего класса к меньшему можно пройти, двигаясь по стрелкам. Внизу располагается класс 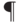 , отвечающий играм с 0 ходов, затем идут дополняющие друг друга классы, отвечающие играм с конечным числом ходов (для одного хода это NP и co-NP, для двух ходов —
, отвечающий играм с 0 ходов, затем идут дополняющие друг друга классы, отвечающие играм с конечным числом ходов (для одного хода это NP и co-NP, для двух ходов —  и
и 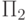 и т.д.). Завершается эта диаграмма классом
и т.д.). Завершается эта диаграмма классом  , который определяется произвольными играми с одним естественным условием — время игры должно быть полиномиально ограничено размером входного слова. Мы уже доказали все включения, изображенные на этой диаграмме. Ни про одно из включений, следующих из этой диаграммы, неизвестно, является ли оно строгим. Быть может, скажем,
, который определяется произвольными играми с одним естественным условием — время игры должно быть полиномиально ограничено размером входного слова. Мы уже доказали все включения, изображенные на этой диаграмме. Ни про одно из включений, следующих из этой диаграммы, неизвестно, является ли оно строгим. Быть может, скажем,  . С другой стороны, возможно и так, что
. С другой стороны, возможно и так, что 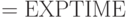 , где
, где 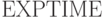 обозначает (не рассматривавшийся нами) класс языков, вычислимых за экспоненциальное время
обозначает (не рассматривавшийся нами) класс языков, вычислимых за экспоненциальное время 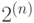 . Впрочем, наиболее популярна гипотеза о том, что все включения, изображенные на диаграмме — строгие.
. Впрочем, наиболее популярна гипотеза о том, что все включения, изображенные на диаграмме — строгие.
Задача 4.2. Машина Тьюринга с оракулом  — это МТ с дополнительной оракульной лентой, куда она (машина) может записывать слова, а затем за один такт работы проверять, принадлежит ли записанное на оракульной ленте слово языку
— это МТ с дополнительной оракульной лентой, куда она (машина) может записывать слова, а затем за один такт работы проверять, принадлежит ли записанное на оракульной ленте слово языку  . По двум сложностным классам
. По двум сложностным классам  и
и  можно определить класс
можно определить класс  таких языков, которые распознаются машинами из класса
таких языков, которые распознаются машинами из класса  с оракулами из
с оракулами из  .
.
Докажите, что 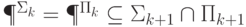 .
.
В классе 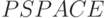 существуют полные задачи (относительно полиномиальной сводимости). Простейший вариант получается применением предыдущей теоремы.
существуют полные задачи (относительно полиномиальной сводимости). Простейший вариант получается применением предыдущей теоремы.
Задача 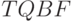 . Задается предикатом
. Задается предикатом


 есть истинная булева формула с кванторами (True Quantified Boolean Formula), т.е. формула вида
есть истинная булева формула с кванторами (True Quantified Boolean Formula), т.е. формула вида
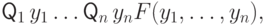
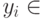 ,
,  — некоторая логическая формула, а
— некоторая логическая формула, а 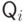 — либо
— либо 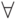 , либо
, либо  . По определению,
. По определению, 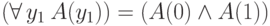 , а
, а 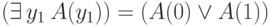 .
.Теорема 4.3. 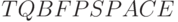 -полна.
-полна.
Доказательство. Построим сведение любого языка 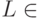 к задаче c TQBF. Для этого превратим МТ, вычисляющую результат игры (предикат
к задаче c TQBF. Для этого превратим МТ, вычисляющую результат игры (предикат 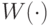 ), в схему, а ходы игроков закодируем булевыми переменными. Тогда наличие выигрышной стратегии у белых задается условием
), в схему, а ходы игроков закодируем булевыми переменными. Тогда наличие выигрышной стратегии у белых задается условием

 обозначает результат вычисления по схеме.
обозначает результат вычисления по схеме.Чтобы превратить  в булеву формулу, добавим новые переменные
в булеву формулу, добавим новые переменные  (значение, вычисленное при
(значение, вычисленное при  -м присваивании в схеме) и заменим
-м присваивании в схеме) и заменим  на формулу вида
на формулу вида

 — размер схемы,
— размер схемы, 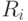 — правая часть
— правая часть  -го присваивания.
-го присваивания.После этой подстановки получим квантифицированную булеву формулу, которая истинна в точности для 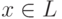 .
.

