Интерфейс и многопоточность

Итоги

Подведем некоторые итоги. Все задачи, для решения которых мы пишем программы, можно условно разделить на пять классов:

1. Задачи, не подлежащие распараллеливанию. К таким задачам относятся задачи, носящие принципиально последовательный характер. Примером является сложная в вычислительном отношении задача о "Ханойской башне", по правилам которой перенос колец может осуществляться только последовательно.
2. Потенциально распараллеливаемые задачи, для которых распараллеливание неэффективно. Для этого класса задач последовательные алгоритмы работают быстрее, чем параллельные. Связано это с тем, что организация параллельных вычислений требует накладных расходов. Эти расходы могут съедать весь выигрыш, полученный за счет параллелизма в вычислениях. Заметьте, отнесение задачи к этому классу зависит не только от задачи, но и от того, как вычислительный комплекс, на котором решается задача, реализует параллелизм.
3. Потенциально распараллеливаемые задачи, для которых известны эффективно работающие параллельные алгоритмы.
4. Потенциально распараллеливаемые задачи, для которых разработка эффективно работающих параллельных алгоритмов является проблемой, требующей творческого подхода.
5. Частично распараллеливаемые задачи, в которых можно выделить не подлежащую распараллеливания часть задачи и часть, потенциально распараллеливаемую.

Одной из целей учебного курса являлось рассмотрение широкого круга задач, позволяющее отнести задачу к тому или иному классу. При обосновании классификации можно использовать результаты анализа численных экспериментов, полученные при запуске программных проектов, создаваемых автором в ходе написания курса.

Программные проекты фактически являются частью курса, его дополнением, его поддержкой. Фрагменты проектов широко использовались в тексте курса. Тем не менее для программистов программный код не менее интересен, чем словесное описание. Исполняемому коду можно верить больше, чем словам. Поэтому все проекты, созданные автором для поддержки этого курса, с их кратким описанием будут доступны в интернете прежде всего на сайте открытого Интернет Университета ИТ – intuit.ru и на сайте НПО "Центрпрограммсистем" - cps.tver.ru

В качестве примера классификации рассмотрим задачу суммирования, широко обсуждаемую в учебном курсе. К какому из классов ее следует отнести? Для обоснования выводов был создан программный проект, а точнее, Решение (Solution) Sum, содержащее 5 проектов – DLL и 4 интерфейсных проекта.

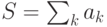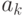В проектах рассматриваются три варианта вычисления суммы , где это :

• элементы массива;
• элементы бесконечного сходящегося ряда;
• элементы конечного ряда, представляющие значение некоторой функции .

Начнем с задачи суммирования элементов массива. Вот результаты, полученные на моем компьютере (64-х битный компьютер с 6 Гб оперативной памяти и 4-мя физическими ядрами) при запуске Windows проекта из Решения Sum:

Суммирование элементов массивов разного размера

Как можно видеть, все алгоритмы – последовательный и параллельные - прекрасно справляются с задачей. Время суммирования вплоть до массива, содержащего десять миллионов элементов, составляет менее 0,1 секунды. В такой ситуации параллельные алгоритмы не имеют никакого преимущества перед последовательным алгоритмом. Так что задачу нахождения суммы элементов массива, также как нахождение максимального элемента и другие подобные ей задачи, следует отнести ко второму классу, где применение параллельных алгоритмов хотя и возможно, но нецелесообразно на компьютерах подобного класса.

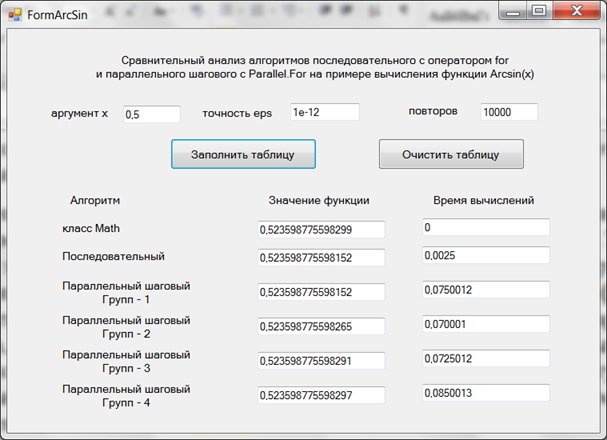
Приведу теперь результаты экспериментов для задачи суммирования бесконечного сходящегося ряда на примере вычисления значений функции Arcsin(x). Эта задача интересна еще и тем, что эффективный последовательный алгоритм использует рекуррентное соотношение для вычисления очередного члена суммы. При распараллеливании такого эффективного приема не существует. Рекуррентное соотношение хотя и можно построить для параллельного шагового алгоритма, но оно значительно сложнее в сравнении с последовательным вариантом. Учитывая еще, что последовательный алгоритм практически мгновенно решает эту задачу, то у параллельного алгоритма нет шансов выиграть, что и подтверждается результатами экспериментов:

Суммирование сходящегося ряда

Можно видеть, что как последовательный, так и параллельный алгоритм прекрасно справляются с задачей. Время многократного (10000 повторов) вычисления значения функции составляет менее 0,1 секунды. Но опять-таки параллельный алгоритм не имеет никакого преимущества перед последовательным алгоритмом. Так что и эту задачу следует отнести ко второму классу, где применение параллельных алгоритмов хотя и возможно, но нецелесообразно на компьютерах подобного класса.

Полагаю, что справедлива следующая гипотеза:

Задачи с линейной временной сложностью относятся ко второму классу.

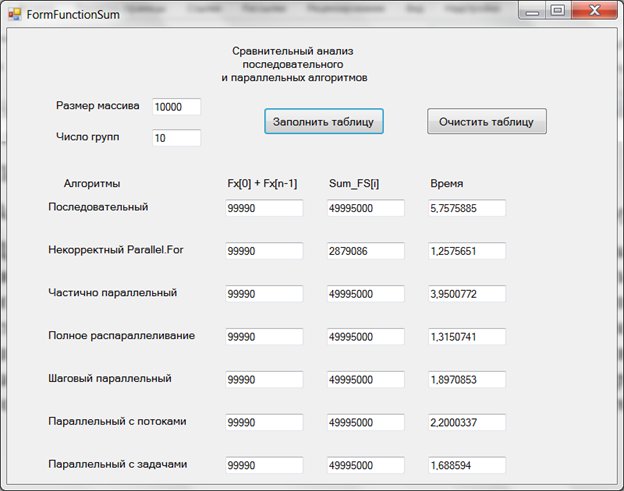
Для того чтобы параллельные алгоритмы выигрывали у последовательных алгоритмов исходная задача должно иметь по крайней мере квадратичную сложность. Суммирование конечного ряда, где каждый член ряда требует вычисления значения функции с линейной сложностью O(n), относится к подобным задачам. Вот как выглядят результаты эксперимента:

Суммирование конечного ряда

Рассматриваемую нами задачу, имеющую квадратичную временную сложность O(n2) следует отнести к третьему классу задач, допускающих эффективное распараллеливание.

Можно сделать и более общий вывод. Для потенциально распараллеливаемых задач со сложностью O(n2) и выше следует искать эффективные параллельные алгоритмы, позволяющие ощутимо сократить время решения задачи. Поиск таких алгоритмов не простая задача.