Проект "Компилятор формул"
В данном параграфе изучаются простейшие вопросы теории компиляции, рассматриваются языки простейших арифметических формул и стекового калькулятора, а также задача автоматического перевода с первого на второй.
Первым вариантом компилятора — средства для автоматического перевода программ, является рекурсивный компилятор формул — достаточно простой, но обладающий рядом недостатков.
Другой, значительно более общий подход к решению этой задачи, осуществляется во втором программном проекте — стековом компиляторе формул. Этот проект, кроме реализации компилятора, предусматривает также и реализацию интерпретатора арифметических формул. Исходные тексты упомянутых программ в значительной мере оптимизированы, а для облегчения работы над проектами используется утилита make.
Дополнительная информация о различных подходах к реализации компиляторов может быть найдена в книге [9].
Стековый калькулятор
Стековый калькулятор, как это следует из его названия, представляет из себя некоторый объект, использующий хорошо известный нам контейнер — стек. С формальной точки зрения стековый калькулятор — это класс, реализующий следующий интерфейс.
Интерфейс стекового калькулятора
interface StackCalc {
// Добавить число в стек.
void push(int val);
// Сложить.
int add() throws Exception;
// Вычесть.
int sub() throws Exception;
// Умножить.
int mul() throws Exception;
// Разделить.
int div() throws Exception;
// Показать вершину стека.
int top() throws Exception;
}Методы push и top хорошо известны и комментариев не требуют, а семантика остальных четырех такова: из стека извлекаются (с помощью метода pop ) два верхних числа, над ними выполняется указанная в названии метода арифметическая операция, а результат кладется обратно в стек (с помощью метода push ). При этом в качестве первого аргумента арифметической операции берется тот из двух извлеченных элементов, который был положен в стек раньше другого. Если в момент вызова одного из этих четырех методов глубина стека меньше двух, возникает исключительная ситуация. При реализации данного интерфейса на базе ограниченного вектора выполнение метода push также может привести к исключительной ситуации, связанной с переполнением стека.
Стековый калькулятор можно использовать для вычисления значений различных
арифметических выражений типа  . Нужно только написать
предварительно программу для вычисления значения.
. Нужно только написать
предварительно программу для вычисления значения.
С целью сокращения длины подобной программы будем записывать последовательность вызываемых методов в строку, разделяя их просто пробелом. Названия методов арифметических операций заменим на соответствующие им знаки действий ( +, -, * и / ), вместо вызова метода push с аргументом val будем записывать только его аргумент, а завершающий любую программу вызов метода top вообще включать в такую сокращенную запись программы не будем.
С использованием этих сокращений программа для вычисления выражения  примет вид 5 7 8 + * 25 +. Рисунок 12.1
показывает последовательность состояний стека стекового калькулятора при
выполнении этой программы.
примет вид 5 7 8 + * 25 +. Рисунок 12.1
показывает последовательность состояний стека стекового калькулятора при
выполнении этой программы.
В рассмотренном примере программа для стекового калькулятора была написана
по исходной формуле  нами. Основной задачей этого
параграфа
является реализация компилятора — программы, которая сможет
осуществлять преобразование формулы в программу для калькулятора автоматически.
нами. Основной задачей этого
параграфа
является реализация компилятора — программы, которая сможет
осуществлять преобразование формулы в программу для калькулятора автоматически.
С формальной точки зрения компилятор представляет собой программную
реализацию
некоторой функции  , действующей из множества цепочек одного
языка
, действующей из множества цепочек одного
языка 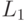 (в рассматриваемом случае это язык арифметических формул) в множество
цепочек другого
(в рассматриваемом случае это язык арифметических формул) в множество
цепочек другого 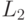 (язык программ стекового калькулятора)
таким образом, что
(язык программ стекового калькулятора)
таким образом, что  семантика цепочек
семантика цепочек  и
и 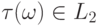 совпадает. Говоря другими словами,
компилятор
(часто называемый также транслятором ) реализует перевод с одного языка
на другой с сохранением смысла.
совпадает. Говоря другими словами,
компилятор
(часто называемый также транслятором ) реализует перевод с одного языка
на другой с сохранением смысла.
Напомним некоторые важнейшие определения, связанные с языками и грамматиками, которые были рассмотрены в "Высказывания и предикаты" .
Пусть  — некоторый алфавит,
— некоторый алфавит,  —
метаалфавит, т.е. какой-то
другой алфавит, не пересекающийся с
—
метаалфавит, т.е. какой-то
другой алфавит, не пересекающийся с  (
( 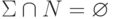 ).
Элементы метаалфавита
).
Элементы метаалфавита  называются метасимволами. Грамматикой
называются метасимволами. Грамматикой  называется набор (
называется набор (  ), где
), где  — множество символов,
— множество символов,  — множество метасимволов,
— множество метасимволов,  — множество правил
вывода вида:
— множество правил
вывода вида:  , где
, где  — какой-то
метасимвол,
— какой-то
метасимвол, 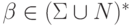 — произвольная цепочка над
объединением двух
алфавитов, и для каждого
— произвольная цепочка над
объединением двух
алфавитов, и для каждого  встречается хотя бы одно
правило с
встречается хотя бы одно
правило с  в левой части (до стрелочки), а
в левой части (до стрелочки), а 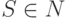 —
так называемый стартовый метасимвол.
—
так называемый стартовый метасимвол.
Содержательно каждое правило грамматики имеет смысл подстановки. Например,
строка 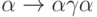 означает возможность
замены
метасимвола
означает возможность
замены
метасимвола  на цепочку
на цепочку  .
Начав со стартового
символа и пользуясь различными правилами грамматики, мы можем получать
различные цепочки из символов, которые называются выводимыми
цепочками.
.
Начав со стартового
символа и пользуясь различными правилами грамматики, мы можем получать
различные цепочки из символов, которые называются выводимыми
цепочками.
Заметим, что если в цепочке встречается метасимвол, то ее можно
преобразовать
дальше, применив одно из правил грамматики с этим метасимволом в левой части.
Если же метасимволов в цепочке не осталось, то процесс ее преобразования
закончен и больше с цепочкой ничего сделать нельзя. По этой причине обычные
символы (из алфавита  ) часто называют терминалами,
а метасимволы (из
) часто называют терминалами,
а метасимволы (из  ) — нетерминалами.
) — нетерминалами.
Языком 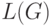 , порожденным грамматикой
, порожденным грамматикой  ,
называется множество всех
терминальных выводимых цепочек.
,
называется множество всех
терминальных выводимых цепочек.
Для задания грамматики часто используют очень наглядную форму представления,
называемую нормальной формой Бэкуса-Наура (НФБН).
Набор правил  задают при этом в виде совокупности правил со
стрелочками,
перечисляющими все возможные цепочки, на которые может быть заменен
каждый из метасимволов грамматики в процессе вывода, а стартовым метасимволом
считается тот, который присутствует в левой части самого первого правила.
задают при этом в виде совокупности правил со
стрелочками,
перечисляющими все возможные цепочки, на которые может быть заменен
каждый из метасимволов грамматики в процессе вывода, а стартовым метасимволом
считается тот, который присутствует в левой части самого первого правила.
Возьмем в качестве алфавита  множество, состоящее
из четырех знаков
арифметических операций (
множество, состоящее
из четырех знаков
арифметических операций ( 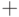 ,
, 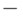 ,
,  и
и 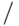 ) и 26-и
идентификаторов от
) и 26-и
идентификаторов от  до
до  , которыми будут
обозначаться произвольные
целые числа:
, которыми будут
обозначаться произвольные
целые числа:  .
.
Тогда язык  будет представлять из себя все возможные
программы
для стекового калькулятора, включая и неправильные.
Например, пустая цепочка
будет представлять из себя все возможные
программы
для стекового калькулятора, включая и неправильные.
Например, пустая цепочка  означает
вызов единственного метода pop, что приведет к возникновению
исключительной ситуации. Принадлежащая этому языку цепочка 2 + также
соответствует некорректной программе, ибо в момент вызова метода add
в стеке будет содержаться только один элемент.
означает
вызов единственного метода pop, что приведет к возникновению
исключительной ситуации. Принадлежащая этому языку цепочка 2 + также
соответствует некорректной программе, ибо в момент вызова метода add
в стеке будет содержаться только один элемент.
Для описания языка правильных программ для стекового калькулятора можно
воспользоваться следующей грамматикой 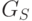 .
.

Именно язык  мы и будем рассматривать, как язык
правильных программ
для стекового калькулятора.
мы и будем рассматривать, как язык
правильных программ
для стекового калькулятора.

