НОУ ИНТУИТ | Основы информатики и программирования. Лекция 8: Проектирование цикла при помощи инварианта

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный индустриальный университет

Опубликован: 27.09.2006 | Доступ: свободный | Студентов: 3332 / 380 | Оценка: 4.17 / 3.79 | Длительность: 24:17:00

Темы: Программирование, Образование

Специальности: Программист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Условия правильности цикла. Теория воздушного шарика. Устранение конъюнктивного члена. Замена константы переменной. Расширение области значения переменной.

В предыдущем параграфе мы уже познакомились с техникой проектирования цикла при помощи инварианта, позволяющей значительно упростить написание программ. Вопросы нахождения инвариантов циклов и доказательства правильности получающихся программ — основная тематика данного параграфа.

Условия правильности цикла

Теоремой, на которой базируется схема проектирования цикла при помощи инварианта, является следующее утверждение, которое мы примем без доказательства. Его истинность может быть выведена из свойств преобразователя предикатов и определения оператора цикла 6.12.

Теорема 8.1. Если

$\{Q\}\ "S0;"\ \{I\}$ ,
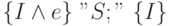$\{I \land e\}\ "S;"\ \{I\}$ ,
$(I \land !e) \Rightarrow R$ ,
$I \land e \Rightarrow h > 0$ и
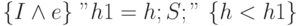$\{I \land e \}\ "h1=h; S;"\ \{h<h1\}$ ,

то спецификация программы $\{Q\}\ "S0;while(e)S;"\ \{R\}$ является тавтологией.

Докажем с помощью этой теоремы правильность некоторых программ, построенных в предыдущем параграфе.

Текст программы

public class MulI {
    public static void main(String[] args) throws Exception {    
        int a = Xterm.inputInt("a -> ");
        int b = Xterm.inputInt("b -> ");
        int x = a, y = b, z = 0;
        while (y > 0) { 
            if ((y&1) == 0) {
                y >>>= 1; x +=  x;
            } else {
                y  -=  1; z +=  x;
            }
        }
        Xterm.println("a * b = " + z);
    }
}

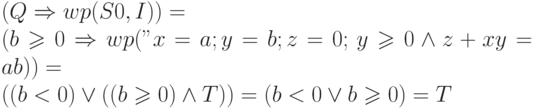
$(Q \Rightarrow wp(S0, I)) = \\ (b \geqslant 0 \Rightarrow wp("x=a;y=b;z=0;", y \geqslant 0 \land z + xy = ab)) = \\ ((b < 0) \lor ((b\geqslant 0)\land T)) = (b<0 \lor b\geqslant 0) = T$
Для того чтобы проверить, что предикат $I\land e \Rightarrow wp(S, I)$ является тавтологией, вычислим предварительно .
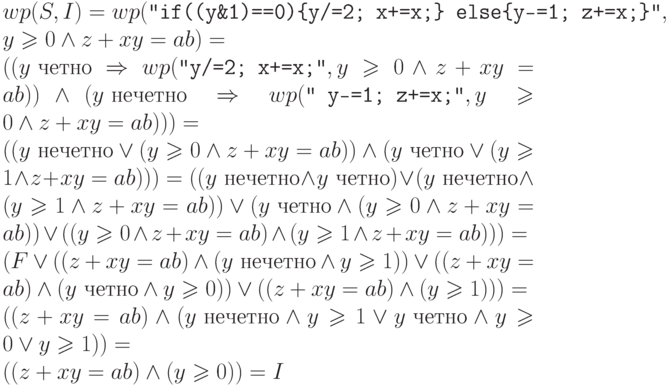
$wp(S, I) = wp(\Cmd{if((y\&1)==0)\{y/=2; x+=x;\} else\{y-=1; z+=x;\}},\\ y \geqslant 0 \land z + xy = ab) = \\ ((y \mbox{\ четно}\Rightarrow wp(\Cmd{y/=2; x+=x;}, y \geqslant 0 \land z + xy = ab)) \land (y \mbox{\ нечетно}\Rightarrow wp(\Cmd{ y-=1; z+=x;}, y \geqslant 0 \land z + xy = ab))) = \\ ((y \mbox{\ нечетно} \lor (y \geqslant 0 \land z + xy = ab)) \land (y \mbox{\ четно} \lor (y \geqslant 1 \land z + xy = ab))) = ( (y \mbox{\ нечетно}\land y \mbox{\ четно})\lor (y \mbox{\ нечетно}\land (y \geqslant 1 \land z + xy = ab))\lor (y \mbox{\ четно} \land (y \geqslant 0 \land z + xy = ab))\lor ((y \geqslant 0 \land z + xy = ab)\land (y \geqslant 1 \land z + xy = ab)) ) = \\ ( F\lor ((z + xy = ab)\land (y \mbox{\ нечетно}\land y \geqslant 1))\lor ((z + xy = ab)\land (y \mbox{\ четно}\land y \geqslant 0))\lor ((z + xy = ab)\land (y \geqslant 1)) ) = \\ ((z + xy = ab)\land( y \mbox{\ нечетно}\land y \geqslant 1\lor y \mbox{\ четно}\land y \geqslant 0 \lor y \geqslant 1)) = \\ ((z + xy = ab)\land(y\geqslant 0)) = I$

Далее имеем
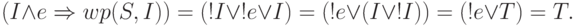
$(I\land e \Rightarrow wp(S, I)) = (!I\lor!e\lor I) = (!e \lor (I\lor!I)) = (!e \lor T) = T.$
$(I \land !e \Rightarrow R) = (!I \lor e \lor R) = \\ (y<0\lor z+xy\ne ab\lor y >0 \lor z=ab) = \\ (y<0 \lor y>0 \lor z=ab \lor z+xy\ne ab).$

Получившийся предикат представляет собой дизъюнкцию четырех членов и, очевидно, истинен, если истинны первый или второй из этих членов. В противном случае , и предикат принимает вид $(z=ab \lor z\ne ab) = T$ . Таким образом, $(I \land !e \Rightarrow R)$ — тавтология.
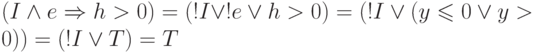$(I \land e \Rightarrow h > 0) = (!I \lor !e \lor h >0) = (!I\lor (y \leqslant 0 \lor y>0)) = (!I \lor T) = T$ .
Для проверки последнего условия найдем

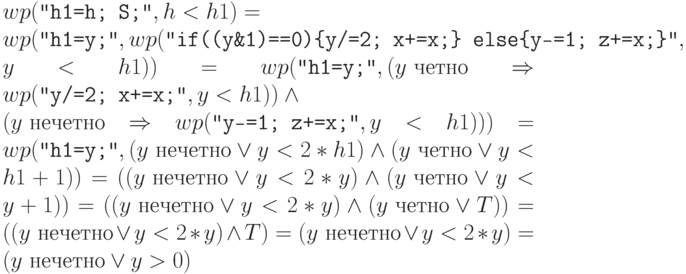
$wp(\Cmd{h1=h; S;}, h<h1) = \\ wp(\Cmd{h1=y;}, wp(\Cmd{if((y\&1)==0)\{y/=2; x+=x;\} else\{y-=1; z+=x;\}},\\ y<h1)) = wp(\Cmd{h1=y;},(y \mbox{\ четно}\Rightarrow wp(\Cmd{y/=2; x+=x;},y<h1))\land\\ (y \mbox{\ нечетно}\Rightarrow wp(\Cmd{y-=1; z+=x;},y<h1))) = wp(\Cmd{h1=y;},(y \mbox{\ нечетно}\lor y<2*h1)\land (y \mbox{\ четно}\lor y<h1+1)) = ((y \mbox{\ нечетно}\lor y<2*y)\land (y \mbox{\ четно}\lor y<y+1)) = ((y \mbox{\ нечетно}\lor y<2*y)\land (y \mbox{\ четно}\lor T)) = ((y \mbox{\ нечетно}\lor y<2*y)\land T) = (y \mbox{\ нечетно}\lor y<2*y) = (y \mbox{\ нечетно}\lor y>0)$

Тогда имеем

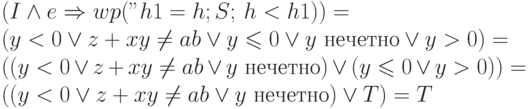
$(I\land e \Rightarrow wp("h1=h; S;", h<h1))= \\ (y<0 \lor z + xy \ne ab\lor y \leqslant 0 \lor y \mbox{\ нечетно}\lor y>0)= \\ ((y<0 \lor z + xy \ne ab\lor y \mbox{\ нечетно})\lor (y \leqslant 0 \lor y>0))= \\ ((y<0 \lor z + xy \ne ab\lor y \mbox{\ нечетно})\lor T) = T$

что завершает доказательство правильности написанной программы.

Докажем частично правильность еще одной построенной в предыдущем параграфе программы.

Текст программы

public class Gcd {
    public static void main(String[] args) throws Exception {
        int x = Xterm.inputInt("x -> ");
        int y = Xterm.inputInt("y -> ");
        Xterm.print("gcd(" + x + "," + y + ") =");
        while ( (x != 0) && (y != 0) ) {
            if (x >= y) x -= y;
            else        y -= x;
        } 
        Xterm.println(" " + (x+y));
    }
}

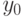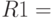Если в качестве ограничивающей функции взять $h=x\cdot y$ , то правильность полученной программы легко может быть доказана. Обозначим через x_0 и y_0 начальные значения переменных и , удовлетворяющих предусловию $Q=(x \in \mathbb{Z}_M^+\land y \in \mathbb{Z}_M^+\land (x,y) \ne (0,0))$ . 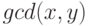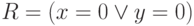Заметим также, что постусловие программы в целом может быть записано в виде предиката R1 = ( напечатан gcd(x,y) ), а постусловием цикла является предикат $R=(x=0\lor y=0)$ .

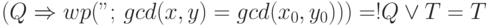$(Q \Rightarrow wp(";", gcd(x,y)=gcd(x_0,y_0))) = !Q \lor T = T$ .
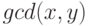Сохранение инварианта после выполнения тела цикла следует из -инвариантности . Формальную проверку проведите самостоятельно.
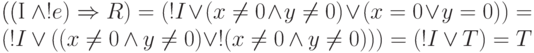
$((I \land !e) \Rightarrow R) = (!I\lor (x\ne 0\land y\ne 0) \lor (x=0 \lor y=0)) = (!I \lor ((x\ne 0\land y\ne 0) \lor !(x\ne 0\land y\ne 0))) = (!I \lor T) = T$
Формальное доказательство проведите самостоятельно.
Формальное доказательство проведите самостоятельно.
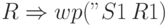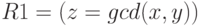Для завершения доказательства правильности программы необходимо еще показать, что является тавтологией $R \Rightarrow wp("S1", R1)$ . Так как формального определения операторов печати мы не рассматривали, будем считать, что предикат , а 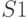имеет вид .
$(R \Rightarrow wp("S1", R1)) = ((x=0\lor y=0)\Rightarrow(x+y = gcd(x,y)))= (!(x=0\lor y=0) \lor (gcd(x,y) = x+y))$

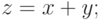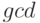Полученная дизъюнкция истинна, если ложно условие $(x=0\lor y=0)$ . В противном случае один из аргументов функции gcd равен нулю и по соответствующему свойству наименьшего общего делителя истинным является второй дизъюнктивный член, что завершает доказательство правильности программы.

Дальше >>

Авторизоваться

Основы информатики и программирования

Проектирование цикла при помощи инварианта

Условия правильности цикла

Вопросы и ответы