Свойства замкнутости класса автоматных языков. Неавтоматные языки
Теорема о разрастании для автоматных языков
До сих пор мы встречались лишь с автоматными языками и накопили достаточно много средств для доказательства того, что некоторый язык является автоматным. Для этого, например, достаточно построить для него регулярное выражение или получить его с помощью различных рассмотренных выше операций из заведомо автоматных языков. В этом разделе мы установим некоторое необходимое условие, которому удовлетворяют все автоматные языки. После этого, проверив, что некоторый язык этому условию не удовлетворяет, можно заключить, что он не является автоматным.
Теорема 6.3. (о разрастании для автоматных языков)
Пусть L - бесконечный автоматный язык. Тогда существует такая константа n, что любое слово 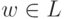 длины |w| > n можно разбить на три части x, y и z так, что w = xyz и
длины |w| > n можно разбить на три части x, y и z так, что w = xyz и
- |xy| <= n ;
- |y| > 0 ;
- для любого m >= 0 слово wm = x ym z принадлежит языку L.
(Здесь 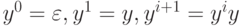 ).
).
Доказательство Так как язык L автоматный, то существует ДКА  , распознающий L.
Пусть |Q|= n и слово
, распознающий L.
Пусть |Q|= n и слово 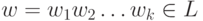 имеет длину k > n. Рассмотрим путь
имеет длину k > n. Рассмотрим путь  в диаграмме A, который несет слово w. Очевидно, что среди первых (n+1) состояний этого
пути хотя бы одно встречается дважды. Выберем первое из таких состояний
в диаграмме A, который несет слово w. Очевидно, что среди первых (n+1) состояний этого
пути хотя бы одно встречается дважды. Выберем первое из таких состояний 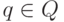 . Тогда для
некоторой пары чисел l < j <= n имеем
. Тогда для
некоторой пары чисел l < j <= n имеем 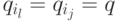 . Пусть x=w1w2 ... wl - это префикс w, который переводит q0 в
. Пусть x=w1w2 ... wl - это префикс w, который переводит q0 в 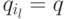 ,
, 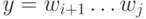 - это подслово w, которое переводит
- это подслово w, которое переводит 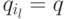 в
в 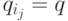 , и
, и 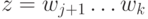 - это суффикс w, который переводит
- это суффикс w, который переводит 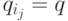 в
в 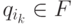 . x и z могут быть пусты, но |y| = j-l >= 1.
Длина |xy| = j <= n. Таким образом, условия (1) и (2) теоремы выполнены.
Нетрудно убедиться и в выполнении условия (3). Действительно, выбросив из пути p
цикл
. x и z могут быть пусты, но |y| = j-l >= 1.
Длина |xy| = j <= n. Таким образом, условия (1) и (2) теоремы выполнены.
Нетрудно убедиться и в выполнении условия (3). Действительно, выбросив из пути p
цикл 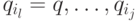 , получим путь p0 из q0 в
, получим путь p0 из q0 в  , который несет
слово xz, а повторив этот цикл m раз, получим путь p0 из q0 в
, который несет
слово xz, а повторив этот цикл m раз, получим путь p0 из q0 в 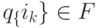 , который несет
слово xym z. Следовательно, для любого m >= 0
, который несет
слово xym z. Следовательно, для любого m >= 0  .
.
Содержательно, эта теорема утверждает, что у всякого достаточно длинного слова из автоматного языка имеется непустое подслово, которое можно вырезать или повторить сколько угодно раз, оставаясь внутри языка. Как, используя теорему ref{th-razr}, доказать, что некоторый язык L не является автоматным? Это можно сделать, используя схему доказательства "от противного":
- Предположим, что L автоматный язык. Тогда для него имеется константа n из утверждения теоремы ref{th-razr}.
- Определим по n некотрое "специальное" слово w из L длины > n и докажем, что для любого разбиения w = xyz, удовлетворяющего условиям (1) и (2) теоремы, найдется такое k >= 0, что слово wk=xyk z не принадлежит L.
- На основании полученного противоречия делаем вывод, что L - не автоматный язык.
Разумеется, в этой схеме самым сложным является выбор "специального" слова w в пункте
(2). Что касается, подбора такого k >= 0, для которого  , то, как правило,
достаточно рассмотреть k = 0 или k = 2.
, то, как правило,
достаточно рассмотреть k = 0 или k = 2.
Примеры неавтоматных языков
Рассмотрим несколько примеров применения теоремы о разрастании.
Пример 6.4. Покажем, что язык L1 ={ w =0i 1i | i >= 1 } не является автоматным.
Предположим, что он автоматный. Тогда для него имеется n из утверждения теоремы 6.3.
Рассмотрим следующее ("специальное" !) слово w = 0n 1n. Очевидно, что  .
Предположим, что существует разбиение w = xyz, удовлетворяющего условиям
(1) и (2) теоремы. Так как по условию (2) |xy| <= n, то y = 0i для некоторого i>0.
Но тогда слово
.
Предположим, что существует разбиение w = xyz, удовлетворяющего условиям
(1) и (2) теоремы. Так как по условию (2) |xy| <= n, то y = 0i для некоторого i>0.
Но тогда слово  , что противоречит условию (3) теоремы.
Следовательно язык L1 не автоматный.
, что противоречит условию (3) теоремы.
Следовательно язык L1 не автоматный.
Пример 6.5. Покажем, что язык СКОБ правильных скобочных последовательностей в алфавите { (, ) } не является автоматным.
Схема доказательства та же. В качестве специального слова выберем слово w = (n )n, оно, очевидно, принадлежит СКОБ. Тогда для всякого разбиения w = xyz такого, что |xy| <= n слово y = (i для некоторого i>0. И, как и в предыдущем
примере, слово 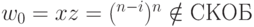 , что противоречит условию (3) теоремы. Следовательно, язык СКОБ не автоматный.
, что противоречит условию (3) теоремы. Следовательно, язык СКОБ не автоматный.
Пример 6.6. Покажем, что язык L2 ={ w =0i 1j | i <= 2j+1 } не является автоматным.
Здесь, предположив, что L2 автоматный язык и зафиксировав константу n из теоремы 6.3, рассмотрим слово 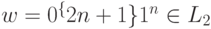 . Для всякого разбиения w = xyz такого, что |xy| <= n слово y = 0i для некоторого i>0.
Рассмотрим слово w2 = x y2 z = 0{2n+1+i}1n. Но
. Для всякого разбиения w = xyz такого, что |xy| <= n слово y = 0i для некоторого i>0.
Рассмотрим слово w2 = x y2 z = 0{2n+1+i}1n. Но 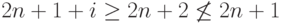 .
Следовательно,
.
Следовательно, 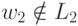 и язык L2 не является автоматным.
и язык L2 не является автоматным.
Пример 6.7. Рассмотрим язык "квадратов" в унарном алфавите { | }:
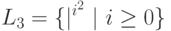
Здесь, предположив, что L3 автоматный язык и зафиксировав константу n из
теоремы 6.3, рассмотрим слово w = |{n2}.
Для всякого разбиения w = xyz такого, что |xy| <= n слово y = |i для некоторого 0 < i <= n.
Тогда  . Но n2 - i >= n2 -n > n2 -2n +1 =(n-1)2.
Следовательно, n2 - i не является полным квадратом и
. Но n2 - i >= n2 -n > n2 -2n +1 =(n-1)2.
Следовательно, n2 - i не является полным квадратом и 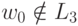 ,
т.е. язык "квадратов" L3 не является автоматным.
,
т.е. язык "квадратов" L3 не является автоматным.
Пример 6.8. Рассмотрим язык "простых чисел" в унарном алфавите { | }:
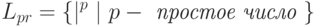
Предположим, что Lpr - автоматный язык и зафиксируем для него константу n из
теоремы 6.3. Выберем простое число p > n и рассмотрим слово w = |p.
Пусть w = xyz - произвольное разбиение w такое, что |xy| <= n. Тогда для некоторого 0 < i <= n
слово y = |i и xz = |p -i. Положим k = p - i и рассмотрим слово wk = x yk z. Его длина p' равна |x| +k|y| + |z|= (p-i)(i+1). Так как 1 <= i < n+1 <= p,
то p' - составное число и 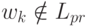 . Следовательно, Lpr - не автоматный язык. Заметим, что в этом примере k выбирается для каждого n
по-своему.
. Следовательно, Lpr - не автоматный язык. Заметим, что в этом примере k выбирается для каждого n
по-своему.
Еще один прием доказательства неавтоматности языка L состоит в том, чтобы вместо L рассмотреть некоторый язык L' = op(L,L1,... , Lk), полученный из L и автоматных языков L1,... , Lk с помощью операций op, сохраняющих автоматность. Если доказать, что L' не является автоматным, то и исходный язык L не автоматен.
Пример 6.9. Рассмотрим язык 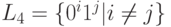 .
.
Пусть L5= {0i1j | i >= 1, j >= 1}.
Очевидно, что язык L5 автоматный.
Нетрудно заметить, что его пересечение с дополнением L4 совпадает с языком L1
из примера 6.4, т.е. 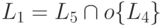 .
Так как мы установили, что L1 не автоматный, то и L4 не является автоматным.
.
Так как мы установили, что L1 не автоматный, то и L4 не является автоматным.
Являются ли условия теоремы 6.3 достаточными для того, чтобы язык оказался автоматным? Следующий пример показывает, что ответ на этот вопрос отрицателен.
Пример 6.10.Пусть L6 ={cr ai bi | r >= 1 , i>= 0 }, L7= { aibj | i >= 0, j >= 0}.
Рассмотрим язык 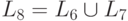 .
.
Для этого языка можно в качестве n выбрать 1. Каждое слово w из L8 принадлежит L6 или L7. Если слово 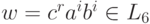 , то оно
представимо в виде xyz, где
, то оно
представимо в виде xyz, где  .
Тогда w0 = z= cr-1 ai bi ( r >= 1, i >= 1 ) и при r=1 слово
.
Тогда w0 = z= cr-1 ai bi ( r >= 1, i >= 1 ) и при r=1 слово 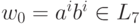 ,
а при r > 1, очевидно,
,
а при r > 1, очевидно, 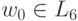 . При k >= 1 имеем
. При k >= 1 имеем 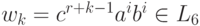 .
Если слово
.
Если слово 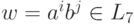 и i >= 1, то его можно представить как
в виде xyz, где
и i >= 1, то его можно представить как
в виде xyz, где 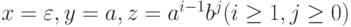 и для каждого k>= 0
и для каждого k>= 0 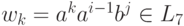 . Если же i =0, то w= bj ( j >= 1 ) и его можно разбить
на части
. Если же i =0, то w= bj ( j >= 1 ) и его можно разбить
на части  . И в этом случае
для каждого k >= 0
. И в этом случае
для каждого k >= 0  . Во всех случаях
. Во всех случаях 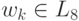 и, следовательно
язык L8 удовлетворяет условиям теоремы 6.3. Но этот язык не автоматный.
Действительно, пусть
и, следовательно
язык L8 удовлетворяет условиям теоремы 6.3. Но этот язык не автоматный.
Действительно, пусть 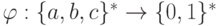 - это гомоморфизм,
заданный как
- это гомоморфизм,
заданный как  .
Тогда
.
Тогда 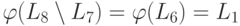 из примера 6.4. Так как язык L7 является автоматным, а L1 - нет, то и язык L8 не является автоматным.
из примера 6.4. Так как язык L7 является автоматным, а L1 - нет, то и язык L8 не является автоматным.
