|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Жадные алгоритмы и матроиды
Теорема 2. Если 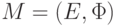 - матроид, то для
любой весовой функции
- матроид, то для
любой весовой функции 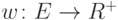 множество
множество  , найденное
алгоритмом СПО, будет множеством наибольшего веса из
, найденное
алгоритмом СПО, будет множеством наибольшего веса из  .
Если же
.
Если же  не является матроидом, то найдется такая
функция
не является матроидом, то найдется такая
функция 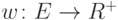 , что
, что  не будет множеством
наибольшего веса из
не будет множеством
наибольшего веса из  .
.
Доказательство. Предположим, что 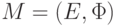 является матроидом
и
является матроидом
и  - множество, построенное
алгоритмом СПО, причем
- множество, построенное
алгоритмом СПО, причем 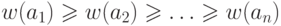 .
Очевидно,
.
Очевидно,  является базой матроида.
Пусть
является базой матроида.
Пусть 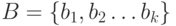 - любое другое независимое множество
и
- любое другое независимое множество
и  .
Так как
.
Так как  - база, то
- база, то  .
Покажем, что
.
Покажем, что 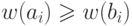 для каждого
для каждого 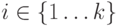 .
Действительно, положим
.
Действительно, положим  ,
, 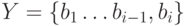 для некоторого
для некоторого  .
Согласно условию (2) определения матроида, в множестве
.
Согласно условию (2) определения матроида, в множестве  имеется такой элемент
имеется такой элемент 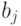 , что
, что  и
множество
и
множество  - независимое. В соответствии с алгоритмом,
элементом наибольшего веса, который может быть добавлен к
- независимое. В соответствии с алгоритмом,
элементом наибольшего веса, который может быть добавлен к  так,
чтобы получилось независимое множество, является
так,
чтобы получилось независимое множество, является 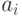 .
Следовательно,
.
Следовательно,  .
.
Теперь предположим, что 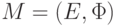 не является матроидом.
Допустим
сначала, что нарушается условие (1), т.е. существуют такие подмножества
не является матроидом.
Допустим
сначала, что нарушается условие (1), т.е. существуют такие подмножества  и
и  множества
множества  , что
, что 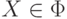 ,
, 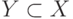 и
и 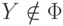 . Определим
функцию
. Определим
функцию  следующим образом:
следующим образом:

Алгоритм СПО сначала будет рассматривать все элементы
множества  .
Так как
.
Так как 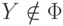 , то не все они войдут в построенное
алгоритмом
множество
, то не все они войдут в построенное
алгоритмом
множество  . Следовательно, w(A) < |Y|. В то же
время имеется
множество
. Следовательно, w(A) < |Y|. В то же
время имеется
множество 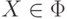 , такое, что
, такое, что 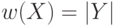 . Таким
образом,
в этом случае алгоритм СПО строит не оптимальное множество. Если же
условие (1) выполнено, а не выполняется условие (2), то существуют такие
подмножества
. Таким
образом,
в этом случае алгоритм СПО строит не оптимальное множество. Если же
условие (1) выполнено, а не выполняется условие (2), то существуют такие
подмножества  и
и  множества
множества  ,
что
,
что 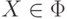 ,
, 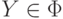 , |X| < |Y|
и
, |X| < |Y|
и 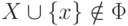 для каждого
для каждого  . Выберем такое
. Выберем такое  ,
что
,
что 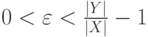 , и определим
функцию
, и определим
функцию  следующим образом:
следующим образом:
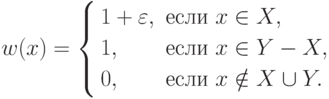
Алгоритм СПО сначала выберет все элементы множества  , а затем
отвергнет все элементы из
, а затем
отвергнет все элементы из  . В результате будет построено
множество
. В результате будет построено
множество  с весом
с весом 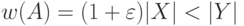 ,
которое не
является оптимальным, так как
,
которое не
является оптимальным, так как 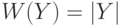 .
.
Максимизирующий алгоритм Крускала - это алгоритм СПО, применяемый к семейству ациклических множеств ребер графа. Из теорем 1 и 2 следует, что он действительно решает задачу об оптимальном каркасе. В то же время существует много жадных алгоритмов, не являющихся алгоритмами типа СПО. Примером может служить алгоритм Прима. Эти алгоритмы не попадают под действие теоремы Радо-Эдмондса, для их обоснования нужна иная аргументация.
Если для некоторой конкретной задачи удалось установить применимость
к ней
алгоритма СПО, это не значит, что все проблемы позади. Этот алгоритм
внешне очень прост, но он включает операцию проверки принадлежности
множества семейству  , эффективное выполнение которой может
потребовать дополнительных усилий. В алгоритме Крускала, например, для
этого применяются специальные структуры данных. Ниже рассмотрим еще один
пример, когда для успешного решения задачи алгоритм СПО комбинируется
с методом увеличивающих путей для задачи о паросочетании, рассмотренным в
"лекции 12"
.
, эффективное выполнение которой может
потребовать дополнительных усилий. В алгоритме Крускала, например, для
этого применяются специальные структуры данных. Ниже рассмотрим еще один
пример, когда для успешного решения задачи алгоритм СПО комбинируется
с методом увеличивающих путей для задачи о паросочетании, рассмотренным в
"лекции 12"
.
