|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Пространство циклов графа
Квазициклы
В этом разделе слово "цикл" мы будем понимать несколько иначе, чем до сих пор. Именно, циклом будем называть граф, у которого одна компонента связности является простым циклом, а остальные - изолированными вершинами. На рис. 7.1 показано, что в результате сложения двух циклов иногда получается цикл. Это не всегда так (например, когда складываемые циклы не имеют общих ребер), но все-таки графы, которые можно получить, складывая циклы, обладают определенными особенностями. На этом основан алгебраический подход к изучению устройства множества циклов графа.
Рассмотрим некоторый граф 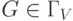 . Среди его
остовных
подграфов, возможно, имеется некоторое количество циклов. Обозначим
через
. Среди его
остовных
подграфов, возможно, имеется некоторое количество циклов. Обозначим
через ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) подпространство пространства подграфов, порождаемое
всеми этими
циклами.
подпространство пространства подграфов, порождаемое
всеми этими
циклами. ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) называется пространством циклов графа
называется пространством циклов графа  .
Оно содержит граф
.
Оно содержит граф  (если в
(если в  нет циклов,
то
нет циклов,
то  является единственным элементом пространства циклов), а все
остальные его элементы - это всевозможные линейные комбинации циклов
графа
является единственным элементом пространства циклов), а все
остальные его элементы - это всевозможные линейные комбинации циклов
графа  . Заметим, что коэффициентами в линейных комбинациях
являются
элементы множества
. Заметим, что коэффициентами в линейных комбинациях
являются
элементы множества  , поэтому речь идет на самом деле просто
о всевозможных суммах циклов.
, поэтому речь идет на самом деле просто
о всевозможных суммах циклов.
Остовный подграф, у которого степени всех вершин четны, называется квазициклом. Оказывается,
множество ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) состоит в точности из всех
квазициклов графа
состоит в точности из всех
квазициклов графа  . Прежде чем доказать это, покажем сначала, что
множество всех квазициклов замкнуто относительно сложения.
. Прежде чем доказать это, покажем сначала, что
множество всех квазициклов замкнуто относительно сложения.
Лемма 1. Сумма двух квазициклов есть квазицикл.
Доказательство. Пусть 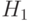 и
и 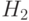 - квазициклы.
Рассмотрим произвольную вершину
- квазициклы.
Рассмотрим произвольную вершину  , и пусть ее степени
в
, и пусть ее степени
в 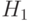 и
и 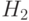 равны соответственно
равны соответственно 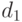 и
и 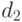 .
Тогда степень вершины
.
Тогда степень вершины  в графе
в графе  будет равна
будет равна 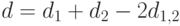 , где
, где 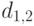 - число
вершин, с которыми
- число
вершин, с которыми  смежна в обоих графах
смежна в обоих графах 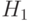 и
и 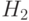 .
Отсюда видно, что число
.
Отсюда видно, что число  четно, если четны оба
числа
четно, если четны оба
числа 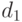 и
и 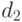 .
.
Следующая лемма объясняет строение квазициклов.
Лемма 2. Любой квазицикл с непустым множеством ребер является объединением простых циклов, не имеющих общих ребер.
Доказательство. В квазицикле  в любой компоненте
связности, состоящей не менее чем из двух вершин, степени всех вершин не
меньше 2, следовательно, в нем есть цикл, а, значит, и простой цикл. Взяв
какой-нибудь простой цикл в
в любой компоненте
связности, состоящей не менее чем из двух вершин, степени всех вершин не
меньше 2, следовательно, в нем есть цикл, а, значит, и простой цикл. Взяв
какой-нибудь простой цикл в  и удалив его ребра
из
и удалив его ребра
из  ,
снова получим квазицикл. Если в этом новом квазицикле есть хотя бы
одно ребро, то в нем также имеется простой цикл, и т.д. В конце концов,
когда останется пустой граф, будет построено семейство простых циклов, не
имеющих общих ребер и в совокупности содержащих все ребра графа
,
снова получим квазицикл. Если в этом новом квазицикле есть хотя бы
одно ребро, то в нем также имеется простой цикл, и т.д. В конце концов,
когда останется пустой граф, будет построено семейство простых циклов, не
имеющих общих ребер и в совокупности содержащих все ребра графа  .
.
Теорема 1. Граф принадлежит множеству ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) тогда и только тогда, когда он
является квазициклом графа
тогда и только тогда, когда он
является квазициклом графа  .
.
Доказательство. Всякий цикл является квазициклом. Так как элементы ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) - это суммы циклов, то, по лемме 1, все
они - квазициклы. Обратное
утверждение (каждый квазицикл принадлежит
- это суммы циклов, то, по лемме 1, все
они - квазициклы. Обратное
утверждение (каждый квазицикл принадлежит ![C[G]](/sites/default/files/tex_cache/40f7582c1aef765b7b3649cd37f50564.png) )
следует из леммы 2,
так как объединение циклов, не имеющих общих ребер, совпадает
с их суммой.
)
следует из леммы 2,
так как объединение циклов, не имеющих общих ребер, совпадает
с их суммой.
