|
Скажите, пожалуйста, можно ли еще получить документ о прохождении курса ("Графы и алгоритмы", декабрь 2020) после предоставления всех дополнительных необходимых документов? |
Поиск в глубину
Шарниры
В качестве примера задачи, для эффективного решения которой можно
использовать основное свойство DFS-дерева, выражаемое теоремой 1,
рассмотрим задачу выявления шарниров в графе. Напомним, что шарниром
называется вершина, при удалении которой увеличивается число компонент
связности. Отсутствие поперечных ребер относительно DFS-дерева позволяет
очень просто узнать, является ли стартовая вершина  (корень
этого дерева) шарниром.
(корень
этого дерева) шарниром.
Лемма 1. Стартовая вершина а является шарниром графа тогда и
только тогда, когда ее степень в DFS-дереве больше  .
.
Доказательство. Если вершину  удалить из дерева, то оно
распадется на поддеревья, называемые ветвями. Число ветвей равно степени
вершины
удалить из дерева, то оно
распадется на поддеревья, называемые ветвями. Число ветвей равно степени
вершины  в дереве. Так как поперечных ребер нет, то вершины из
разных ветвей не могут быть смежными в графе и каждый путь из одной ветви
в другую обязательно проходит через вершину
в дереве. Так как поперечных ребер нет, то вершины из
разных ветвей не могут быть смежными в графе и каждый путь из одной ветви
в другую обязательно проходит через вершину  . Следовательно,
если
степень вершины
. Следовательно,
если
степень вершины  в DFS-дереве больше 1, то эта вершина -
шарнир. Если же степень вершины
в DFS-дереве больше 1, то эта вершина -
шарнир. Если же степень вершины  в DFS-дереве равна 1, то
в дереве имеется единственная вершина
в DFS-дереве равна 1, то
в дереве имеется единственная вершина  , смежная
с
, смежная
с  ,
и каждая из остальных вершин графа соединена
с вершиной
,
и каждая из остальных вершин графа соединена
с вершиной  путем, не
проходящим через
путем, не
проходящим через  . Поэтому в данном случае удаление
вершины
. Поэтому в данном случае удаление
вершины  не нарушает связности графа и эта вершина не является шарниром.
не нарушает связности графа и эта вершина не является шарниром.
Это свойство корня DFS-дерева можно было бы использовать для выявления
всех шарниров, просто выполнив  раз поиск в глубину, стартуя
поочередно в каждой вершине. Оказывается, все шарниры можно выявить
однократным поиском в глубину. Следующая теорема характеризует все
шарниры, отличные от корня DFS-дерева. Напомним, что каждая вершина дерева
является и предком, и потомком самой себя. Предок (потомок) вершины,
отличный от самой этой вершины, называется собственным предком (потомком).
раз поиск в глубину, стартуя
поочередно в каждой вершине. Оказывается, все шарниры можно выявить
однократным поиском в глубину. Следующая теорема характеризует все
шарниры, отличные от корня DFS-дерева. Напомним, что каждая вершина дерева
является и предком, и потомком самой себя. Предок (потомок) вершины,
отличный от самой этой вершины, называется собственным предком (потомком).
Теорема 2. Пусть  - DFS-дерево графа
- DFS-дерево графа  с корнем
с корнем  .
Вершина
.
Вершина  является шарниром графа тогда
и только тогда, когда у нее в дереве
является шарниром графа тогда
и только тогда, когда у нее в дереве  имеется такой
сын
имеется такой
сын  , что ни один потомок вершины
, что ни один потомок вершины  не
соединен ребром ни с одним собственным предком вершины
не
соединен ребром ни с одним собственным предком вершины  .
.
Доказательство. Если  - сын вершины
- сын вершины  и ни один
потомок вершины
и ни один
потомок вершины  не соединен ребром ни с одним собственным
предком вершины
не соединен ребром ни с одним собственным
предком вершины  , то, ввиду отсутствия поперечных ребер, любой
путь, соединяющий вершину
, то, ввиду отсутствия поперечных ребер, любой
путь, соединяющий вершину  с корнем, проходит
через
с корнем, проходит
через  .
Следовательно, в этом случае вершина
.
Следовательно, в этом случае вершина  - шарнир. Если же для
каждого сына
- шарнир. Если же для
каждого сына  вершины
вершины  имеется ребро, соединяющее
вершину
имеется ребро, соединяющее
вершину  с каким-либо собственным предком
вершины
с каким-либо собственным предком
вершины  , то
каждый сын вершины
, то
каждый сын вершины  соединен с корнем дерева путем, не
проходящим
через
соединен с корнем дерева путем, не
проходящим
через  . Поэтому при удалении вершины
. Поэтому при удалении вершины  граф
останется связным и
граф
останется связным и  в этом случае не является шарниром.
в этом случае не является шарниром.
Для применения этого критерия к поиску шарниров введем на множестве вершин
функцию  , связанную с DFS-деревом: значением
, связанную с DFS-деревом: значением  является наименьший из глубинных номеров вершин, смежных с потомками
вершины
является наименьший из глубинных номеров вершин, смежных с потомками
вершины  . Если вершина
. Если вершина  является сыном
вершины
является сыном
вершины  ,
то
,
то 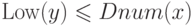 (так как вершина
(так как вершина  является
потомком
самой себя и смежна с вершиной
является
потомком
самой себя и смежна с вершиной  ). Из теоремы 2 следует, что
вершина
). Из теоремы 2 следует, что
вершина  , отличная от
, отличная от  , является шарниром тогда
и только
тогда, когда у нее имеется сын
, является шарниром тогда
и только
тогда, когда у нее имеется сын  такой, что
такой, что 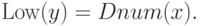
Функцию  можно определить рекурсивно - если мы
знаем ее
значения для всех сыновей вершины
можно определить рекурсивно - если мы
знаем ее
значения для всех сыновей вершины  и глубинные номера всех
вершин, смежных с
и глубинные номера всех
вершин, смежных с  и не являющихся ее сыновьями, то
и не являющихся ее сыновьями, то  есть минимум из всех этих величин, то есть
есть минимум из всех этих величин, то есть
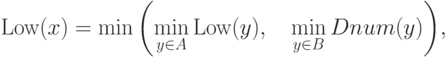
где  обозначает множество всех сыновей вершины
обозначает множество всех сыновей вершины  ,
а
,
а  - множество всех остальных вершин, смежных
с
- множество всех остальных вершин, смежных
с  . Нетрудно
видеть, что это определение эквивалентно первоначальному. Исходя из него,
можно вычислять значения функции
. Нетрудно
видеть, что это определение эквивалентно первоначальному. Исходя из него,
можно вычислять значения функции  в процессе поиска в
глубину
с помощью следующей рекурсивной процедуры. Предполагается, что вначале всем
элементам массива
в процессе поиска в
глубину
с помощью следующей рекурсивной процедуры. Предполагается, что вначале всем
элементам массива 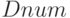 присвоены нулевые значения.
присвоены нулевые значения.
Procedure 
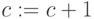
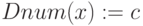
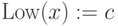
-
for
 do
do
-
if
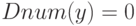
-
then ComputeLow(
 )
) 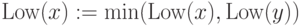
-
else

