Реляционная модель данных
Операции над отношениями. Реляционная алгебра
Напомним, что алгеброй называется множество объектов с заданной на нем совокупностью операций, замкнутых относительно этого множества, называемого основным множеством.
Основным множеством в реляционной алгебре является множество отношений. Всего Э. Ф. Коддом было предложено 8 операций. В общем это множество избыточное, так как одни операции могут быть представлены через другие, однако множество операций выбрано из соображений максимального удобства при реализации произвольных запросов к БД. Все множество операций можно разделить на две группы: теоретико-множественные операции и специальные операции. В первую группу входят 4 операции. Три первые теоретико-множественные операции являются бинарными, то есть в них участвуют два отношения и они требуют эквивалентных схем исходных отношений.
Теоретико-множественные операции реляционной алгебры
Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно.
Пусть заданы два отношения R1 = { r1 } , R2 = { r2}, где r1 и r2 - соответственно кортежи отношений R1 и R2, то объединение
 .
.
Здесь r — кортеж нового отношения,  — операция логического сложения "ИЛИ".
— операция логического сложения "ИЛИ".
Пример применения операции объединения приведен на рис. 4.1. Исходными отношениями являются отношения R1 и R2, которые содержат перечни деталей, изготавливаемых соответственно на первом и втором участках цеха. Отношение R3 содержит общий перечень деталей, изготавливаемых в цеху, то есть характеризует общую номенклатуру цеха.
| R1 | |
|---|---|
| Шифр детали | Название детали |
| 00011073 | Гайка M1 |
| 00011075 | Гайка М2 |
| 00011076 | Гайка М3 |
| 00011003 | Болт М1 |
| 00011006 | Болт М3 |
| 00013063 | Шайба М1 |
| 00013066 | Шайба М3 |
| R2 | |
|---|---|
| Шифр детали | Название детали |
| 00011073 | Гайка M1 |
| 00011076 | Гайка М3 |
| 00011077 | Гайка М4 |
| 00011004 | Болт М2 |
| R3 | |
|---|---|
| Шифр детали | Название детали |
| 00011073 | Гайка M1 |
| 00011075 | Гайка М2 |
| 00011076 | Гайка М3 |
| 00011003 | Болт М1 |
| 00011006 | Болт М3 |
| 00013063 | Шайба М1 |
| 00013066 | Шайба М3 |
| 00011077 | Гайка М4 |
| 00011004 | Болт М2 |
Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям. R1 и R2:

здесь  — операция логического умножения (логическое "И").
— операция логического умножения (логическое "И").
В отношении R4 содержатся перечень деталей, которые выпускаются одновременно на двух участках цеха.
Разностью отношений R1 и R2 называется отношение, содержащее множество кортежей, принадлежащих R1 и не принадлежащих R2:

Отношение R5 содержит перечень деталей, изготавливаемых только на участке 1, отношение R6 содержит перечень деталей, изготавливаемых только на участке 2.
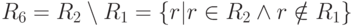
| R5 | |
|---|---|
| Шифр детали | Название детали |
| 00011075 | Гайка М2 |
| 00011003 | Болт М1 |
| 00013063 | Шайба М1 |
| 00013066 | Шайба М3 |
Следует отметить, что первые две операции, объединение и пересечение, являются коммутативными операциями, то есть результат операции не зависит от порядка аргументов в операции. Операция же разности является принципиально несимметричной операцией, то есть результат операции будет различным для разного порядка аргументов, что и видно из сравнения отношений R5 и R6.
В отличие от навигационных средств манипулирования данными в теоретико-графовых моделях операции реляционной алгебры позволяют получить сразу иной качественный результат, который является семантически гораздо более ценным и понятным пользователям. Например, сравнение результатов объединения и разности номенклатуры двух участков позволит оценить специфику производства: насколько оно уникально на каждом участке, и, в зависимости от необходимости, принять соответствующее решение по изменению номенклатуры.
Для демонстрации возможностей трех первых операций реляционной алгебры рассмотрим еще один пример — уже из другой предметной области. Исходными являются три отношения R1 R2 и R3. Все они имеют эквивалентные схемы.
- R1= (ФИО, Паспорт, Школа) ;
- R2= (ФИО, Паспорт, Школа) ;
- R3= (ФИО, Паспорт, Школа).
Рассмотрим ситуацию поступления в высшие учебные заведения, которая была характерна для периода, когда были разрешены так называемые репетиционные вступительные экзамены, которые сдавались раньше основных вступительных экзаменов в вуз. Отношение R1 содержит список абитуриентов, сдававших репетиционные экзамены. Отношение R2 содержит список абитуриентов, сдававших экзамены на общих условиях. И наконец, отношение R3 содержит список абитуриентов, принятых в институт. Будем считать, что при неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке, поэтому некоторые абитуриенты могут присутствовать как в первом, так и во втором отношении.
Ответим на следующие вопросы:
- Список абитуриентов, которые поступали два раза и не поступили в вуз.
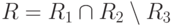
- Список абитуриентов, которые поступили в вуз с первого раза, то есть они сдавали экзамены только один раз и сдали их так хорошо, что сразу были зачислены в вуз.

- Список абитуриентов, которые поступили в вуз только со второго раза.
Прежде всего это те абитуриенты, которые присутствуют в отношениях R1 и R2, потому что они поступали два раза, и присутствуют в отношении R3, потому что они поступили.

- Список абитуриентов, которые поступали только один раз и не поступили.
Это прежде всего те абитуриенты, которые присутствуют в R1 и не присутствуют в R2, и те, кто присутствуют в R2 и не присутствуют в R1. И разумеется, никто из них не присутствует в R3.

В отсутствие скобок порядок выполнения операций реляционной алгебры естественный, поэтому сначала будут выполнены операции в скобках, а затем будет выполнена последняя операция вычитания отношения R3.
Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.
Кроме трех перечисленных операций в рамках реляционной алгебры определена еще одна теоретико-множественная операция — расширенное декартово произведение. Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения, обозначаемая  , допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
, допустима для любых двух отношений. Но прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.
Сцеплением,или конкатенацией,кортежей c = <c1, c2, ..., cn> и q = <q1, q2, ..., qm> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей c и q обозначается как (c , q).
(c, q) = <c1, c2, ... , cn, q1, q2, ..., qm>
Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q.
Все предыдущие операции не меняли степени или арности отношений — это следует из определения эквивалентности схем отношений. Операция декартова произведения меняет степень результирующего отношения.
Расширенным декартовым произведением отношения R1 степени n со схемой
SR1 = (A1, A2, ... , An),
и отношения R2 степени m со схемой
SR2 = (B1, B2, ..., Bm),
называется отношение R3 степени n+m со схемой
SR3 = (A1, A2, ... , An, B1, B2, ..., Bm),
содержащее кортежи, полученные сцеплением каждого кортежа r отношения R1 с каждым кортежем q отношения R2.
То есть если R1 = { r }, R2 = { q }
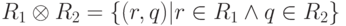
Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной. Очень часто операция расширенного декартова произведения используется для получения некоторого универсума — т. е. отношения, которое характеризует все возможные комбинации между элементами отдельных множеств. Однако самостоятельного значения результат выполнения операции обычно не имеет, он участвует в дальнейшей обработке. Например, на производстве в отношении R7 задана обязательная номенклатура деталей для всех цехов, а в отношении R8 дан перечень всех цехов.
| R7 | |
|---|---|
| Шифр детали | Название детали |
| 00011073 | Гайка M1 |
| 00011075 | Гайка М2 |
| 00011076 | Гайка М3 |
| 00011003 | Болт М1 |
| 00011006 | Болт М3 |
| 00013063 | Шайба М1 |
| 00013066 | Шайба М3 |
| 00011077 | Гайка М4 |
| 00011004 | Болт М2 |
| 00011005 | Болт М5 |
| 00011006 | Болт М6 |
| 00013062 | Шайба М2 |
Тогда отношение R9, которое соответствует ситуации, когда каждый цех изготавливает все требуемые детали, будет выглядеть следующим образом:
| R9 | ||
|---|---|---|
| Шифр детали | Название детали | Цех |
| 00011073 | Гайка M1 | Цех 1 |
| 00011075 | Гайка М2 | Цех 1 |
| 00011076 | Гайка М3 | Цех 1 |
| 00011003 | Болт М1 | Цех 1 |
| 00011006 | Болт М3 | Цех 1 |
| 00013063 | Шайба М1 | Цех 1 |
| 00013066 | Шайба М3 | Цех 1 |
| 00011077 | Гайка М4 | Цех 1 |
| 00011004 | Болт М2 | Цех 1 |
| 00011005 | Болт М5 | Цех 1 |
| 00011006 | Болт М6 | Цех 1 |
| 00013062 | Шайба М2 | Цех 1 |
| 00011073 | Гайка M1 | Цех 2 |
| 00011075 | Гайка М2 | Цех 2 |
| 00011076 | Гайка М3 | Цех 2 |
| 00011003 | Болт М1 | Цех 2 |
| 00011006 | Болт М3 | Цех 2 |
| 00013063 | Шайба М1 | Цех 2 |
| 00013066 | Шайба М3 | Цех 2 |
| 00011077 | Гайка М4 | Цех 2 |
| 00011004 | Болт М2 | Цех 2 |
| 00011005 | Болт М5 | Цех 2 |
| 00011006 | Болт М6 | Цех 2 |
| 00013062 | Шайба М2 | Цех 2 |
| 00011073 | Гайка M1 | Цех 3 |
| 00011075 | Гайка М2 | Цех 3 |
| 00011076 | Гайка М3 | Цех 3 |
| 00011003 | Болт М1 | Цех 3 |
| 00011006 | Болт М3 | Цех 3 |
| 00013063 | Шайба М1 | Цех 3 |
| 00013066 | Шайба М3 | Цех 3 |
| 00011077 | Гайка М4 | Цех 3 |
| 00011004 | Болт М2 | Цех 3 |
| 00011005 | Болт М5 | Цех 3 |
| 00011006 | Болт М6 | Цех 3 |
| 00013062 | Шайба М2 | Цех 3 |
| R10 | ||
|---|---|---|
| Шифр детали | Название детали | Цех |
| 00011073 | Гайка M1 | Цех 1 |
| 00011075 | Гайка М2 | Цех 1 |
| 00011076 | Гайка М3 | Цех 1 |
| 00011003 | Болт М1 | Цех 1 |
| 00011006 | Болт М3 | Цех 1 |
| 00013063 | Шайба М1 | Цех 1 |
| 00013066 | Шайба М3 | Цех 1 |
| 00011077 | Гайка М4 | Цех 1 |
| 00011004 | Болт М2 | Цех 1 |
| 00011006 | Болт М3 | Цех 2 |
| 00013063 | Шайба М1 | Цех 2 |
| 00013066 | Шайба М3 | Цех 2 |
| 00011077 | Гайка М4 | Цех 2 |
| 00011004 | Болт М2 | Цех 2 |
| 00011006 | Болт М6 | Цех 2 |
| 00013062 | Шайба М2 | Цех 2 |
| 00011073 | Гайка M1 | Цех 3 |
| 00011075 | Гайка М2 | Цех 3 |
| 00011076 | Гайка М3 | Цех 3 |
| 00011003 | Болт М1 | Цех 3 |
| 00011006 | Болт М3 | Цех 3 |
| 00013063 | Шайба М1 | Цех 3 |
| 00013066 | Шайба М3 | Цех 3 |
| 00011077 | Гайка М4 | Цех 3 |
| 00011005 | Болт М5 | Цех 3 |
| 00011006 | Болт М6 | Цех 3 |
| 00011005 | Болт М5 | Цех 1 |
| 00011006 | Болт М6 | Цех 1 |
| 00013062 | Шайба М2 | Цех 1 |
В каких запросах нужно использовать расширенное декартово произведение? Эта операция моделирует некоторую ситуацию, которая характеризуется словом "все". Поэтому если нам надо узнать, какие детали в каких цехах из общей обязательной номенклатуры не выпускаются, то мы можем вычесть из полученного отношения R9 отношение R10, характеризующее реальный выпуск деталей в каждом цехе.
Отношение R11, которое является результатом выполнения этой операции, имеет вид:
R11 =R9 \R10
| R11 | ||
|---|---|---|
| Шифр детали | Название детали | Цех |
| 00011073 | Гайка M1 | Цех 2 |
| 00011075 | Гайка М2 | Цех 2 |
| 00011076 | Гайка М3 | Цех 2 |
| 00011004 | Болт М2 | Цех 3 |
| 00013062 | Шайба М2 | Цех 3 |
| 00011003 | Болт М1 | Цех 2 |
| 00011005 | Болт М5 | Цех 3 |
Группа теоретико-множественных операций избыточна, так, например, операцию пересечения можно заменить сочетанием операций объединения и разности.

Однако это достаточно сложная формула, и именно поэтому все три теоретико-множественные операции вошли в базовый набор операций реляционной алгебры.
Далее мы переходим к группе операций, названных специальными операциями реляционной алгебры.
