Характеристические числа графов и их применение в конструкторском проектировании РЭС

Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.

Рассмотрим некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа. К таким числам, не зависящим от изоморфных преобразований, относятся: цикломатическое \[ v(G) \] и хроматическое \[ k(G) \] числа, числа внутренней \[ \alpha(G) \] и внешней \[ \beta(G) \] устойчивости графа.

18. 1. Цикломатическое число

При рассмотрении произвольного неориентированного графа \[ G(X, U) \] без петель с \[ X | = n \] и \[ U = r \] , состоящего из " \[ р \] " компонент связности, величину

\[ v(G) = r - n + p \]

называют цикломатическим числом графа.

Иногда вводят понятие ранга графа

\[ R(G) = n-p. \]

В этом случае цикломатическое число

\[ v(G) = r-R(G). \]

Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.

Цикломатическое число всегда неотрицательно.

Основное свойство цикломатического числа формулируется в виде теоремы:

Цикломатическое число мультиграфа равно максимальному числу независимых циклов.

Знание цикломатического числа оказывается полезным при анализе топологии электронных схем, а также для решения целого класса задач конструкторского проектирования РЭС.

Пример. Если рассматривать конструкцию печатной платы, то схему электрических соединений можно интерпретировать графом \[ G (X, U) \] , где \[ X \] - множество областей контактных площадок, внутри которых проведение проводников запрещено, a \[ U \] - множество трасс.

При этом всё коммутационное пространство разбивается проведёнными соединениями на отдельные, локально замкнутые области

\[ Q = {q_{1} , q_{2 }, ...,q_{g}}. \]

Любые две вершины \[ х_{i }, x_{j} \in X, \] находящиеся в различных областях \[ q_{s} , q_{i} \in Q \] , не могут быть соединены ребром \[ u_{k} \in U \] без пересечения рёбер (соединений), ограничивающих области \[ q_{s} \] и \[ q _{t } \] .

В связи с этим возникает необходимость контроля непопадания смежных вершин в различные изолированные области.

Цикломатическое число \[ v (G) \] позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа \[ G (X, U) \] .

18. 2. Хроматическое число

Пусть, задан граф \[ G (X, U) \] без петель. Разобьём множество его вершин на k непересекающихся подмножеств

\[ X_{1}, X_{2}, … , X_{k}, X =\bigcup\limits_{i=1}^k{X_i}, \forall X_{i}, X_{j} \subset X; [X_{i}\cap X_{j}=\varnothing] \]

так, чтобы любые две смежные вершины \[ x_{s} , x_{t} \in X \] принадлежали разным подмножествам, т.е. чтобы рёбра графа \[ G (X, U) \] соединяли вершины из разных подмножеств

\[ \forall X_s \in X[X_s\in X_i \Leftarrow ГX_s \not\subset X_i] \]

Отметим все вершины \[ x \] индексами \[ 1,2, ... , k \] (т.е. раскрасим вершины \[ k \] цветами), причём вершины внутри каждого подмножества \[ X_{j} \] помечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы.

Наименьшее возможное число подмножеств, получаемое в результате такого разбиения вершин графа \[ G (X, U) \] , называют хроматическим числом графа \[ k (G) \] , граф \[ G (X, U) \] называют \[ k \] - хроматическим,а выражения (18.5) и (18.6)- хроматическим разложением \[ X \] .

Особое значение имеет частный вид \[ k \] - хроматического графа - бихроматический или двудольный граф, для которого множество вершин \[ X \] можно разбить на два непересекающихся подмножества \[ X_{1} \] и \[ Х_{2} \] так, чтобы никакое ребро не соединяло бы вершины одного и того же подмножества, т.е.

\[ X = X_{1}\cup X_{2}, X_{1}\cap X_{2}; \] \[ \forall x_{i} , x_{j}\in X [(x_{i} , x_{j}) = u_{f }\in U \Leftarrow (x_{i}\in X_{1 }& x_{j}\in X_{2})\cup (x_{i}\in X_{2} & x_{j}\in X_{1})]. \]

Такие графы называют графами Кёнига и обозначают \[ G(X_{1},X_{2},U) \] .

Критерий бихроматичности произвольного графа формулируется теоремой Кёнига, согласно которой обыкновенный граф \[ G (X, U) \] является бихроматическим тогда и только тогда, когда он не содержит циклов нечётной длины.

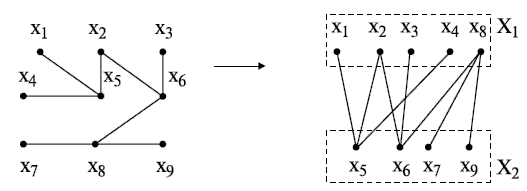
Если граф \[ G (X, U) \] - дерево, т.е. в нём полностью отсутствуют циклы (существуют лишь циклы нулевой длины), то он является бихроматическим графом и может быть представлен в виде двудольного графа (рис. 18.1).

Граф Кёнига \[ G (X_{1}, Х_{2}, U) \] называют полным, если каждая вершина \[ x_{i} \in X_{1} \] смежна с каждой вершиной \[ x_{j} \in X_{2}, \] и наоборот.

Пример. Рассмотрим пример бихроматического графа \[ G (X_{1}, X_{2}, U) \] , у которого

При добавлении к этому графу рёбер \[ (х_{2} x_{6}) \] , \[ (х_{2} x_{8}) \] , \[ (х_{3} x_{5}) \] , \[ (х_{3} x_{7}) \] и \[ (х_{4} х_{5}) \] получим полный бихроматический граф. Очевидно, что подмножество \[ X_{1} \] множества вершин \[ X \] можно раскрасить в один цвет, а \[ Х_{2} \] - в другой.

Число рёбер полного бихроматического графа \[ G (X_{1} , Х_{2}, U) \]

\[ r = U = x_{1} x_{2} . \]

При составлении целого ряда алгоритмов проектирования РЭС используют операцию удаления некоторых вершин и рёбер графа. При этом особое значение приобретает понятие критического графа.

Граф \[ G (X, U) \] называют критическим, если удаление любой вершины \[ x_{i} \in X \] с инцидентными ей рёбрами уменьшает хроматическое число графа.

Критическим \[ 1 \] - хроматическим графом является одна вершина; критическим 2 - хроматическим - две вершины, соединённые ребром; критическим \[ 3 \] - хроматическим - простой цикл нечётной длины, так как при удалении из него любой вершины с инцидентными ей рёбрами получим двудольный граф. Очевидно, что полный граф всегда является критическим, причём его хроматическое число равно

\[ k(G) = X = n . \]

В отличие от цикломатического числа определение хроматического числа осуществляется с помощью сравнительно сложных алгоритмов, в основу большинства которых положены методы целочисленного линейного программирования.

Оценка хроматического числа через число вершин графа \[ G (X, U) \] имеет вид:

\[ 1 \le k(G) \le X = n . \]

В этом выражении нижняя граница соответствует пустым, а верхняя - полным графам.

На практике для простых связных графов оценить величину \[ k (G) \] можно следующим образом.

Сначала выбираем вершину с минимальной локальной степенью и пометим (раскрасим) её, затем произведём хроматическую раскраску вершин, смежных с данной, и так далее.

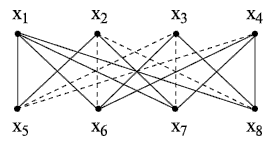
Например, для графа на рис. 18.2, б сначала выбираем вершину \[ х_{3}, \] для которой \[ \rho (х_{3}) = 1 \] , и раскрасим её в красный цвет. Тогда вершину \[ х_{2} \] можно раскрасить в синий цвет, а вершины \[ х_{1} \] и \[ x_{5} \] - в красный (они не смежны с \[ х_{3} \] ). Вершины \[ х_{6} \] и \[ х_{8} \] можно раскрасить в синий цвет, а оставшиеся вершины \[ х_{4} , x_{7} и x_{9} \] - в жёлтый. На раскраску вершин графа пошло три краски \[ k (G) = 3 \] .

Знание хроматического числа графа позволяет в ряде случаев упростить алгоритмы, используемые на этапе конструкторского проектирования РЭС.

Пример. Рассмотрим задачу оценки числа слоёв многослойной печатной платы. Пусть, граф \[ G (X, U) \] интерпретирует фрагмент коммутационного поля платы, где х - множество областей контактных площадок конструктивных элементов, внутри которых проведение проводников запрещено, a \[ U \] - множество трасс платы.

Построим граф пересечений \[ Q (Y, V) \] , в котором вершинами являются отдельные компоненты связности (электрические цепи) графа \[ G (X, U) \] , причём \[ у_{i}, y_{j} \in Y \] смежны, если соответствующие им компоненты связности \[ G_{i} (X_{i }, U_{i}) \] и \[ G_{j} (X_{j }, U_{j}) \] перекрывают друг друга.

При этом хроматическое число \[ k (Q) \] графа \[ Q (Y, V) \] определит верхнюю границу числа коммутационных слоев рассматриваемого фрагмента платы (в нашем примере \[ k (Q) = 2 \] ). В этом случае цепи, соответствующие вершинам одного цвета графа \[ Q (Y, V) \] , можно располагать в одном слое печатной платы.