Упражнения

Это приложение содержит задачи, которые даются на тестовых экзаменах в Датском Техническом Университете.

Предполагается, что настоящее русское издание в Интернете будет содержать Интернет-версию этих тестовых задач, представленную для автоматического тестирования с помощью системы альтернативных вопросов, где будет более подробно рассмотрен процесс решения.

Упражнение 2.1. Предложенная нагрузка

1. Рассмотрим Интернет-кафе. Клиенты прибывают случайно, в среднем 20 клиентов в час. Среднее время использования терминала -15 минут.

   Вопрос. 1.1: Найдите предложенную нагрузку, измеренную в единицах среднего времени обслуживания в течение одного часа.

   Вопрос. 1.2: Найдите предложенную нагрузку, измеренную в Эрлангах.

2. Рассмотрим ячейку в сотовой системе связи. Есть два процесса поступления вызовов.

   • Хендовер (передача соединения) происходит со скоростью 3 вызова в минуту, и среднее время пребывания в системе 90 секунд.
   • Новые вызовы прибывают со скоростью 240 вызовов в час, и среднее время пребывания в системе - 2 минуты.

   Вопрос. 2.1: Найдите предложенную нагрузку для каждого потока нагрузки и полную предложенную нагрузку в Эрлангах.

3. К компьютерной системе поступают три типа задач:

   • диалоговые задачи,
   • испытательные задачи,
   • производительные задачи.

   Все задачи прибывают согласно Пуассоновскому процессу, и времена обслуживания являются постоянными.

   Интенсивность поступления задач следующая:

   • 15 задач прибывают в минуту, и время обслуживания - 1с.
   • 3 задачи прибывают в минуту, и время обслуживания - 5 с.
   • 12 задач прибывают в час, и время обслуживания - 2 минуты.

   Вопрос. 3.1: Найдите предложенную нагрузку для каждого типа и полную предложенную нагрузку.

4. Процесс поступления вызовов к системам возникает согласно Пуассоновскому процессу со скоростью \[ \lambda = 2 \] вызовов в единицу времени. Каждый вызов занимает два канала в течение целого времени занятия, которое является экспоненциально распределенным со средней величиной \[ s = 3 \] единицы времени.

   Вопрос. 4.1: Найдите предложенную нагрузку на вызовах (подключения).

   Вопрос. 4.2: Найдите предложенную нагрузку в каналах.

5. Мы рассматриваем нагрузку к цифровой станции, содержащую вызовы цифровой сети интегрального обслуживания (1 вызов на канал) и цифровой сети интегрального обслуживания с 2 вызовами (2 вызова на канал).

   • Вызовы цифровой сети интегрального обслуживания: прибывают 900 вызовов в час и среднее время пребывания в системе - 2 минуты.
   • Цифровая сеть интегрального обслуживания - 2 вызова: прибывают 2 вызова в минуту и среднее время их пребывания в системе - 150 секунд.

   Вопрос. 5.1: Найдите предложенную нагрузку (измеренную в каналах) для каждого типа и общее количество предложенной нагрузки.

6. Цифровые линия связи 2.048 Мгб/с в среднем принимают 128 пакетов в секунду. Пакет содержит в среднем 1500 байтов (1 байт = 8 битов).

   Вопрос. 6.1: Найдите использование \[ \xi \] , линии связи.

Упражнение 7.1. В-формула Эрланга

В торговом центре есть игровой зал. Посетители решают, случайно и независимо друг от друга, войти и поиграть, но если все игровые машины заняты, то они переходят в другое место (как альтернатива имеется Интернет-кафе).

В течение часов работы в среднем входят, чтобы поиграть, 40 человек в час.

Люди выбирают первую от входа свободную машину и играют в среднем по 6 минут (экспоненциально распределенных). Игровая машина имеет в среднем доход, равный 100 эре в минуту, если она используется. Полные расходы за арендную плату комнат и обслуживания на одну машину - 20 крон в час, независимо от того, используется она или нет. По В-формуле Эрланга можно вычислить, используя рекурсивную формулу, таблицы или компьютеры:

1. Предложенную нагрузку.
2. Каков доход нетто, когда число машин - 4?

3. Выгодно ли иметь машин больше или меньше, чем 4?

   Каково оптимальное число машин?

   Далее мы предполагаем, что число машин - 4.
4. Сколько монет владелец может ожидать от каждой машины после 12 часов открытия?
5. Какое время пройдет, пока последний клиент уйдет после закрытия, если есть 1,2,3 или 4 человека, играющие в заключительное время?
6. Каково соотношение времени, когда только одна машина (случайная) свободна?
7. какова вероятность, что свободна машина, находящаяся дальше всего от входа?

Упражнение 7.7. Модель ALOHA

Определение метода случайного доступа ALOHA см. в примере 6.2.2.

Мы рассматриваем систему \[ М/G/l \] , куда сообщения прибывают согласно Пуассоновскому процессу с интенсивностью (скоростью) \[ \lambda \] , а распределение времени пребывания в системе дается \[ F(t) \] со средней величиной \[ s=1 \] .

Есть бесконечное число обслуживающих приборов, и вероятности состояний системы зависят только от распределения времени пребывания в системе через среднюю величину (нечувствительность).

1. Найти предложенную нагрузку и вероятности состояния согласно предположению о статистическом равновесии.

   Сообщение обслуживается правильно, только если является единственным в течение всего времени пребывания в системе. Таким образом, система должна быть пуста во время прибытия, и ни один новый вызов не может поступить в течение времени пребывания в системе предыдущего вызова.

   В следующих двух вопросах мы принимаем, что время пребывания в системе является постоянным со средней величиной

   \[ s=1 \] .
2. Найти вероятность, что сообщение передано правильно.

3. Найти нагрузку, которая будет обслужена правильно, и показать, что она имеет максимум, равный \[ 1/2е= 0,1839 \] для \[ \lambda = 0,5 \] .

   В остающейся части упражнения примем, что время пребывания в системе является экспоненциально распределенным со средней величиной \[ s= 1 \] .
4. Найти вероятность, что сообщение передано правильно.
5. Показать, что общее количество правильно переданных в единицу времени сообщений имеет максимум (0.2059) для \[ \lambda= (\sqrt 5 -1)/2=0,6180 \] .
6. Найти функцию распределения и среднюю величину времени пребывания в системе сообщений, которые переданы правильно. Затем найти обслуженную нагрузку сообщений, которые переданы правильно.

Упражнение 7.8. Прибытие пакетов в систему с потерями

Мы рассматриваем чистую систему с потерями с 4 каналами. События возникают в процессе поступления вызовов согласно Пуассоновскому процессу с интенсивностью \[ \lambda =1 [\mbox{события/единица времени}] \] . Каждое событие соответствует двум попыткам вызова, которые обслуживаются независимо. Если в момент прибытия есть только один свободный канал, то одна из этих двух случайных попыток вызова будет отклонена. Время обслуживания - экспоненциально распределенное со средней величиной

\[ \mu^{-1} = 1 [\mbox{единица времени}] \]

1. Найти предложенную нагрузку (измеренную в каналах).
2. Установить диаграмму переходов состояний системы, когда состояние х определяется как общее количество занятых каналов (х = 0, 1,2,3,4)-

3. Показать, что вероятности состояний согласно предположению о статистическом равновесии будут:

   \[ \left \{ \frac{12}{49}, \frac{12}{49}, \frac{12}{49}, \frac{8}{49}, \frac{5}{49} \right \} \]

   Найдите потери по нагрузке (соотношение предложенной и потерянной нагрузок).
4. Найти потери системы по времени и по вызовам.

Упражнение 7.9. Эрланговская система с потерями

Мы рассматриваем систему с потерями Эрланга с \[ n = 3 \] обслуживающими приборами. Процесс поступления вызовов - Пуассоновский процесс с интенсивностью \[ \lambda = 0,5 \] в единицу времени вызова. Время обслуживания является экспоненциально распределенным со средней величиной 4 единицы времени.

1. Найти предложенную нагрузку \[ А \] .
2. Создать диаграмму переходов состояний и найти вероятности состояния, когда система находится в статистическом равновесии.
3. Получить дифференциальные уравнения, которые описывают систему (только для состояния 2).
4. Найти вероятность блокировки \[ Е \] , применяя рекурсивную формулу для В-формулы Эрланга (отдельные рекурсии должны получиться из ответа).
5. Найти согласно предположению о последовательном поиске нагрузку, которую несет отдельный обслуживающий прибор.
6. Показать, что вероятности состояния системы, наблюдаемой вызовом (клиентом), покидая систему (обратным подсчетом), такие же, как те, что наблюдаются клиентом в момент, когда он входит в систему (учитывая блокированных клиентов). Используйте диаграмму переходов состояний, чтобы найти, сколько клиентов прибывают/ покидают систему в каждом состоянии.

Упражнение 7.10. Эрланговская система с потерями

Мы рассматриваем систему с потерями, которая имеет 4 канала и обслуживает РСТ-1 нагрузку. Интенсивность поступления (интенсивность) \[ \lambda - 1 \] вызов в единицу времени, и среднее время обслуживания \[ \mu^{-1} - 2 \] единицы времени. Система предположительно находится в статистическом равновесии.

1. Найти предложенную нагрузку и нарисовать диаграмму переходов состояний системы.
2. Найти вероятности состояния и потери по времени, потери по вызовам, потери по нагрузке.
3. Вычислить потери по времени, используя рекурсивную формулу для В-формулы Эрланга. Отдельные шаги рекурсий должны быть приведены.
4. Принять, что порядок поиска случайный, и найти вероятность, что два заданных канала являются занятыми (остающиеся каналы могут быть заняты или свободны).
5. В каком количестве каналов мы нуждаемся, если нагрузка увеличится и примет значение 0,20? (Примените результаты, полученные в ответе на вопрос 1).
6. Найти распределение числа вызовов, которые будут потеряны в течение периода, когда все 4 канала заняты.

Упражнение 8.3. Система с потерями М/Е2/2

Рассмотрим систему с потерями с двумя каналами (обслуживающие приборы). Попытки вызова прибывают согласно Пуассоновскому процессу интенсивностью \[ \lambda \] вызовов в единицу времени. Время обслуживания \[ \lambda \] распределено в соответствии с Эрланговским распределением с интенсивностью \[ 2 \mu \] в каждой из этих двух фаз.

1. Найти предложенную нагрузку.

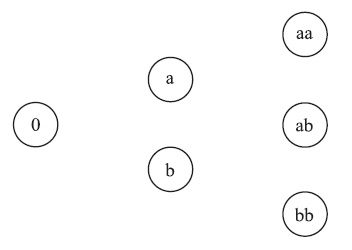
2. Создать диаграмму переходов состояний системы, где состояние обозначает число вызовов в системе и фазы вызовов. Примените следующее состояния, где \[ а \] и \[ b \] обозначают эти две фазы.

   

   
   
3. Найти согласно предположению о статистическом равновесии вероятности состояний системы, используя тот факт, что усеченное Пуассоновское распределение для данного среднего времени пребывания в системе справедливо для любого распределения времени обслуживания (свойство нечувствительности).
4. Блокирующее состояние "оба канала заняты" инициируется из состояния \[ а \] или \[ b \] . Определите для обоих из этих случаев распределение Кокса и продолжительности блокирующего состояния, применяя графическое представление распределения Кокса (диаграмму состояний).
5. Записать, преобразования Лапласа из распределения продолжительности периодов, когда оба канала заняты.
6. Найти среднюю величину и дисперсию числа попыток вызова, которые блокированы в течение периода, когда оба канала \[ а \] и \[ b \] заняты.

Упражнение 8.9. Энегсетовская система с потерями

Мы рассматриваем Энгсетовскую систему с потерями с 3 серверами, у которых предложенная нагрузка производится из 4 однородных источников. Свободный источник генерирует вызовы с интенсивностью \[ \lambda = 1/2 [\mbox{вызов/единица времени}] \] , и время обслуживания является экспоненциально распределенным со средней величиной \[ \mu^{-1} = 1 [\mbox{единица времени}] \] .

1. Найти полную предложенную нагрузку от этих 4 источников.
2. Установить диаграмму переходов состояний и найти вероятности состояния согласно предположению о статистическом равновесии.
3. Найти потери по времени, потери по вызовам и потери по нагрузке, используя следствия вопросов 1 и 2.
4. Найти распределение (плотность распределения) числа вызовов, которые блокированы в течение периода, когда все три сервера заняты.
5. Получить вероятности состояния системы свертыванием вероятности состояния 4 единственных источников и сделать сечение вероятности состояния в состоянии 3.

Упражнение 8.10. Система с потерями и интенсивностью прибытия, зависящей от состояния

Мы рассматриваем систему с потерями с \[ n = 2 \] каналами. Состояние системы \[ i \] определяется как число занятых каналов. Заявки от клиентов прибывают согласно Пуассоновскому процессу с интенсивностью, зависящей от состояния.

\[ \gamma(i)=\frac{3-i}{4-i}* \gamma[\mbox{заявок в единицу времени}], \quad 0 \le i \le 3. \]

Для всех других состояний \[ \gamma(i) = 0 \] .. Мы выбираем \[ \gamma = 1 \] заявки в единицу времени, а время обслуживания - экспоненциально распределенное с интенсивностью \[ \mu = 1 \] заявок в единицу времени.

1. Создать диаграмму переходов состояний системы.
2. Найти вероятности состояния системы согласно предположению о статистическом равновесии и определить потери по времени \[ Е \] .
3. Найти вероятности состояния \[ \pi(i) \] , как они выполняются при произвольном поступлении вызовов, и найти потери по вызовам \[ В \] .
4. Найти предложенную нагрузку, определенную как нагрузка, которая будет обслужена в системе без потерь, и найти потери по нагрузке \[ С \] .
5. Принять, что оба канала заняты. Какова вероятность, что следующее событие - попытка вызова (который, конечно, будет потерян)? Найти распределение числа вызовов, которые будут потеряны в течение периода занятости.
6. Дать вероятности состояния, как они замечены клиентом, который только что отбыл от системы. Мы включаем клиентов, которые блокированы.

Упражнение 8.11. Модель АЛОХАа с Энгсетовской нагрузкой

Мы рассматриваем Энгсетовскую модель с \[ S = 4 \] источниками. Среднее время пребывания в системе выбрано как единица времени ( \[ \mu^{-1} = 1 \] ). Интенсивность поступления свободного источника - \[ \gamma = 1/3 \] . Оба временных интервала являются экспоненциально распределенными. Число каналов бесконечно, то есть \[ п \le S \] . Состояние системы определено как число занятых каналов. Вышеупомянутая система - модель несинхронной системы АЛОХАа с \[ S \] передатчиками и экспоненциально распределенными длинами пакета.

1. Найти предложенную нагрузку \[ А \] .
2. Создать диаграмму переходов состояний и найти согласно предположению о статистическом равновесии вероятности состояния \[ p (i),(i = 0, l, \dots ,4) \] .
3. Найти вероятности состояния \[ \pi (i), (i = 0, 1, \dots , 4) \] , как они наблюдаются поступающим вызовом, перед поступлением (математические ожидания вызова). Используйте, как отправную точку, либо вероятности состояния, которые получены в вопросе 2, либо теорему прибытия.
4. Какова вероятность того, что вызов, прибывающий в нулевом состоянии (и, таким образом, изменяющий состояние из состояния нуль в состояние один), завершит обслуживание прежде, чем поступит следующий вызов? Это соответствует успешной передаче вызова в протоколе АЛОХАа.
5. Каково среднее время пребывания в системе успешно обслуженного вызова?