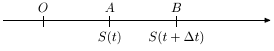Дифференцирование

Дифференцирование

Пусть задана функция y=f(x), \[ x\in D(f) \] , \[ y\in E(f) \] и точка \[ x_1=x+\Delta x\in D(f) \] , где \[ x\in D(f) \] . Тогда число \[ \Delta x=x_1-x \] называется приращением аргумента в точке x . Приращением функции \[ \Delta y \] в точке x соответствующего приращения \[ \Delta x \] называется число \[ \Delta y=y_1-y=f(x+\Delta x)-f(x) \] .

Рассмотрим несколько задач, которые привели к необходимости введения понятия производной функции.

Пример (Задача о движении). Некоторая точка движется по прямой по закону s=s(t), t - время (отсчитываемое от некоторой точки O ). Пусть в момент t=t₀ точка находилась в положении A, а при t=t₁ - в положении B (рис. 8.1).

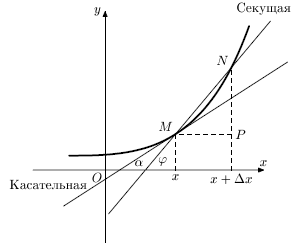
Тогда за время \[ \Delta t=t_1-t_0 \] точка прошла путь \[ |\overrightarrow{AB}|=s(t+\Delta t) - s(t)=\Delta s \] . Средняя скорость за промежуток времени \[ \Delta t \] равна \[ V _{\text{ср}} = \frac {s(t+\Delta t)-s(t)}{\Delta t} = \frac {\Delta s}{\Delta t}. \] Если движение равномерное, то \[ V_{\text{ср}}=const \] и этой характеристики достаточно для выяснения быстроты движения. Если же движение неравномерное, то \[ V_{\text{ср}}=V_{\text{ср}}(\Delta t)\ne const \] и поэтому вводится понятие мгновенной скорости прямолинейного движения (или скорость в данный момент времени \[ t \] ) как предельное значение средней скорости: \[ V_{\text{мгн}} = \lim\limits_{\Delta t\to 0} \frac {\Delta s}{\Delta t} = \lim\limits_{\Delta t\to 0} \frac {s(t+\Delta t)-s(t)}{\Delta t} \] (если этот предел существует и он конечен). Ясно, что \[ V_{\text{мгн}} = V_{\text{мгн}}(t) \] .

Пример (Задача о наклоне касательной к кривой). Пусть задана кривая y=f(x). Рассмотрим точки M(x; y) и \[ N(x+\Delta x; y+\Delta y) \] на этой кривой (рис. 8.2).

Касательной к линии y=f(x) в точке M называется прямая, которая совпадает с предельным значением прямой MN, когда точка N по кривой стремится к точке M, то есть \[ \Delta x\to 0 \] . Так как \[ \tg \varphi = \frac {|\overrightarrow{NP}|}{|\overrightarrow{MP}|} = \frac {\Delta y}{\Delta x} \] , то \[ \tg\varphi \to \tg\alpha \] или угловой коэффициент k касательной к кривой можно определять как \[ k=\tg\alpha = \lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x}. \]

Производной функции y=f(x) в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, при условии, что этот предел существует и конечен. Обозначают производную несколькими способами: y', f'(x), \[ \frac {dy}{dx} \] , \[ \frac {df}{dx} \] . Таким образом, \[ f'(x)=\lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x} = \lim\limits_{x\to 0} \frac {f(x+\Delta x)-f(x)}{\Delta x}. \]

Значение производной f'(x) при x=a (в точке x=a ) обозначается как: \[ y'(a), \ f'(a), \ y'|_{x=a},\ f'(x)|_{x=a} , \ \frac {dy}{dx} \bigl|_{x=a}. \]

Пример. Вычислим y', где \[ y=\sqrt{x} \] при x=1, используя только определение производной.

1. Находим \[ \Delta y=f(x+\Delta x)-f(x)=\sqrt{x+\Delta x}-\sqrt{x} \] ;
2. Находим предел: \[ \lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x} = \lim\limits_{\Delta x\to 0}\frac {\sqrt {x+\Delta x}-\sqrt{x}}{\Delta x} = \lim\limits_{\Delta x\to 0} \frac {1}{\sqrt{x+\Delta x}+\sqrt{x}} = \frac {1}{2\sqrt{x}} \ \implies \\ \implies \ (\sqrt{x})' = \frac {1}{2\sqrt{x}}; \]
3. Подставляя в это выражение x=1, находим \[ y'|_{x=1}=\frac {1}{2\sqrt{1}}=\frac 12 \] .

В задаче о наклоне касательной мы выяснили, что угловой коэффициент касательной в точке x, проведенной к кривой y=f(x), будет иметь вид \[ k=\lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x} \] . Поэтому \[ k=\tg\alpha =f'(x) \] .

Отсюда следует геометрический смысл производной в точке x: значение производной равно тангенсу угла, который образован касательной к графику функции y=f(x), проведенной в точке M(x; f(x)), с положительным направлением оси Ox . В задаче о движении мы выяснили, что \[ V_{\text{мгн}}=\lim\limits_{\Delta t\to 0}\frac {\Delta s}{\Delta t} \ \implies \ V_{\text{мгн}} =s'(t). \]

Отсюда следует механический смысл производной в точке x: значение производной равно мгновенной скорости (в момент времени x) материальной точки, движущейся по закону движения y=f(x) .

Найдем уравнение невертикальной касательной, проведенной к кривой y=f(x) в точке M₀(x₀;f(x₀)) (если касательная вертикальна, то f'(x) - не существует, так как при этом \[ \lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x}=\infty \] ). Так как ее угловой коэффициент k=f'(x₀), то уравнение касательной в точке M₀ будет иметь вид: y-f(x₀)=f'(x₀)(x-x₀).

Если у функции y=f(x) существует производная в точке x, то говорят, что функция y=f(x) дифференцируема в точке x.

Теорема(необходимое условие существования производной). Если функция y=f(x) дифференцируема в некоторой точке \[ x_0\in D(f) \] , то она в этой точке непрерывна. Обратное утверждение неверно, то есть непрерывность функции в точке x не является достаточным условием ее дифференцируемости в этой точке, и функция может быть непрерывной в точке, не имея в этой точке производной.

Теорема(правила дифференцирования функций). Если функции u=f(x) и v=g(x) дифференцируемы в некоторой точке из общей части их областей определения, иначе говоря, в точке \[ x\in D(f)\cap D(g) \] , то в этой точке дифференцируемы функции u+v, u-v, \[ u\cdot v \] , \[ \frac uv \] , причем справедливы, соответственно, формулы (дифференцирования суммы, разности, произведения и частного):

1. \[ (u\pm v)'=u'\pm v' \] ,
2. \[ (u\cdot v)' =u'v+uv' \] ,
3. \[ \Bigl(\frac uv\Bigr)' = \frac {u'v-v'u}{v^2} \] , \[ v(x)\ne 0 \] , \[ \forall x\in D(g) \] .

   Теорема(правило дифференцирования сложной функции). Пусть даны функции \[ \smu{1} y=f(u) \] , \[ \smu{1} u=g(x) \] , причем \[ \smu{1} E(g)\subset D(f) \] . Если существует в точке x₀ производная \[ \smu{3} g'(x_0)\equiv \frac {dg}{dx}|_{x=x_0} \] , а в точке \[ \smu{3} u_0=g(x_0) \] существует производная \[ \smu{2} f'(u_0)=\frac {df}{du}|_{u=u_0} \] , то сложная функция \[ \smu{2} {y=f(g(x))} \] имеет производную в точке x₀, определяемую из формулы (дифференцирования сложной функции):
4. \[ y'(x)=f'(u)\cdot g'(x) \] \[ (y'_x=f'_u\cdot u'_x) \] .

Найдем производные некоторых элементарных функций.

Теорема.

1. Производная постоянной равна нулю, то есть (C)'=0, C=const.
2. Производная функции y=sin x равна y'=cos x.
3. Производная функции y=cos x равна y'=-sin x.
4. Производная функции y=ln x равна \[ (\ln x)'=\frac 1x \] .
5. Имеет место формула (xⁿ)'= nx^n-1.
6. Производная показательной функции при a>0, \[ a\ne 1) \] равна: \[ (a^x)'=a^x \cdot \ln a \] ,

Следствие. Для экспоненциальной функции (e^x)'=e^x.

Докажем, например, теорему для производной натурального логарифма.

Доказательство. Для всех \[ x\in D(\ln x)=(0;+\infty) \] имеем \[ \frac {\Delta y}{\Delta x} = \frac {\ln (x+\Delta x)-\ln x}{\Delta x} = \frac {\ln \frac {x+\Delta x}{x}}{\Delta x} = \frac {\ln \Bigl(1+\frac {\Delta x}{x}\Bigr)}{\Delta x} = \ln \Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}}. \] Отсюда, \[ \lim\limits_{\Delta x\to 0} \frac {\Delta y}{\Delta x} = \lim\limits_{\Delta x\to 0}\ln \Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}} = \ln \Bigl(\lim\limits_{\Delta x\to 0}\Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}} \Bigr). \] Из замечательного предела следует, что \[ \lim\limits_{\Delta x\to 0} \Bigl(1+\frac {\Delta x}{x} \Bigr)^{\frac {1}{\Delta x}} = e^{\frac {1}{x}}. \] Следовательно, \[ \lim\limits_{\Delta x\to 0}\frac {\Delta y}{\Delta x} =\ln e^{\frac {1}{x}}=\frac 1x\ln e = \frac 1x. \] Равенство доказано.