Lecture
Векторная алгебра и аналитическая геометрия
6.1 Векторная алгебра
В геометрии вектором называется всякий направленный отрезок. Учение о действиях над векторами называется векторной алгеброй.
Вектор, началом которого служит точка А, а концом точка В, обозначается \[ \overrightarrow{AB} \] или \[ \vec{a} \] . Если начало и конец вектора совпадают, то отрезок превращается в точку и теряет направление, такой отрезок называют нуль-вектором.
Если вектор задан точками \[ A(x_1, y_1) \] и \[ B(x_2, y_2) \] , то его координаты: \[ \overrightarrow{AB}=\{(x_2-x_1), (y_2-y_1)\}=\{X,Y\} \] . Длина вектора называется также его модулем, обозначается \[ |\overrightarrow{AB}| \] или \[ |\vec{a}| \] и вычисляется по формуле:
\[ |\vec{a}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{X^2+Y^2} \]Формулы
\[ M_x=\frac{x_1+x_2}{2},M_y=\frac{y_1+y_2}{2} \]служат для вычисления координат середины отрезка \[ \overrightarrow{AB} \] .
Разделить отрезок \[ \overrightarrow{AB} \] в заданном отношении ? можно так: \[ L_{x}=\frac{x_{1}+\lambda x_{2}}{1+\lambda},L_{y}=\frac{y_{1}+\lambda y_{2}}{1+\lambda } \] , здесь \[ L_x \] и \[ L_y \] — координаты точки L, делящей отрезок в отношении \[ AL:LB=l_{1}:l_{2}=\lambda \] .
Напомним, что векторы в Octave задаются путём поэлементного ввода:
>>> a =[1 0 3] % Вектор-строка a = 1 0 3 >>> b = [0; 1; 4] % Вектор-столбец b = 0 1 4
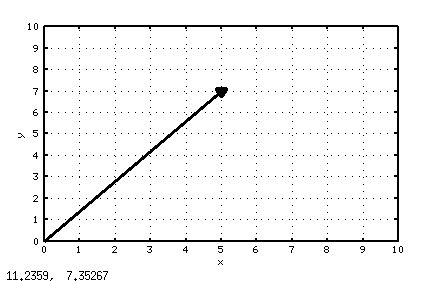
Пример 6.1. Построить вектор \[ |\vec{a}| = \{5, 7\} \] .
Решение примера показано на рис. 6.1 . Листинг 6.1 содержит команды Octave, с помощью которых был выполнен рисунок.
clear all; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0: 10]); set(gca, ’ytick’, [0: 10]); grid on; xlabel(’x’); ylabel(’y’); a =[5 7]; L1=line([0, a (1)], [0, a(2)]); set(L1, ’LineWidth’, 3, ’Color’, ’k’); L1_=line([a(1), a(1)], [a(2), a(2)]); set(L1_, ’LineWidth’, 5, ’Color’, ’k’); set(L1_, ’marker’, ’<’, ’markersize’, 16);Листинг 6.1. Построение вектора (пример 6.1).
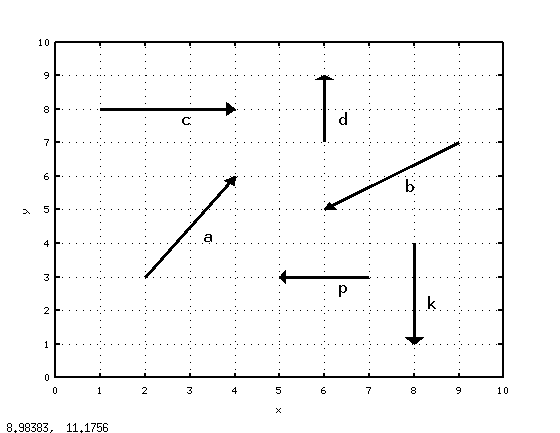
Пример 6.2. Построить векторы, заданные координатами начала и конца:
\[ \begin{array}{ccc} \vec{a}=\{(2,3),(4,6)\}, &\vec{b}=\{(9,7),(6,5)\}, &\vec{c}=\{(1,8),(4,8)\},\\ \vec{d}=\{(6,7),(6,9)\}, &\vec{k}=\{(8,4),(8,1)\}, &\vec{p}=\{(7,3),(5,3)\}. \end{array} \]Решение примера показано в листинге 6.2 и на рис. 6.2. Обратите внимание, что для изображения вектора была создана специальная функция \[ vector(A, B) \] . Эта функция изображает направленный отрезок \[ |\overrightarrow{AB}| \] в декартовой системе координат и возвращает координаты его середины. В данном случае координаты середины отрезка нужны для нанесения соответствующей надписи, обозначающей вектор на рисунке.
clear all; % Функция рисует направленный отрезок АВ, в качестве результата выдаёт % координаты середины отрезка АВ. function [M]= vector(A,B) x1=A(1); x2=B(1); y1=A(2); y2=B(2); alf =30*pi/180;% Угол в вершине стрелки в радианах L=15; % Деление отрезка в заданном отношении xm=(x1+L*x2)/(1+L); ym=(y1+L*y2)/(1+L); k1=(y2-y1)/( x2-x1); % Угол наклона прямой АВ if (k1==Inf ) | (k1==-inf) % Отрезок перпендикулярен оси Ох % Координаты основания треугольника, образующего стрелку x4=xm-0.2; y4=ym; x3=xm+0.2; y3=ym; elseif k1==0 % Отрезок перпендикулярен оси Оу x4=xm; y4=ym-0.2; x3=xm; y3=ym+0.2; else % Уравнение прямой АВ k1=(y2-y1)/(x2-x1); m1=y1-x1*(y2-y1)/(x2-x1); % Уравнение прямой перпендикулярной АВ k3=-1/k1; m3=1/k1*xm+ym; % Уравнение прямой, проходящей через точку В под углом alf к прямой АВ k2=(-k1*tan(alf))/(tan(alf)*k1-1); m2=y2-k2*x2; % Уравнение прямой, проходящей через точку В под углом -alf к прямой АВ k4=(-k1*tan(-alf))/(tan(-alf)*k1-1); m4=y2-k4*x2; % Координаты основания треугольника, образующего стрелку x4=(m3-m2)/(k2-k3); y4=k2*x4+m2; x3=(m3-m4)/(k4-k3); y3=k3*x3+m3; end; % Изображение прямой АВ line([A(1),B(1)], [A(2), B(2)], ’LineWidth’, 3, ’Color’, ’k’); % Изображение стрелки в точке В patch([x2, x3, x4], [y2, y3, y4], ’k’); % Координаты середины отрезка АВ M(1) =(x1+x2)/2; M(2) =(y1+y2)/2; end; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’); set(gcf, ’name’, ’Vector’); set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0: 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); ma=vector([2, 3], [4, 6]); % Построение вектора a T=text(ma(1)+0.3,ma(2)-0.3, ’a’); set (T, ’FontSize’, 20) mb=vector([9, 7], [6, 5]); % Построение вектора b T=text(mb(1)+0.3,mb(2)-0.3, ’b’); set(T, ’FontSize’, 20) mc=vector([1, 8], [4, 8]); % Построение вектора c T=text(mc(1) +0.3,mc(2)-0.3, ’c’); set(T, ’FontSize’, 20) md=vector([6, 7], [6, 9]); % Построение вектора d T=text(md(1)+0.3,md(2)-0.3, ’d’); set(T, ’FontSize’, 20) mk=vector([8, 4], [8, 1]); % Построение вектора k T=text(mk(1)+0.3,mk(2)-0.3, ’k’); set (T, ’FontSize’, 20) mp=vector([7, 3], [5, 3]); % Построение вектора p T=text(mp(1) +0.3,mp(2)-0.3, ’p’); set(T, ’FontSize’, 20)Листинг 6.2. Построение векторов, функция vector (пример 6.2).
Два ненулевых вектора \[ \vec{a} \] и \[ \vec{b} \] равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы равны. Во всех остальных случаях векторы не равны. Два вектора имеющие равные модули и противоположные направления, называются противоположными . Векторы лежащие на параллельных прямых называются коллинеарными.
Пример 6.3. Сравнить векторы \[ \overrightarrow{AB} \] и \[ \overrightarrow{CD} \] , \[ \overrightarrow{ON} \] , \[ \overrightarrow{OM} \] и \[ \overrightarrow{KL} \] , \[ \overrightarrow{PR} \] и \[ \overrightarrow{UV} \] заданные координатами начала и конца: \[ A(1, 2), B(3, 5), C(3, 2), D(5, 5), O(7, 9), M(6, 6), N(8, 6), K(4, 9), L(3, 6), P(9, 2), R(6, 2), U(6, 3), V(9, 3) \] .
Текст файла-сценария представлен в листинге 6.3. При решении примера была создана функция \[ dlina(X, Y) \] , которая вычисляет длину отрезка XY, заданного координатами точек \[ X(x_1, x_2) \] и \[ Y(y_1, y_2) \] . Для изображения векторов использовалась функция \[ vector(A, B) \] , описанная в примере 6.2.
Решение примера показано в конце листинга 6.3 и на рис. 6.3 . По полученным числовым результатам и геометрической интерпретации примера можно сделать вывод, что векторы \[ \overrightarrow{AB} \] и \[ \overrightarrow{CD} \] равны. Векторы \[ \overrightarrow{ON} \] и \[ \overrightarrow{OM} \] не равны, хотя у них и одинаковые длины, но направления различны. Векторы \[ \overrightarrow{ON} \] и \[ \overrightarrow{KL} \] неравны по той же причине, а векторы \[ \overrightarrow{OM} \] и \[ \overrightarrow{KL} \] равны. Векторы \[ \overrightarrow{PR} \] и \[ \overrightarrow{UV} \] — противоположные, так как имеют одинаковый модуль и противоположные направления.
function d=dlina(X,Y) % Функция возвращает длину отрезка XY d=sqrt((Y(1)-X(1))^2+(Y(2)-X(2))^2); end; clf; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) cla; set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); % Исходные данные A= [1, 2];B= [3, 5];C= [3, 2];D= [5, 5];O= [7, 9];M= [6, 6];N= [8, 6]; K= [4, 9]; L= [3, 6];P= [9, 2];R= [6, 2];U= [6, 3];V= [9, 3]; % Длины отрезков dAB=dlina(A,B) dCD=dlina(C,D) dON=dlina(O,N) dOM=dlina(O,M) dKL=dlina(K,L) dPR=dlina(P,R) dUV=dlina(U,V) % Построение вектора AB vector(A,B); A_=text(A(1)+0.3,A(2)-0.3, ’A’); set(A_, ’FontSize’, 20) B_=text(B(1)+0.3,B(2)-0.3, ’B’); set(B_, ’FontSize’, 20) % Построение вектора CD vector(C,D); C_=text(C(1)+0.3,C(2)-0.3, ’C’); set(C_, ’FontSize’, 20) D_=text(D(1)+0.3,D(2)-0.3, ’D’); set(D_, ’FontSize’, 20) % Построение вектора OM vector(O,M); O_=text(O(1)+0.3,O(2)-0.3, ’O’); set(O_, ’FontSize’, 20) M_=text(M(1)+0.3,M(2)-0.3, ’M’); set(M_, ’FontSize’, 20) % Построение вектора ON vector(O,N); O_=text(O(1)+0.3,O(2)-0.3, ’O’); set(O_, ’FontSize’, 20) N_=text(N(1)+0.3,N(2)-0.3, ’N’); set(N_, ’FontSize’, 20) % Построение вектора KL vector(K,L); K_=text(K(1)+0.3,K(2)-0.3, ’K’); set(K_, ’FontSize’, 20) L_=text(L(1)+0.3,L(2)-0.3, ’L’); set(L_, ’FontSize’, 20) % Построение вектора PR vector(P,R); P_=text(P(1)+0.3,P(2)-0.3, ’P’); set(P_, ’FontSize’, 20) R_=text(R(1)+0.3,R(2)-0.3, ’R’); set(R_, ’FontSize’, 20) % Построение вектора UV vector(U,V); U_=text(U(1)+0.3,U(2)-0.3, ’U’); set(U_, ’FontSize’, 20) V_=text(V(1)+0.3,V(2)-0.3, ’V’); set(V_, ’FontSize’, 20) % Решение примера 6.3 % Длины отрезков: AB = 3.6056 CD = 3.6056 ON = 3.1623 OM = 3.1623 KL = 3.1623 PR = 3 UV = 3Листинг 6.3. Сравнение векторов (пример 6.3).