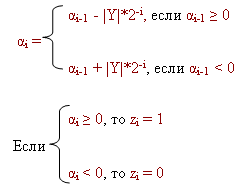Деление

Реализация операции деления в ЭВМ в двоичной системе счисления выполняется проще, чем в десятичной. Это объясняется тем, что при определении каждой цифры частного нужно сделать только одну пробу.

Если числа X и Y заданы в прямом коде, и они представлены с фиксированной запятой, то для выполнения деления используются два основных алгоритма:

• со сдвигом и автоматическим восстановлением остатка ;
• со сдвигом делителя и автоматическим восстановлением остатка.

Пусть: [X]_пк = sign X. x₁x₂..x_n

[Y]_пк = sign Y. y₁y₂..y_n

[Z]_пк = [X]_пк/[Y]_пк = sign Z. z₁z₂..z_n

X и Y должны быть такими, чтобы:

|Z| < 1 (то есть фиксированная запятая )

Деление в прямом коде со сдвигом и автоматическим восстановлением остатка

1. \[ sign\ Z = sign\ X \oplus sign\ Y \]
2. \[ |X| - |Y| = \alpha _{0} \]

3. Если \[ \alpha _{0} \ge 0 \] , то z₀ = 1 и \[ 2\alpha _{0} - |Y| = \alpha _{1} \] ( z₀ – целая часть результата).

   Если \[ \alpha _{0} < 0 \] , то z₀ = 0 и \[ 2\alpha _{0} + |Y| = \alpha _{1} \]

и т. д.

Пример:

₊0.100 = [|X|]_дк

1.010 = [-|Y|]_дк

\[ 1.110 = \alpha _{0} = [|X|]_{дк} + [-|Y|]_{дк} < 0, z_{0} = 0 \]

\[ _{+}1.100 = 2\alpha _{0} (сдвиг\ в\ ДК\ отрицательного\ числа) \]

0.110 = [|Y|]_дк

\[ 0.010 = \alpha _{1} = 2\alpha _{0} + [|Y|]_{дк} > 0,\ z_{1} = 1 \]

\[ _{+}0.100 = 2\alpha _{1} \]

1.010 = [-|Y|]_дк

\[ 1.110 = \alpha _{2} = 2\alpha _{1} + [-|Y|]_{дк} < 0, z_{2} = 0 \]

\[ _{+}1.100 = 2\alpha _{2} (сдвиг\ в\ ДК\ отрицательного\ числа) \]

0.110 = [|Y|]_дк

\[ 0.010 = \alpha _{3} = 2\alpha _{2} + [|Y|]_{дк} > 0, z_{3} = 1 \]

Ответ: [Z]_пк = 1.101

Деление в прямом коде со сдвигом делителя и автоматическим восстановлением остатка

• \[ sign\ Z = sign\ X \oplus sign\ Y \]
• \[ |X| - |Y| = \alpha _{0} \]

• Если \[ \alpha _{0} \ge 0 \] , то z₀ = 1.

  Если \[ \alpha _{0} < 0 \] , то z₀ = 0.

  

  
  

Разрядная сетка (n + d) разрядов, где d = log₂n

Пример:

1) [X]пк = 1.1001
2) [Y]пк = 1.1011
n = 4, d = 2

Ответ: [Z]_пк = 0.1100