Lecture
Построение тестов с использованием алфавитов большой значности
20.1. Построение тестов в 9,10-значном алфавите
Кроме шестизначного алфавита \[ T_{6} \] , при генерации тестов применяются алфавиты большей значности, которые позволяют более точно описывать возможные комбинации значений сигналов в исправном и неисправном устройстве и, следовательно, эффективней проводить активизацию путей в схеме [20.1]. Среди них широкое распространение получил десятизначный алфавит \[ Т_{10} \] , который кроме символов, имеющихся в алфавите \[ Т_{6} \] , включает следующие символы алфавита \[ В_{16} \] - \[ G0 \] , \[ F0 \] , \[ G1 \] , \[ F1 \] [20.2,20.3]. Таким образом, \[ T_{10}=\{\varnothing , 0, 1, D, D', G0, F0, G1, F1, u\} \] [20.2,20.3]. Иногда его дополняют еще символом \[ D^{*} \] . Каждый из добавленных в \[ T_{10} \] символов соответствует двум возможным комбинациям базового алфавита \[ B_{4} \] . Символ \[ G0 \] показывает, что в исправной схеме значение сигнала на данной линии равно 0, а в неисправной - 0 или 1. Аналогично \[ G1 \] означает - 1 в исправной схеме, а в неисправной - 0 или 1. Символ \[ F0 \] показывает, что в неисправном ДУ значение сигнала равно 0, а в исправном - 0 или 1. Аналогично \[ F1 \] соответствует - 1 в неисправном ДУ и 0 или 1 в исправном. Введение дополнительных символов позволяет в некоторых случаях уменьшить неопределенность в процессе построения теста по сравнению с алфавитом \[ Т_{6} \] . Повышение мощности алфавита может уменьшить перебор вариантов при поиске решения. Например, возможны ситуации, когда построение теста в алфавите \[ Т_{6} \] идет с перебором, а в алфавитах \[ Т_{10} \] (и большей значности) тест строится без перебора. Если существует \[ k \] путей от места неисправности до внешнего выхода, то \[ D \] -алгоритм в худшем случае, например для избыточной неисправности пытается активизировать \[ 2^{k} - 1 \] многомерных путей. С другой стороны, алфавит \[ Т_{10} \] позволяет строить тесты с помощью только одномерной активизации в худшем случае \[ k \] путей.
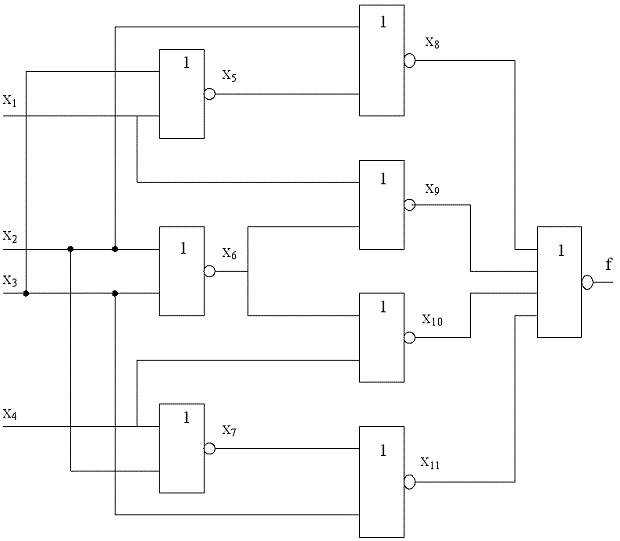
Рассмотрим схему, изображенную на рис. 20.1. Если значение линии \[ x_{3} \] равно \[ D \] , то значение линии \[ x_{6} \] будет равно либо \[ D \] , либо 0, в зависимости от того, какое значение будет на линии \[ x_{4} \] - 0 или 1. Очевидно, что это соответствует установлению на линии \[ x_{6} \] значения \[ F0 \] . Аналогично, при \[ x_{6}=F0 \] значение линии \[ x_{11} \] будет равно либо \[ D' \] , либо 1 в зависимости от того, какое значение будет на линии \[ x_{9} \] . То есть линии \[ x_{11} \] нужно присвоить значение \[ F1 \] . Заметим, что здесь на линиях \[ x_{6} \] и \[ x_{11} \] неопределенность уменьшилась с четырех возможных комбинаций до двух (это невозможно сделать в алфавите \[ Т_{6} \] ). На линии \[ x_{10} \] в зависимости от значения \[ x_{1} \] будет 0, 1 или \[ D' \] . Поскольку в алфавите \[ Т_{10} \] нет символа для этой ситуации, то линии \[ x_{10} \] присваивается неопределенное значение \[ u \] . При этом происходит огрубление вследствие недостаточной мощности алфавита \[ Т_{10} \] (в алфавите \[ B_{16} \] результат был бы точнее). Символ \[ D^{*} \] может возникнуть, например, на выходе вентиля "исключающее ИЛИ", если один из его входов примет значение \[ D(D') \] .
| \[ И \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
|---|---|---|---|---|---|---|---|---|---|---|
| \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] | \[ 0 \] |
| \[ 1 \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
| \[ D \] | \[ 0 \] | \[ D \] | \[ D \] | \[ 0 \] | \[ D \] | \[ F0 \] | \[ 0 \] | \[ F0 \] | \[ F0 \] | \[ F0 \] |
| \[ D' \] | \[ 0 \] | \[ D' \] | \[ 0 \] | \[ D' \] | \[ G0 \] | \[ D' \] | \[ G0 \] | \[ 0 \] | \[ G0 \] | \[ G0 \] |
| \[ G1 \] | \[ 0 \] | \[ G1 \] | \[ D \] | \[ G0 \] | \[ G1 \] | \[ U \] | \[ G0 \] | \[ F0 \] | \[ U \] | \[ u \] |
| \[ F1 \] | \[ 0 \] | \[ F1 \] | \[ F0 \] | \[ D' \] | \[ U \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ U \] | \[ u \] |
| \[ G0 \] | \[ 0 \] | \[ G0 \] | \[ 0 \] | \[ G0 \] | \[ G0 \] | \[ G0 \] | \[ G0 \] | \[ 0 \] | \[ G0 \] | \[ G0 \] |
| \[ F0 \] | \[ 0 \] | \[ F0 \] | \[ F0 \] | \[ 0 \] | \[ F0 \] | \[ F0 \] | \[ 0 \] | \[ F0 \] | \[ F0 \] | \[ F0 \] |
| \[ D^{*} \] | \[ 0 \] | \[ D^{*} \] | \[ F0 \] | \[ G0 \] | \[ U \] | \[ U \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
| \[ U \] | \[ 0 \] | \[ U \] | \[ F0 \] | \[ G0 \] | \[ U \] | \[ U \] | \[ G0 \] | \[ F0 \] | \[ U \] | \[ u \] |
| \[ ИЛИ \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
|---|---|---|---|---|---|---|---|---|---|---|
| \[ 0 \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
| \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] | \[ 1 \] |
| \[ D \] | \[ D \] | \[ 1 \] | \[ D \] | \[ 1 \] | \[ G1 \] | \[ 1 \] | \[ G1 \] | \[ D \] | \[ G1 \] | \[ G1 \] |
| \[ D' \] | \[ D' \] | \[ 1 \] | \[ 1 \] | \[ D' \] | \[ F1 \] | \[ F1 \] | \[ D' \] | \[ F1 \] | \[ F1 \] | \[ F1 \] |
| \[ G1 \] | \[ G1 \] | \[ 1 \] | \[ G1 \] | \[ F1 \] | \[ G1 \] | \[ U \] | \[ U \] | \[ G1 \] | \[ G1 \] | \[ G1 \] |
| \[ F1 \] | \[ F1 \] | \[ 1 \] | \[ 1 \] | \[ F1 \] | \[ U \] | \[ F1 \] | \[ F1 \] | \[ U \] | \[ F1 \] | \[ F1 \] |
| \[ G0 \] | \[ G0 \] | \[ 1 \] | \[ G1 \] | \[ D' \] | \[ U \] | \[ F1 \] | \[ G0 \] | \[ U \] | \[ D^{*} \] | \[ u \] |
| \[ F0 \] | \[ F0 \] | \[ 1 \] | \[ D \] | \[ F1 \] | \[ G1 \] | \[ U \] | \[ U \] | \[ F0 \] | \[ U \] | \[ u \] |
| \[ D^{*} \] | \[ D^{*} \] | \[ 1 \] | \[ G1 \] | \[ F1 \] | \[ G1 \] | \[ F1 \] | \[ D^{*} \] | \[ U \] | \[ D^{*} \] | \[ u \] |
| \[ U \] | \[ U \] | \[ 1 \] | \[ G1 \] | \[ F1 \] | \[ G1 \] | \[ F1 \] | \[ U \] | \[ U \] | \[ U \] | \[ u \] |
| НЕ | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G1 \] | \[ F1 \] | \[ D^{*} \] | \[ u \] |
|---|---|---|---|---|---|---|---|---|---|---|
| \[ 1 \] | \[ 0 \] | \[ D' \] | \[ D \] | \[ G0 \] | \[ F0 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
| \[ \oplus \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
|---|---|---|---|---|---|---|---|---|---|---|
| \[ 0 \] | \[ 0 \] | \[ 1 \] | \[ D \] | \[ D' \] | \[ G1 \] | \[ F1 \] | \[ G0 \] | \[ F0 \] | \[ D^{*} \] | \[ u \] |
| \[ 1 \] | \[ 1 \] | \[ 0 \] | \[ D' \] | \[ D \] | \[ G0 \] | \[ F0 \] | \[ G1 \] | \[ F1 \] | \[ D^{*} \] | \[ u \] |
| \[ D \] | \[ D \] | \[ D' \] | \[ 0 \] | \[ 1 \] | \[ G0 \] | \[ F1 \] | \[ G1 \] | \[ F0 \] | \[ U \] | \[ D^{*} \] |
| \[ D' \] | \[ D' \] | \[ D \] | \[ 1 \] | \[ 0 \] | \[ G1 \] | \[ F0 \] | \[ G0 \] | \[ F1 \] | \[ U \] | \[ D^{*} \] |
| \[ G1 \] | \[ G1 \] | \[ G0 \] | \[ G0 \] | \[ G1 \] | \[ G0 \] | \[ U \] | \[ G0 \] | \[ U \] | \[ U \] | \[ u \] |
| \[ F1 \] | \[ F1 \] | \[ F0 \] | \[ F \] | \[ F0 \] | \[ U \] | \[ F0 \] | \[ U \] | \[ F1 \] | \[ U \] | \[ u \] |
| \[ G0 \] | \[ G0 \] | \[ G1 \] | \[ G1 \] | \[ G0 \] | \[ G1 \] | \[ U \] | \[ G0 \] | \[ U \] | \[ U \] | \[ U \] |
| \[ F0 \] | \[ F0 \] | \[ F1 \] | \[ F0 \] | \[ F1 \] | \[ U \] | \[ F1 \] | \[ U \] | \[ F0 \] | \[ U \] | \[ U \] |
| \[ D^{*} \] | \[ D^{*} \] | \[ D^{*} \] | \[ u \] | \[ U \] | \[ U \] | \[ U \] | \[ U \] | \[ U \] | \[ U \] | \[ D^{*} \] |
| \[ U \] | \[ U \] | \[ U \] | \[ D^{*} \] | \[ D^{*} \] | \[ U \] | \[ U \] | \[ U \] | \[ u \] | \[ D^{*} \] | \[ U \] |
Распространение значений \[ F0 \] , \[ F1 \] , \[ G0 \] , \[ G1 \] , \[ D^{*} \] назовем обобщенным D-распространением, а процедуру, с помощью которой это выполняется - обобщенным D-проходом. Эта процедура выполняется для вентилей с помощью многозначных таблиц, которые представлены в табл. 20.1-табл. 20.4. Отметим, что эти таблицы могут быть получены с помощью универсальной модели, описанной в "Система многозначных алфавитов и функций" , функций \[ f^0, f^{D'}, f^D, f^1 \] [20.3] (если получается код символа, не принадлежащего алфавиту \[ T_{10} \] , то он заменяется символом неопределенности \[ u \] ). Линии, имеющие значения \[ D \] , \[ D' \] , \[ G0 \] , \[ G1 \] , \[ F0 \] , \[ F1 \] образуют обобщенную D-границу.
Рассмотрим построение теста для неисправности \[ x_{6}\equiv 0 \] в схеме рис. 20.1. Линии \[ x_{6} \] присваиваем значение \[ D \] . Продвижение назад дает \[ x_{2}=x_{3}=0 \] . Выполнив обобщенное \[ D \] -распространение, получим \[ x_{9}=x_{10}=G0 \] . Для \[ D \] -распространения выбираем \[ x_{9}= D' \] (путем выбора из \[ 0 \] и \[ D' \] снимаем неопределенность до символа \[ D' \] ). Импликация приводит к установке \[ x_{5}=1 \] , \[ x_{8}=0 \] . Далее в результате обобщенного \[ D \] -распространения получаем \[ f=F0 \] . Для \[ D \] -распространения полагаем \[ f=D \] (опять снимаем неопределенность путем выбора нужной комбинации \[ D \] из двух возможных). Продвижение назад, определяет \[ x_{4}=0 \] . Таким образом, тестом является набор \[ x_{1}=x_{2}=x_{3}=x_{4}=0 \] .