Lecture
Повышение эффективности корпоративных производственно-сбытовых структур (ПСС) в области сбыта и товаропродвижения
Цель построения иерархии - получение приоритетных элементов на последнем уровне (альтернатив) при наилучшем отображении воздействия (в данном случае балльного показателя) на вершине иерархии.
- Принцип сравнительных суждений.
С помощью данного принципа можно установить приоритеты критериев и оценить каждую альтернативу по этим критериям. В методе анализа иерархий для более точного определения весов критериев целесообразно использовать способ парных сравнений. Группа экспертов (ее выбор зависит от специфики задачи) заполняет анкеты с указанием превосходства одного критерия над другим (число от 1/9 до 9), оценивая их по шкале относительной важности (табл. 6.5).
Таблица 6.5. Шкала относительной важности Относительная важность Определение Пояснения 1 равная важность критериев равный вклад двух критериев в достижение цели 3 легкое или умеренное превосходство одного над другим опыт или суждения дают легкое превосходство одного критерия над другим 5 существенное или сильное превосходство опыт или суждения дают сильное превосходство 7 значительное превосходство одному виду критерия дается значительное превосходство 9 очень сильное превосходство очевидное превосходство одного критерия над другим 2, 4, 6, 8 промежуточное между двумя соседними суждениями применяется в компромиссном случае 1/2, 1/3, \[ \dots \] показатель, обратный вышеуказанным целым величинам В итоге получается квадратная симметричная матрица - матрица попарных сравнений ("матрица суждений", табл. 6.6), отражающая влияние критериев на поставленную цель.
Таблица 6.6. Матрица попарных сравнений (матрица суждений) Критерии \[ A_{1} \] \[ A_{2} \] \[ A_{3} \] \[ \dots A_n \] \[ A_{1} \] \[ w_{1}/w_{1} \] \[ w_{1}/w_{2} \] \[ w_{1}/ w_{3} \] \[ \dots \] \[ A_{2} \] \[ w_{2}/w_{1} \] \[ w_{2}/w_{2} \] \[ w_{2}/w_{3} \] \[ \dots \] \[ A_{3} \] \[ w_{3}/w_{1} \] \[ w_{3}/w_{2} \] \[ w_{3}/w_{3} \] \[ \dots \] \[ \dots \\ A_{n} \] \[ \dots \\ w_{n}/w_{1} \] \[ \dots \\ w_{n}/w_{2} \] \[ \dots \\ w_{n}/w_{3} \] \[ \dots \\ w_{n}/w_{n} \] Имеющиеся альтернативы аналогично сравниваются по каждому из критериев с помощью статистических или других данных (рис. 6.23):
- Синтез приоритетов.
На данном этапе получаются осмысленные подходы к многокритериальной проблеме планирования с помощью сочетания иерархической декомпозиции и шкалы относительной важности.
Из группы матриц парных сравнений формируется набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.
Существует много способов расчета и аппроксимации критериев. В данном примере одним из наилучших путей является геометрическое среднее. Необходимо вычислить множество собственных векторов для каждой матрицы, а затем нормализовать результаты к единице, получая тем самым вектор приоритетов (собственный вектор).
Удельный вес в общем случае вычисляется по формуле:
Для случая \[ n = 4 \] (где \[ n \] - число сравниваемых элементов или критериев) расчетные формулы имеют следующий вид:
Оценка компонентов собственного вектора по строкам:
\[ \begin{array}{c} \sqrt[4]{ \cfrac{W_1\cdot W_1\cdot W_1\cdot W_1}{W_1\cdot W_2\cdot W_3\cdot W_4}} \equiv a \\ \sqrt[4]{ \cfrac{W_2\cdot W_2\cdot W_2\cdot W_2}{W_1\cdot W_2\cdot W_3\cdot W_4}} \equiv b \\ \sqrt[4]{ \cfrac{W_3\cdot W_3\cdot W_3\cdot W_3}{W_1\cdot W_2\cdot W_3\cdot W_4}} \equiv c \\ \sqrt[4]{ \cfrac{W_4\cdot W_4\cdot W_4\cdot W_4}{W_1\cdot W_2\cdot W_3\cdot W_4}} \equiv d \end{array} \]Затем необходимо сложить элементы столбцов и нормализовать их:
\[ \begin{array}{c} X_1 = \cfrac{a}{a+b+c+d} \\ \dots\dots\dots\dots\dots\dots \\ X_4 = \cfrac{d}{a+b+c+d} \end{array} \]Таким образом, получается вектор приоритетов \[ X = (X_{1},\dots , X_{4}) \] . Величины значимости по каждому элементу \[ У = (Y _{1},\dots ,Y_{4}) \] получаются путем умножения матрицы сравнений на вектор приоритетов (или удельные веса элементов) \[ X = (X_{1},\dots , X_{4}) \] :
\[ \left | \begin{array}{cccc} w_1/w_1 & w_1/w_2 & w_1/w_3 & w_1/w_1 \\ w_2/w_1 & w_2/w_2 & w_2/w_3 & w_2/w_2 \\ w_3/w_1 & w_3/w_2 & w_3/w_3 & w_3/w_3 \\ w_4/w_1 & w_4/w_2 & w_4/w_3 & w_4/w_4 \\ \end{array} \right | \times \left | \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right | \]То есть:
\[ \begin{array}{c} Y_1 = \cfrac{W_1}{W_1}X_1 + \cfrac{W_1}{W_2}X_2 + \cfrac{W_1}{W_3}X_3 + \cfrac{W_1}{W_4}X_4 \\ \dots\dots\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \\ Y_4 = \cfrac{W_4}{W_1}X_1 + \cfrac{W_4}{W_2}X_2 + \cfrac{W_4}{W_3}X_3 + \cfrac{W_4}{W_4}X_4 \\ \end{array} \]Для определения приоритета альтернатив необходимо на основе рассчитываемых выше по "матрицам согласования" векторов аналогично вычислить удельный вес каждого варианта относительно главной цели \[ X_{i} \] .
| Критерий \[ А_1 \] | 1 | 2 | \[ \dots \] | 9 | Критерий \[ А_2 \] | 1 | 2 | \[ \dots \] | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | \[ W_i / W_j \] | 2 | 1 | \[ W_i / W_j \] | ||||
| \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | ||||
| 9 | 1 | 9 | 1 | ||||||
| Критерий \[ А_3 \] | 1 | 2 | \[ \dots \] | 9 | Критерий \[ А_4 \] | 1 | 2 | \[ \dots \] | 9 |
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | \[ W_i / W_j \] | 2 | 1 | \[ W_i / W_j \] | ||||
| \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | ||||
| 9 | 1 | 9 | 1 | ||||||
| Критерий \[ А_5 \] | 1 | 2 | \[ \dots \] | 9 | Критерий \[ А_{\dots} \] | 1 | 2 | \[ \dots \] | 9 |
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | \[ W_i / W_j \] | 2 | 1 | \[ W_i / W_j \] | ||||
| \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | ||||
| 9 | 1 | 9 | 1 | ||||||
| Критерий \[ А_{\dots} \] | 1 | 2 | \[ \dots \] | 9 | Критерий \[ А_9 \] | 1 | 2 | \[ \dots \] | 9 |
| 1 | 1 | 1 | 1 | ||||||
| 2 | 1 | \[ W_i / W_j \] | 2 | 1 | \[ W_i / W_j \] | ||||
| \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | \[ \dots \] | \[ W_j / W_i \] | \[ \dots \] | ||||
| 9 | 1 | 9 | 1 |
Для оценки достоверности (корректности) проставленных исходных данных рассчитывается индекс согласованности (ИС). Сначала вычисляется величина:
\[ \lambda_{max} = \sum\limits_{i=1}^{n}{\cfrac{W_i}{W_1}X_1} + \sum\limits_{i=1}^{n}{\cfrac{W_i}{W_2}X_2} + \sum\limits_{i=1}^{n}{\cfrac{W_i}{W_3}X_3} + \cdots + \sum\limits_{i=1}^{n}{\cfrac{W_i}{W_n}X_n} \]После ее расчета можно получить ИС, отражающий степень нарушения численной и порядковой согласованности:
\[ ИС = (\lambda_{max}-n)?(n-1) \]Теперь необходимо сравнить эту величину с той, которая получилась бы при случайном выборе количественных суждений из шкалы \[ 1/9, 1/8, \dots , 1, 2, \dots 9 \] . Ниже даны средние согласованности для случайных матриц разного порядка, полученные Т. Саати и К. Кернсом и изложенные в их книге [22] - табл. 6.7.
| Порядок матрицы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| СС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Тогда относительная согласованность ( \[ ОС \] ), по которой судят о правильности суждения, равна:
\[ ОС= ИС / CС \]Если индекс \[ ОС < 10 \% \] ,то полученный результат по определению приоритетов достоверен. В отдельных случаях допускается величина до 20%. Если же \[ ОС \] выходит из этих пределов, то участникам необходимо более подробно исследовать задачу, проверить свои суждения, уточнить статистические данные или провести новые эксперименты.
Если индекс \[ ОС \] находится в нужных пределах, то составляется сводная таблица, в которую входят вектор приоритетов (нормализованных весов) критериев и все векторы приоритетов (превосходства) альтернатив.
На основе полученных данных получается нормализованный показатель \[ X_{i}, \] отражающий рейтинг альтернатив по решаемой проблеме.
В данном случае среди предложенных альтернативных вариантов распределения продукции выбирается тот вариант, который имеет максимальный удельный вес. Сортировка полученных значений удельных весов в порядке убывания устанавливает очередность других вариантов сбытовых структур в случае невозможности внедрения по тем или иным причинам базового варианта.
Таким образом, для различных видов товара и типов рынка руководство ПСС может моделировать деятельность системы распределения пятью вышеперечисленными методами. Это позволяет создавать оптимальную организационную структуру системы сбыта ПСС, состоящую из определенного количества элементов сети на каждом уровне. В дальнейшем по данным моделям можно оптимизировать логистические процессы, охватывающие товародвижение готовой продукции по всем уровням ПСС.
6.3. Система выбора организационной структуры сбыта ПСС и мероприятий по их совершенствованию
Разработка системы управления сбытовыми системами для достижения поставленных целей по объемам сбыта. Для практической реализации методов моделирования структур сбыта и систем товародвижения руководству ПСС рекомендуется создать организационную структуру (отдел) для проведения необходимых исследований и расчетов. В данную группу рекомендуется набирать специалистов из маркетингового отдела, отдела логистики, финансового отдела и бухгалтерии. Также к работе могут быть привлечены специалисты со стороны и само руководство ПСС.
В качестве задачи перед отобранной группой специалистов имеет смысл поставить выявление общих направлений повышения эффективности деятельности ПСС [9, 29]. В первую очередь это повышение объемов реализации, пути достижения которых изображены в виде схемы на рис. 6.23. Отобранная руководством группа специалистов должна проработать все направления по достижению поставленных задач по сбыту.
На вершине схемы указана основная цель: повышение объемов реализации продукции исходя из максимального удовлетворения потребителей при оптимальном использовании материальных и временных ресурсов. В формальном виде цель - это эффективность ПСС из формулы (6.1) \[ П \to max \] .
В общем случае достичь целевых объемов сбыта при ограниченных ресурсах можно за счет трех основных составляющих:
- снижения себестоимости (для производственных организаций) или стоимости приобретения продукции (для торговых предприятий) \[ S_{prod.} \] ;
- оптимизации (снижения) коммерческих расходов и расходов на продажу \[ S_{post.}, S_{per.} \] ;
- стимулирования сбыта и других маркетинговых составляющих; (поскольку данная работа не посвящена маркетинговым приемам повышения спроса, такие мероприятия, как реклама, стимулирование потребителей, и подобные действия в алгоритме не рассматриваются).
Снижения себестоимости можно добиться за счет сокращения прямых производственных затрат по любым статьям калькуляции [5], начиная от стоимости сырья и заканчивая расходами на содержание и эксплуатацию оборудования. В данной лекции производственная составляющая стоимости изделия не рассматривается.
Для торговых организаций необходимо снижать стоимость приобретения товара без потери качества. Этого можно добиться только путем переговоров с поставщиками или снижения таможенных пошлин и сборов (если организация занимается импортом).
Оптимизация коммерческих расходов и расходов на содержание всей ПСС полностью зависит от организации системы управления снабженческосбытовой сети ПСС. Значительную долю в расходах, особенно в торговых предприятиях, составляют транспортные и складские расходы. Именно в данном направлении следует наиболее полно использовать методы оптимизации транспортной логистики, входящей в логистику снабжения и в логистику сбыта. Необходимо совершенствовать структуру ПСС, систему внутрифирменного управления и каналы товародвижения.
Как видно из данной схемы (рис. 6.23), одной из важных составляющих успешной деятельности организации является формирование оптимальной снабженческосбытовой сети ПСС. В первую очередь это создание оптимальной сбытовой структуры и системы товародвижения. Теоретические основы построения и методы моделирования сбытовых структур были изложены в предыдущем разделе. Необходимо разработать систему управления сбытовыми процессами, по которой будет работать группа исследователей для выработки рекомендаций.
В общем случае модель управления процессом организации снабженческосбытовой структуры ПСС состоит из ряда блоков.
Блок А1 "Маркетинговые исследования" посвящен изучению рынка товара, анализу внешних и внутренних факторов ПСС. Выходом данного блока является информация о рынке сбыта, в частности о типе рынка, конкуренции, рыночной конъюнктуре. Производится оценка спроса, рассчитанная по методике, изложенной выше.
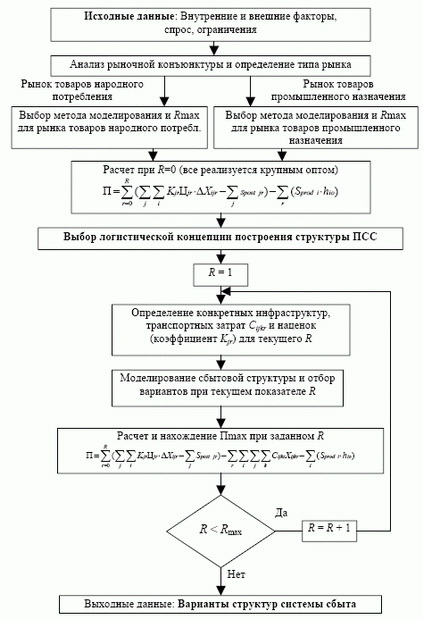
Блок А2 посвящен моделированию и выбору принципиальных структур сбыта, а блок А3 - выбору конкретной структуры и разработке системы товародвижения ПСС как в статическом, так и динамическом плане. В Блоке А2 заключен алгоритм предварительного отбора вариантов структур и товародвижения в ПСС при различных уровнях системы сбыта на основе критерия максимума \[ NPV \] - рис. 6.24.
Первоначально для отдельно взятой ПСС происходит анализ внутренних и внешних факторов. Группа специалистов исследует рынок по изделиям номенклатуры \[ m \] . В финансовом отделе запрашивается покупная стоимость изделий \[ S_{prod.} \] , в маркетинговом отделе определяется потенциальный спрос при различной сбытовой политике \[ H_{i} \] .