2.5.5. Одноканальная СМО с конечной надежностью

Построить граф состояний одноканальной СМО с очередью на три заявки и с конечной надежностью каналов обслуживания. При отказе канала обслуживания заявка, находившаяся на обслуживании, теряется. Процессы в системе - марковские.

Описание состояний СМО:

\[ S_{0} ... S_{4} \] - состояния исправной СМО;

\[ S^{'}_{0} ... S^{'}_{4} \] - состояния неисправной СМО.

Обозначения:

\[ \lambda \] - интенсивность поступления заявок;

\[ \mu \] - интенсивность обработки заявки каналом;

\[ \nu \] - интенсивность поломок канала;

\[ \eta \] - интенсивность ремонта неисправного канала.

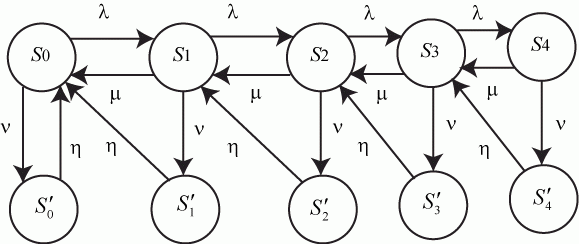
Граф состояний СМО с конечной надежностью каналов обслуживания приведен на рис. 2.14.

Если в состоянии \[ S_{0} \] (канал свободен, в очереди заявок нет) система выйти из строя не может, то состояния \[ S^{'}_{0} \] нет. Так как при отказе заявка, находившаяся на обслуживании, теряется, то после восстановления переход осуществляется к предыдущему состоянию, например, из состояния \[ S^{'}_{3} \] в состояние \[ S_{2} \] .

Эта модель не является моделью "гибели и размножения". Поэтому соответствующие вероятности находятся решением системы линейных алгебраических уравнений, полученных из уравнений Колмогорова для стационарного режима.

2.6. Метод динамики средних. Сущность и содержание метода

В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.

Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгованных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний \[ p_{i} \] , так как

\[ \overline{n} = \sum\limits_{i = 0}^n {{p_{i}*n_{i}}}. \]

Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.

Например, в соединении имеется 100 радиостанций. Каждая из них может находиться в боевых условиях в пяти состояниях:

\[ S_{1} \] - исправна, работает, не обнаружена;

\[ S_{2} \] - исправна, работает, обнаружена;

\[ S_{3} \] - работоспособна, но подавлена помехами;

\[ S_{4} \] - обнаружена, поражена;

\[ S_{5} \] - находится в ремонте.

Для определения средних численностей каждого из этих состояний пришлось бы составить \[ 5^{100} \] уравнений Колмогорова. Очевидно, такое моделирование не годится.

В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних.

Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.

Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет элементов и состояний, тем точнее результат математического моделирования.

Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками:

• в системе протекает случайный марковский процесс;
• элементы системы однородны в том смысле, что состояния, их число и их вероятности - одинаковые;
• элементы меняют состояния независимо друг от друга.

Цель моделирования: определить средние количества элементов (математические ожидания) \[ m_{i}(t) \] , находящихся в одинаковых состояниях \[ S_{i} \] , и дисперсию \[ D_{i}(t) \] .

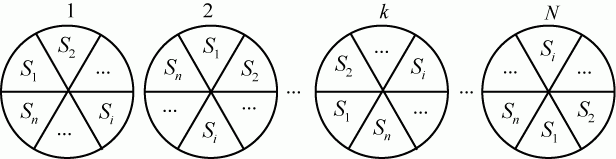
Схематично такая система может быть представлена так, как показано на рис. 2.15.

Система имеет \[ N \] элементов, а каждый элемент имеет \[ n \] состояний. Численность \[ i \] -го состояния на любой момент времени - величина случайная. Обозначим ее \[ x_{i}(t) \] . Матожидание и дисперсия этой случайной величины:

\[ m_{i}(t) = M[x_{i}(t)],\;D_{i}(t) = D[x_{i}(t)]. \]

В дальнейшем для лучшей обозримости формул аргумент \[ t \] писать не будем:

\[ m_{i} = M[x_{i}],\;D_{i} = D[x_{i}]. \]

Введем переменную \[ x^k \] так что:

\[ x_{i}^k = \left \{ \begin {array}{ll} 1, & \text{если } k\text{-й элемент находится в состоянии } i,\;\text{вероятность } p_{i};\\ 0, & \text{если } k\text{-й элемент не находится в состоянии } i,\;\text{вероятность } (1 - p_{i}). \end{array} \]

Отсюда следует, что случайная величина \[ x_{i} \] равна:

\[ x_{i} = \sum\limits_{k = 1}^{N}{x_{i}^k}. \]

В силу однородности элементов и независимости состояний случайная величина \[ x_{i} \] имеет биномиальное распределение (распределение Бернулли) с матожиданием и дисперсией соответственно:

\[ M[x_{i}] = Np_{i},\;D[x_{i}] = Np_{i}(1 - p_{i}) \]

или окончательно

\[ m_{i} = Np_{i},\;D_{i} = Np_{i}(1 - p_{i}) = m_{i}\left ( 1 - \cfrac{m_{i}}{N} \right ). \]

Равенство \[ m_{i} = Np_{i} \] связывает вероятность \[ i \] -го состояния элемента в произвольный момент времени с матожиданием численности этих состояний по всем элементам.

Определять значения \[ p_{i} \] для одного элемента мы умеем. Для этого достаточно составить систему уравнений Колмогорова и решить ее.

Вспомним, что система уравнений Колмогорова для одного элемента содержит \[ n \] уравнений, для всех \[ N \] элементов - \[ n^N \] , а метод динамики средних в \[ n^{N - 1} \] раз меньше. В этом и состоит выигрыш, который дает применение метода динамики средних.

Порядок моделирования с использованием метода динамики средних заключается в следующем.

1. Описать состояния одного элемента системы.
2. Составить размеченный граф состояний для одного элемента, указав рядом с каждым состоянием \[ S_{1},S_{2}, \ldots ,S_{i}, \ldots ,S_{n} \] средние численности состояний \[ m_{1},m_{2}, \ldots ,m_{i}, \ldots ,m_{n} \] , полученные умножением \[ Np_{i} \] .
3. Составить дифференциальные уравнения (ДУ) по следующим правилам:
   • производная средней численности состояния равна сумме стольких членов, сколько стрелок связано с данным состоянием;
   • если стрелка направлена из состояния, член имеет знак минус, если в состояние - знак плюс;
   • каждый член равен произведению интенсивности потока событий, переводящего элемент по данной стрелке, на среднюю численность того состояния, из которого исходит стрелка.
4. Решить систему дифференциальных уравнений относительно \[ m_{i} \] .
5. Вычислить значения дисперсий \[ D_{i} \] и средних квадратических отклонений \[ \sigma_{i} = \sqrt{D_{i}} \] .

Поскольку процессы в элементах - марковские, то справедливы все рассуждения об установившихся значениях \[ m_{i} \] , об условиях существования установившихся значений \[ m_{i}(t) = m_{i} \] .

Полученные уравнения для \[ m_{i} \] называют уже не уравнениями Колмогорова, а уравнениями динамики средних. Поскольку они получаются из уравнений Колмогорова путем умножения всех членов на постоянное число \[ N \] , то их можно писать сразу для средних численностей состояний \[ m_{i} \] по образцу уравнений для вероятностей \[ p_{i} \] .

Рассмотрим на примере методику моделирования с использованием метода динамики средних.

Пример 2.8. В части имеются 100 средств связи (СС). СС выходят из строя с интенсивностью \[ \lambda_{12} \] . При нахождении СС в неисправном состоянии проводится его диагностика, в результате чего оно может быть отправлено в ремонтное подразделение части (интенсивность отправки \[ \lambda_{23} \] ), либо во внешнее ремонтное подразделение (интенсивность отправки \[ \lambda_{24} \] ), либо списано (интенсивность списания \[ \lambda_{c} \] ). В ремонтном подразделении части СС ремонтируются с интенсивностью \[ \lambda_{31} \] , а во внешнем ремонтном подразделении - с интенсивностью \[ \lambda_{41} \] . СС части пополняются с интенсивностью \[ \lambda_{п} \] , в среднем равной интенсивности списания.

Требуется провести моделирование с целью определения средних численностей каждого состояния СС.

Решение

1. Описание состояний одного средства связи

   Система может иметь следующие четыре состояния:

   \[ S_{1} \] - СС исправно;

   \[ S_{2} \] - СС неисправно, производится диагностика;

   \[ S_{3} \] - СС находится на ремонте в ремонтном подразделении части;

   \[ S_{4} \] - СС находится на ремонте во внешнем ремонтном подразделении.
2. Построение размеченного графа состояний

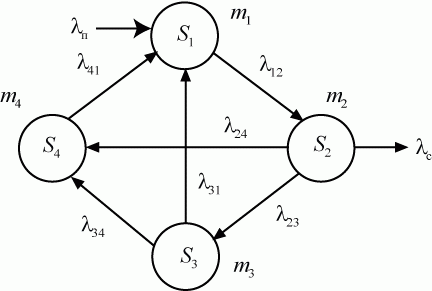
   Размеченный граф состояний представлен на рис. 2.16.

   

   
   Рис. 2.16. Размеченный граф состояний системы ремонта
3. Составление системы дифференциальных уравнений

   Каждое уравнение системы составляется по тому же правилу, что и система дифференциальных уравнений Колмогорова.

   \[ \left \{ \begin{array}{l} \cfrac{dm_1}{dt} = -\lambda_{12}m_1 + \lambda_{31}m_3 + \lambda_{41}m_4 + \lambda_{11}m_2\\ \cfrac{dm_2}{dt} = -\lambda_{23}m_2 - \lambda_{24}m_2 - \lambda_{c}m_2 + \lambda_{12}m_1\\ \cfrac{dm_3}{dt} = -\lambda_{31}m_3 + \lambda_{23}m_2\\ \cfrac{dm_4}{dt} = -\lambda_{41}m_4 + \lambda_{24}m_2\\ \end{array} \]

   Численности состояний являются функциями времени, т. е. \[ m_{i} = m_{i}(t) \] . В системе дифференциальных уравнений запись упрощена. Выражение для пополняющего члена написано из условия равенства в среднем пополнения и убыли \[ \lambda_{c}m_{п} = \lambda_{2}m_{2} \] . Также мы не можем воспользоваться нормировочным условием \[ \sum\limits_{i = 1}^4{m_{i}(t)} = 100 \] , так как в силу случайного характера списания и пополнения в некоторые моменты времени оно может не выполняться. Общее число СС в части при этом меняется со временем:

   \[ N\left( t \right) = N + \int\limits_0^t {{\lambda _{п}}\left( t \right)dt} - \int\limits_0^t {{\lambda _{с}}\left( t \right)dt} \]
4. Решение системы дифференциальных уравнений относительно m_{i}

   Решить систему ДУ можно методом численного интегрирования, например, Рунге-Кутта, задав начальные значения численностей состояний для момента \[ t = 0 \] :

   \[ m_{1}(0) = 100,\;m_{2}(0) = 0,\;m_{3}(0) = 0,\;m_{4}(0) = 0, \]

   считая интенсивности \[ \lambda_{ij},\;\lambda_{c},\;\lambda_{п} \] известными.
5. Вычисление дисперсий и среднеквадратических отклонений

   Дисперсия вычисляется по формуле:

   \[ D_{i} = m_{i}\left [1 - \left ( m_{i} / \sum\limits_{i = 1}^4{m_{i}} \right ) \right ],\;i = \overline{1,4} \]

   По дисперсии определяется среднеквадратическое отклонение численности состояний \[ \sigma_{i} = \sqrt{D_{i}} \] и находится диапазон возможных значений численности \[ S_{i} \] состояния \[ m_{i} \pm 3\sigma_{i} \] .

Метод динамики средних справедлив и для предельных значений численностей состояний. В данной задаче уравнения динамики средних - система линейных алгебраических уравнений:

\[ \left \{ \begin{array}{l} 0 = - \lambda_{12}m_{1} + \lambda_{31}m_{3} + \lambda_{41}m_{4} + \lambda_{11}m_{2};\\ 0 = - \lambda_{23}m_{2} - \lambda_{24}m_{2} - \lambda_{c}m_{2} + \lambda_{12}m_{1};\\ 0 = - \lambda_{31}m_{3} + \lambda_{23}m_{2};\\ 0 = - \lambda_{41}m_{4} + \lambda_{24}m_{2}. \end{array} \]

Однако прежде чем переходить к этим уравнениям, нужно сначала убедиться, что стационарные значения \[ m_{i} \] существуют. Здесь численности состояний \[ m_{i} \] не являются функциями времени. Поэтому можно воспользоваться нормировочным условием.