Сравнения и матрицы

3.2. Линейное уравнение

Криптография часто включает в себя решение уравнения или множества уравнений одной или более переменных с коэффициентом в Z_n. Этот раздел показывает, как решать уравнения с одним неизвестным, когда степень переменной равна 1 (линейное уравнение).

Линейные уравнения с одним неизвестным, содержащие сравнения

Давайте посмотрим, как решаются уравнения с одним неизвестным, содержащие сравнения, то есть уравнения ax = b (mod n). Уравнение этого типа может не иметь ни одного решения или иметь ограниченное число решений. Предположим, что НОД (a, n) = d. Если d†b, решение не существует. Если d|b, то имеется d решений.

Если d|b, то для того, чтобы найти решения, мы используем следующую стратегию.

1. Сократить уравнение, разделив обе стороны уравнения (включая модуль) на d.
2. Умножить обе стороны сокращенного уравнения на мультипликативную инверсию, чтобы найти конкретное решение x₀.
3. Общие решения будут x = x₀ + k (n/d) для k = 0, 1..., (d – 1).

Пример 3.8

Решить уравнение \[ 10x \equiv 2(\bmod 15) \] .

Сначала мы найдем НОД(10,15) = 5. Полученное число 5 не делится на 2, решение отсутствует.

Пример 3.9

Решить уравнение \[ 14x \equiv 12(\bmod 18) \] .

Решение

Заметим, что НОД (14, 18) = 2. Поскольку 2 делит 12, мы имеем точно два решения, но сначала сократим уравнение:

Оба решения, 6 и 15, удовлетворяют уравнению сравнения, потому что \[ (14 \times 6)\bmod 18 = 12 \] , а также \[ (14 \times 15)\bmod 18 = 12 \] .

Пример 3.10

Решить уравнение \[ 3x + 4 \equiv 6\left( {\bmod 13} \right) \] .

Решение

Сначала мы приводим уравнение к форме \[ ax \equiv b(\bmod n) \] . Мы прибавляем (–4) к обеим сторонам ( 4 аддитивная инверсия). Получим \[ 3x \equiv 2(\bmod 13) \] . Поскольку НОД (3, 13) = 1, уравнение имеет только одно решение, \[ {x_0} = (2 \times {3^{ - 1}})\bmod 13 = 18 \mod 13 = 5 \] . Мы можем видеть, что ответ удовлетворяет первоначальному уравнению: \[ 3 \times 5 + 4 = 6\left( {\bmod 13} \right) \] .

Система линейных уравнений, содержащих сравнения

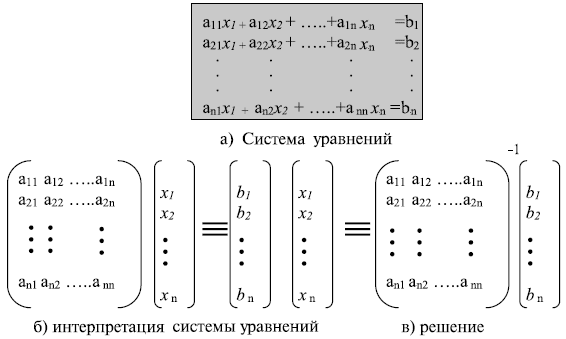
Мы можем решить систему линейных уравнений с одним и тем же модулем, если матрица, сформированная из коэффициентов системы уравнений, имеет обратную матрицу. Для решения уравнения составляются три матрицы. Первая — квадратная матрица — формируется из коэффициентов уравнения. Вторая — матрица-столбец — составляется из переменных. Третья — матрица-столбец в правой стороне оператора сравнения — состоит из значения b_n. Мы можем это уравнение представить как произведение матриц. Если обе стороны сравнения умножить на мультипликативную инверсию первой матрицы, в результате мы получим решение системы уравнений, как это показано на рис. 3.9.

Рис. 3.9. Система линейных уравнений

Пример 3.11

Решить систему следующих трех уравнений:

3x + 5y + 7z = 3 (mod 16) 
x + 4y + 13z = 5 (mod 16)
2x + 7y + 3z = 4 (mod 16)

Решение

Здесь x, y и z играют роли x₁, x₂, и x₃. Матрица, сформированная из коэффициентов уравнений, — обратима. Мы находим мультипликативную инверсию матрицы и умножаем ее на матрицу столбца, сформированную из 3, 5 и 4. Результат — \[ x \equiv 15(\bmod 16) \] , \[ y \equiv 4(\bmod 16) \] и \[ z \equiv 14(\bmod 16) \] . Мы можем проверить ответ, подставляя эти значения в уравнения.