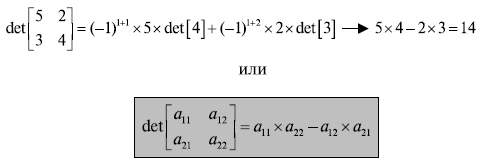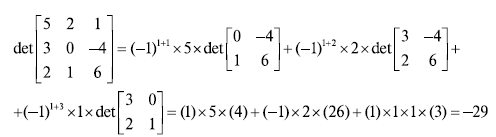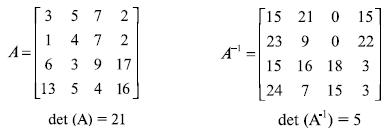Детерминант

Детерминант — квадратная матрица A размера \[ m \times m \] , обозначаемая как det (A) — скалярное вычисление рекурсивно, как это показано ниже:

Пример 3.5

Рисунок 3.6 показывает, как можно вычислить детерминант матрицы \[ 2 \times 2 \] , базируясь на детерминанте матрицы \[ 1 \times 1 \] и используя приведенное выше рекурсивное определение. Пример доказывает, что когда m 1 или 2, это позволяет найти детерминант матрицы достаточно просто.

Рис. 3.6. Вычисление детерминанта матрицы 2 x 2

Пример 3.6

Рисунок 3.7 показывает вычисление детерминанта матрицы \[ 3 \times 3 \] .

Рис. 3.7. Вычисление детераминаната матрицы 3 x 3

Инверсии

Матрицы имеют аддитивные и мультипликативные инверсии.

Аддитивная инверсия

Аддитивная инверсия матрицы — это другая матрица B, такая, что A + B = 0. Другими словами, мы имеем элементы b_ij = –a_ij для всех значений i и j. Обычно аддитивная инверсия A обозначается как (-A).

Мультипликативная инверсия

Мультипликативная инверсия определена только для квадратных матриц. Мультипликативная инверсия квадратной матрицы A — квадратная матрица B, такая, что \[ A \times B = B \times A = I \] . Обычно мультипликативная инверсия обозначается как A^-1. Мультипликативная инверсия существует только, если det (A) имеет мультипликативную инверсию в соответствующем инверсном множестве. Если целое число не имеет мультипликативной инверсии в Z, то не существует мультипликативной инверсии матрицы в Z. Однако матрицы с реальными элементами имеют инверсии, только если \[ \det \left( A \right) \ne 0 \] .

Матрицы вычетов

Криптография использует матрицы вычетов: матрицы могут содержать все элементы из Z_n. Все операции на матрицах вычетов выполняются так же, как и на матрицах целых чисел, за исключением того, что операции производятся в модульной арифметике. Есть одно интересное свойство: матрица вычетов имеет мультипликативную инверсию, если детерминант матрицы имеет мультипликативную инверсию в Z_n. Другими словами, матрица вычета имеет мультипликативную инверсию, если НОД (det (A), n) = 1.

Пример 3.7

Рисунок 3.8 показывает матрицу вычетов в Z_n и его мультипликативной инверсии A^-1. Возьмем детерминант det (A) = 21, который имеет мультипликативную инверсию 5 в Z₂₆. Обратите внимание, что когда мы умножаем эти две матрицы, то результат — единичная матрица мультипликативная матрица, в Z₂₆.

Рис. 3.8. Матрица вычетов и мультипликативная инверсия

Сравнение

Две матрицы, сравнимые по модулю n, записываются как \[ A \equiv B(\bmod n) \] , если они имеют одинаковое число строк и столбцов и все соответствующие элементы — сравнимые по модулю n. Другими словами, \[ A \equiv B(\bmod n) \] , если \[ {a_{ij}} \equiv {b_{ij}}(\bmod n) \] для всех i и j.