К настоящему моменту у нас должно быть сформировано первое понимание того, как устроены структуры данных во время выполнения программы: это совокупность объектов, связанных ссылками. Пришло время посмотреть на управляющие структуры, определяющие порядок, в котором будут применяться операторы к этим объектам.

7.1. Структуры для решения задач

Возможно, вы знакомы с известной пародией на то, как учат инженеров.

Как вскипятить чайник воды

1. Если вода холодная: поставьте чайник на огонь, дождитесь, пока она закипит.
2. Если вода горячая: дождитесь, пока она остынет. Условие случая 1 выполнено. Примените случай 1.

Как способ кипячения воды эта техника не особенно эффективна, но дан прекрасный пример комбинирования некоторых из фундаментальных управляющих структур.

• Выбор: "Если данное условие выполняется, то делай одно, иначе — делай другое".
• Последовательность: "Делай вначале одно, потом другое".
• Подпрограмма позволяет нам именовать способ решения некоторой проблемы (возможно параметризованный) и повторно использовать его в подходящем контексте.

Полезно вспомнить обсуждение контрактов в предыдущих лекциях. Здесь мы отмечаем, что переход к случаю 1 из случая 2 возможен — что явно подчеркнуто при описании случая 2, — поскольку первый шаг случая 2 гарантирует выполнение предусловия случая 1 (вода холодная). Предусловия и другие контракты будут играть большую роль в получении правильных структур управления.

В этом примере в непринужденной манере устанавливается подходящий контекст изучения управляющих структур: они задают приемы решения задачи. Программа дает решение задачи; каждый вид управляющей структуры отражает частичную стратегию поиска решения задачи.

Задача всегда будет ставиться так: начиная с известного свойства K, требуется достичь некоторой цели G. В примере: свойство K — чайник с водой, цель G — вскипятить воду. Стратегии, обеспечиваемые управляющими структурами, состоят в редуцировании (приведении) задачи к нескольким более простым задачам. Вот пример.

• Можно применять управляющую структуру-последовательность, если удается сформулировать частную цель I, такую что обе новые проблемы проще исходной (достижение цели G непосредственно из K): достичь I из K, достичь G из I. Зная, как решить первую и вторую проблему, управляющая структура-последовательность решит вначале первую проблему, а затем вторую.
• Управляющая структура выбора представляет стратегию разбиения множества начальных возможных ситуаций K на две или более непересекающиеся области, так что становится проще решать задачу независимо на каждой из областей.
• Структура-цикл, которую мы еще увидим в примерах, является стратегией повторяющегося решения задачи на подмножествах (возможно, тривиальных). Подмножества расширяются до тех пор, пока не покроют всю область.
• Управляющая структура-подпрограмма (процедура или функция) является стратегией решения задачи, основанной на обнаружении того, что наша задача сводится к решению другой (часто более общей задачи), решение которой уже известно.

Техника рекурсии, достаточно важная, чтобы посвятить ей отдельную лекцию, может быть применена, если можно сконструировать решение задачи из одного или нескольких решений той же самой задачи, но примененной к данным меньшего размера.

Так как программирование предназначено для решения задач, полезно изучать эти и другие структуры с этих позиций.

Для каждой из управляющих структур будем последовательно анализировать:

• общую идею, приводя примеры;
• синтаксис конструкции в соответствующем языке;
• семантику: эффект исполнения — как управляющая структура задает порядок выполнения входящих в нее операторов;
• корректность: правила, основанные на принципах Проектирования по Контракту. Это позволит нам убедиться, что семантика соответствует намерениям и что управляющая структура при выполнении дает имеющий смысл результат, не приводя к поломке выполнения программы или к другим неприятным следствиям.

7.2. Понятие алгоритма

Управляющие структуры определяют порядок операций в процессах, выполняемых компьютером. Такие процессы называются алгоритмами. Это одна из фундаментальных концепций информатики. Вам уже наверняка приходилось встречаться с этим термином, поскольку даже популярная пресса обсуждает такие темы, как "криптографические алгоритмы". Для изучения управляющих структур нам понадобится более точное определение.

Пример

В общих терминах алгоритм — это описание процесса вычислений, достаточное, чтобы его могла выполнить машина (для нас в роли машины выступает компьютер), осуществление процесса на любых входных данных без дальнейших инструкций. Нам известно много различных алгоритмов. Сложите два числа:

687 + 42 = 729

Для решения этой задачи вы примените правила, скорее всего, не думая явно об этих правилах.

Почувствуй Арифметику

Сложение двух целых чисел

Процесс состоит из нескольких шагов, каждый шаг выполняется над определенной позицией чисел. Позиция для первого шага задается самой правой цифрой обоих чисел. Для каждого следующего шага его позиция - непосредственно слева от предыдущей позиции. У каждого шага есть перенос. Начальный перенос равен нулю. На каждом шаге пусть m - это цифра первого числа, стоящая в позиции данного шага, а n - это соответствующая цифра второго числа в той же позиции. Если какое-либо число не имеет цифр в данной позиции, то значение (m или n) равно нулю.

На каждом шаге процесс выполняет следующее:

1. вычисляет s - сумму трех значений: m, n и переноса;
2. если s меньше 10, запишет s в позицию шага для результата и установит значение переноса равным нулю;
3. если s равно 10 или больше, запишет s - 10 в позицию шага для результата и установит значение переноса равным 1. Записанное значение s - 10 является цифрой, так как s не может быть больше 19.

Процесс заканчивается, когда в позиции шага нет цифр у обоих чисел и перенос равен нулю.

Этап 3 основан на предположении: "s не может быть больше 19". Без него процесс не имел бы смысла, так как мы хотим писать в результат цифру за цифрой. Чтобы гарантировать корректность алгоритма, нам нужно доказать, что это свойство выполняется на каждом шаге процесса. Действительно, m и n являются цифрами, не могут быть больше 9, а их сумма не больше 18. Так как перенос не больше 1, s не больше 19. Это пример инвариантного свойства, концепции, которую будем изучать детально при рассмотрении циклов.

Явно и точно: алгоритмы против рецептов

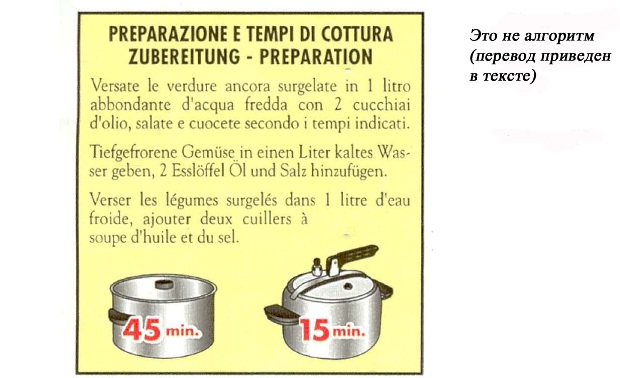
Будучи менее точной, чем принятый стандарт публикации алгоритмов, предыдущая спецификация все же более пунктуальна, чем большинство предписаний, которые нам приходится использовать с различной степенью успеха в обычной жизни. Вот пример инструкции на трех языках на пакете куриного супа с овощами.

На немецком и французском языках инструкция говорит: "Залейте овощи одним литром холодной воды, добавьте две столовые ложки масла и соль". Рецепт не точен, поскольку "столовые ложки" бывают разными, и сколько нужно соли, тоже не указано. Что более удивительно, так это отсутствие ключевой инструкции: если вы хотите получить результат, то без огня не обойтись. Только итальянская версия упоминает эту деталь — "Готовьте в соответствии с указанным временем", что придает смысл рисунку.

Рис. 7.1. Это не алгоритм (перевод приведен в тексте)

Такие инструкции ориентированы на человека, его интерпретацию; отсутствие явно заданных шагов не представляет проблемы, поскольку большинству пользователей ясно, что еду не приготовишь без кипячения и что картинка задает время приготовления супа (даже я догадался). Но то, что годится для кухонных рецептов, недостаточно для алгоритмов. Вы должны специфицировать каждую операцию, каждую деталь процесса, и их нужно специфицировать в форме, не оставляющей двусмысленностей, никакой свободы для предположений.

Свойства алгоритма

Для алгоритмов в противоположность неформальным рецептам справедливы свойства, задаваемые следующим определением.

Определение: Алгоритм

Алгоритм является спецификацией процесса, действующей на (возможно пустом) множестве данных и удовлетворяющей следующим пяти правилам.

А1. Спецификация определяет применимое множество данных.

А2. Спецификация определяет множество элементарных действий, из которых строятся все шаги процесса.

А3. Спецификация определяет возможный порядок или порядки, в которых процесс может выполнять свои действия.

А4. Спецификация элементарных действий (правило А2) и предписанный порядок (правило А3) основаны на точно определенных соглашениях, позволяя процессу выполняться автоматически, без вмешательства человека. Гарантируется, что на одном и том же множестве данных результат будет одинаковым для двух автоматов, следующих тем же соглашениям.

А5. Для любого множества данных, для которых процесс применим (по правилу А1), гарантируется завершение процесса после выполнения конечного числа шагов алгоритма.

Вышеприведенный метод сложения целых обладает требуемыми свойствами:

А1: описывает процесс, применимый к некоторым данным, и специфицирует вид этих данных: два целых числа, записанные в десятичной нотации;

А2: процесс основан на хорошо определенных базисных действиях: установить значение, равное нулю или известному числу, сложить три числа (цифры), сравнить число с 10;

A3: описание задает порядок выполнения базисных действий;

А4: правило является точным. Этой точности должно быть достаточно для любых двух людей, понимающих и применяющих алгоритм одинаковым способом. Хотя, как отмечалось, оно может быть недостаточно точным для других целей;

А5: для любых применимых данных — два числа в десятичной нотации — процесс завершится после конечного числа шагов. Это интуитивно ясно, но должно быть тщательно проверено. Мы увидим, как это делается, показав, что выражение M — step + 1 является вариантом.

В определении правила A3 упоминается "порядок или порядки" шагов. Последовательный и детерминированный алгоритм определяет единственный порядок шагов для любого возможного выполнения. Но это не единственная возможность.

• Недетерминированные алгоритмы для некоторых шагов определяют множество действий, одно из которых должно быть выполнено, но алгоритм не определяет, какое именно. Вероятностный алгоритм определяет как специальный случай случайную стратегию для такого выбора.
• Параллельные алгоритмы задают для некоторых шагов множество действий, выполняемых параллельно, что применимо для вычислительных сетей и многоядерных компьютеров.

В этой книге будут рассматриваться только последовательные детерминированные алгоритмы.

Алгоритмы против програм

В свете приведенного определения алгоритма хотелось бы понять, что же отличает алгоритмы от программ? Базисные концепции одни и те же.

Иногда говорят, что разница лежит в уровне абстракции: программа предполагает выполнение на специальной машине, в то время как алгоритм задает абстрактное определение процесса вычислений независимо от любого вычислительного устройства. Это имело некоторый смысл несколько десятилетий назад, когда программы записывались в кодах конкретного компьютера. Алгоритмы тогда служили для выражения сущности программ: вычислительный процесс описывался независимо от любого компьютера. Но та точка зрения не применима сегодня.

• Для представления программ мы можем использовать ясную, высокоуровневую нотацию, определенную на уровне абстракции, который существенно превосходит детали любого компьютера. Нотация языка Eiffel, используемая в этой книге, является примером.
• Для представления алгоритма способом, полностью отвечающим требованиям определения, в частности, требованию точности — условие А4 — также необходима нотация с точно определенным синтаксисом и семантикой, что в конечном итоге делает эту нотацию эквивалентной языку программирования.

Практическое описание алгоритмов часто опускает специфицирование некоторых деталей, таких как выбор структур данных, которые программа не может опустить, так как без этого невозможна компиляция и выполнение. Эта практика, кажется, обосновывает довод о более высоком уровне абстракции алгоритмов в сравнении с программами. Но для алгоритмов это только полезное соглашение, облегчающее их публикацию. В описаниях, предназначенных для публикации, снижаются требования к точности (условие А4), но каждый читатель понимает, что для получения алгоритма в настоящем смысле необходимо восстановить опущенные детали.

Так что мы не можем полагать, что уровень абстракции отличает алгоритмы от программ. Более важны другие два отличия — или нюанса.

• Алгоритм описывает единственный вычислительный процесс. Десятилетия назад в этом же состояла цель каждой типичной программы: "Начислить зарплату!". Сегодня программа включает множество алгоритмов. Мы уже видели образец в системе Traffic (отобразить линию, анимировать линию, отобразить маршрут ...), и таких примеров множество. Подобное наблюдение применимо к любому серьезному программному продукту. Вот почему в этой книге чаще используется термин "система", а не "программа" (которую часто по-прежнему воспринимают как решение одной задачи).
• Как важно в программе описать шаги процесса обработки, так же важно и описать в ней структуры данных — в ОО-подходе структуру объектов, — к которым эти шаги применяются. Этот критерий не является абсолютным, так как реально нельзя отделить алгоритмические шаги от структур данных, которыми они манипулируют. Но при описании программистских концепций иногда хочется большее внимание уделить аспекту обработки — алгоритму в узком смысле этого термина, — а иногда аспекту данных. Это объясняет заглавие классической книги по программированию Никласа Вирта (опубликованной в 1976):

  Algorithms + Data Structures = Programs.
  На русском языке: "Алгоритмы + Структуры данных = Программы"
  

Рис. 7.2. Вирт (2005)

ОО-подход к конструированию ПО отводит центральную роль данным, более точно — типам объектов: классам. Каждый алгоритм присоединен к некоторому классу. Eiffel применяет это правило без исключений: каждый алгоритм, который вы пишете, появляется как метод (feature) некоторого класса. Этот подход оправдан по соображениям качества создаваемого ПО, которое будем анализировать в последующих лекциях. Как следствие, в этой книге мы будем изучать алгоритмы и аспекты данных в тесном взаимодействии.

Структуры управления, рассматриваемые в этой лекции, являются одним из примеров алгоритмических концепций, не связанных напрямую с конкретным видом структуры данных.