Общие сведения, установка

Введение

Курс посвящен GNU Octave — одной из самых интересных прикладных программ для решения инженерных и математических задач.

GNU Octave — это свободный интерпретирующий язык для проведения математических вычислений. По возможностям и качеству реализации интерпретатора язык Octave можно сравнивать с проприетарной программой MATLAB, причём синтаксис обоих языков очень схож.

Существуют версии языка для различных дистрибутивов GNU Linux (ALT Linux, Debian, Ubuntu, Mandriva и др.) и для ОС Windows. На наш взгляд, GNU Octave больше ориентирован на работу в Linux. Работа в ОС Windows возможна, но пользователю Windows надо быть готовым работать с простым текстовым редактором и командной строкой.

Когда авторы начинали знакомиться с GNU Octave, основной проблемой было отсутствие хорошего русскоязычного введения в этот язык. Наша книга является попыткой восполнить этот пробел. Поэтому большое внимание было уделено самому языку (глава 3), операциям с матрицами (глава 5) и графическим возможностям пакета (глава 4).

Наш многолетний опыт преподавания информационных дисциплин в Донецком национальном техническом университете говорит нам о том, что студенту и инженеру наряду с описанием функций, предназначенных для решения той или иной задачи, не лишним будет напомнить и математическую постановку решаемой задачи, а зачастую и численные методы решения задачи. Именно поэтому в ряде глав приведены не только описания функций, но и описаны численные методы решения задач.

Что касается графических оболочек, таких как qtOctave, Xoctave и Kalculus, нами принято решение кратко описать наиболее стабильную из них, qtOctave, а основное внимание в книге уделить собственно языку. Мы считаем, что GNU Octave — это в первую очередь мощный интерпретирующий язык. Зная его, пользователь сможет работать с любой графической оболочкой.

Авторы выражают благодарность компании ALT Linux за многолетнее сотрудничество и возможность издать очередную книгу.

Авторы заинтересованы в общении с читателями. Мы ждём ваши замечания и отзывы по адресам EAlekseev@gmail.com и chesn_o@list.ru.

Донецк, апрель 2012

1.1 Принципы работы с интерпретатором

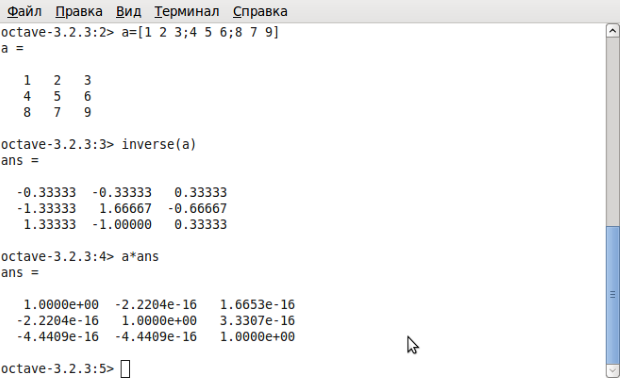
Octave — высокоуровневый интерпретируемый язык программирования, предназначенный для решения задач вычислительной математики. В состав пакета входит интерактивный командный интерфейс (интерпретатор Octave). Интерпретатор Octave запускается из терминала ОС Linux или из его порта в Windows. После запуска Octave пользователь видит окно интерпретатора (рис. 1.1).

В окне интерпретатора пользователь может вводить как отдельные команды языка Octave, так и группы команд, объединяемые в программы. Если строка заканчивается символом ";", результаты на экран не выводятся. Если же в конце строки символ ";" отсутствует,

Рис. 1.1. Окно интерпретатора Octave

Рис. 1.2. Использование символов ";" и "%" в Octave

результаты работы выводятся на экран (рис. 1.2). Текст в строке после символа \[ \% \] (процент) является комментарием и интерпретатором не обрабатывается (рис. 1.2). (Строки комментариев авторы книги будут использовать для пояснения функций и текстов программ.) Рассмотрим несколько несложных примеров.

Пример 1.1. Решить систему линейных алгебраических уравнений (СЛАУ)

Возможны два варианта решения любой задачи в Octave:

1. Терминальный режим. В этом режиме в окно интерпретатора последовательно вводятся отдельные команды.
2. Программный режим. В этом режиме создаётся текстовый файл с расширением .m, в котором хранятся последовательно выполняемые команды Octave. Затем этот текстовый файл (программа на языке Octave) запускается на выполнение в среде Octave.

Для решения СЛАУ в окне интерпретатора Octave последовательно введём следующие команды:

% Определение матрицы коэффициентов системы линейных уравнений.
A=[3 5 -7; 3 -4 33; 22 -11 17];
b=[11; 25; 22]; % Вектор правых частей СЛАУ.
x=A^(-1)*b % Решение системы методом обратной матрицы.
x=
	1.56361
	2.55742
	0.92542
octave -3.2.3:27 > A*x % Проверка.
ans =
	11.000
	25.000
	22.000

Рис. 1.3. Программа для решения примера 1.1

В переменной \[ ans \] хранится результат последней операции, если команда не содержит знака присваивания. Следует помнить, что значение переменной \[ ans \] изменяется после каждого вызова команды без операции присваивания.

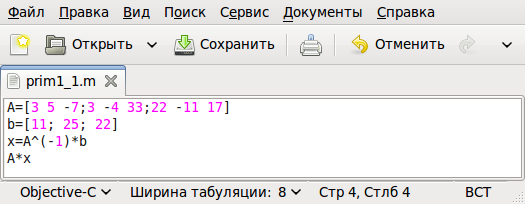
Теперь рассмотрим, как решить эту же задачу в программном режиме. Вызовем любой текстовый редактор. (Именно текстовый редактор! Не путайте с текстовыми процессорами типа Microsoft Word или OpenOffice.org/LibreOffice Writer.) Например gedit, в окне которого последовательно введём следующие команды:

A=[3 5 -7; 3 -4 33; 22 -11 17]
b =[11; 25; 22]
x=A^(-1)*b
A*x

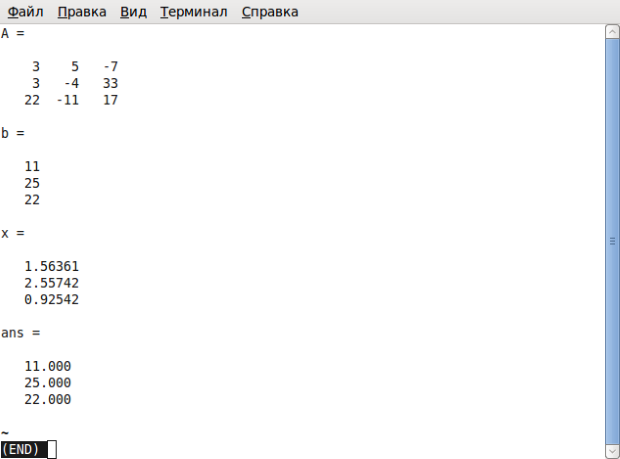
Сохраним введённые команды в виде файла с расширением .m, например, /home/evgeniy/prim1_1.m (рис. 1.3). Теперь эту программу необходимо запустить на выполнение из интерпретатора. Для этого в окне интерпретатора введём команды:

cd ’/home/evgeniy’% Переход в каталог, где хранится программа.
prim1_1 % Запуск программы.

Рис. 1.4. Окно терминала после запуска программы prim1_1

Окно интерпретатора примет вид, представленный на рис. 1.4. Просмотрев результаты работы программы, нажмите \[ q \] для возвращения в режим ввода команд терминала.