|
Это в лекции 3. |
Эквивалентность формул и нормальные формы
Дизъюнктивные и конъюнктивные нормальные формы
Определение ДНФ и КНФ
В этом разделе мы интересуемся представлением произвольной булевой
функции посредством формул специального вида, использующих только
операции 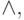
 и
и 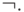
Пусть 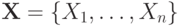 - это множество
пропозициональных
переменных. Введем для каждого i=1,...,n обозначения:
- это множество
пропозициональных
переменных. Введем для каждого i=1,...,n обозначения: 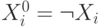 и
и 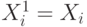 .
Формула
.
Формула  ,
в которой
,
в которой 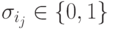 и все переменные разные, т.е.
и все переменные разные, т.е. 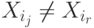 при
при 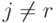 ,
называется элементарной конъюнкцией ( элементарной дизъюнкцией ).
,
называется элементарной конъюнкцией ( элементарной дизъюнкцией ).
Определение 4.2. Формула 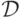 называется дизъюнктивной нормальной формой (ДНФ),
если она является дизъюнкцией элементарных конъюнкций, т.е. имеет вид
называется дизъюнктивной нормальной формой (ДНФ),
если она является дизъюнкцией элементарных конъюнкций, т.е. имеет вид  ,
где каждая формула
,
где каждая формула  - это элементарная конъюнкция .
- это элементарная конъюнкция . 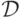 называется совершенной ДНФ, если в каждую из
ее конъюнкций
называется совершенной ДНФ, если в каждую из
ее конъюнкций  входят все
входят все  переменных из
переменных из  .
Аналогично, формула
.
Аналогично, формула  называется конъюнктивной нормальной формой (КНФ),
если она является конъюнкцией элементарных дизъюнкций,
т.е.
называется конъюнктивной нормальной формой (КНФ),
если она является конъюнкцией элементарных дизъюнкций,
т.е.  ,
где каждая формула Dj (j=1,...,r)
- это элементарная дизъюнкция . Она является совершенной КНФ,
если в каждую Dj
входят все n переменных из
,
где каждая формула Dj (j=1,...,r)
- это элементарная дизъюнкция . Она является совершенной КНФ,
если в каждую Dj
входят все n переменных из  .
.
Совершенные ДНФ и КНФ
Рассмотрим произвольную булеву функцию f(X1,...,Xn)
, зависящую
от переменных из  . Oбозначим через Nf+
множество наборов значений переменных, на которых f принимает значение 1, а через Nf-
множество наборов, на которых f принимает значение 0,
т.е.
. Oбозначим через Nf+
множество наборов значений переменных, на которых f принимает значение 1, а через Nf-
множество наборов, на которых f принимает значение 0,
т.е.  и
и  .
.
Определим по этим множествам две формулы:
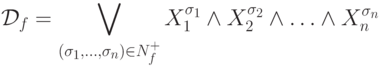
и
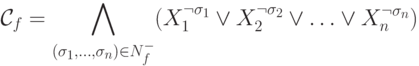
Теорема 4.1.
- Если функция f не равна тождественно 0, то
формула
 - это совершенная ДНФ, задающая функцию f.
- это совершенная ДНФ, задающая функцию f. - Если функция f не равна тождественно 1, то
формула
 - это совершенная КНФ, задающая функцию f.
- это совершенная КНФ, задающая функцию f.
Доказательство получается непосредственным вычислением значения каждой из указанных
формул с учетом того, что для любого 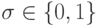 имеют место равенства:
имеют место равенства: 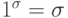 и
и 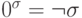 (см. задачу 4.4).
(см. задачу 4.4).
Следствие 4.1.1. Каждая булева функция может быть задана формулой, содержащей переменные и функции конъюнкции, дизъюнкции и отрицания.
Приведенные выше формулы для  и
и  позволяют
эффективно строить совершенные ДНФ и КН по табличному представлению
функции f (Каким образом?). Можно ли получить такие специальные
представления по произвольной формуле, задающей f, не выписывая ее
полной таблицы? Приводимая ниже процедура позволяет это сделать, используя основные эквивалентности формул.
позволяют
эффективно строить совершенные ДНФ и КН по табличному представлению
функции f (Каким образом?). Можно ли получить такие специальные
представления по произвольной формуле, задающей f, не выписывая ее
полной таблицы? Приводимая ниже процедура позволяет это сделать, используя основные эквивалентности формул.
Процедура Приведение к совершенной ДНФ
Вход: формула  включающая функции
включающая функции  и +.
и +.
- Используя эквивалентность (7), заменить все вхождения
функции
 в
в  на
на 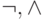 и
и 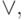 затем использовать эквивалентность (8) для замены всех вхождений функции +
на
затем использовать эквивалентность (8) для замены всех вхождений функции +
на 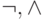 и
и 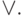
- Используя законы де Моргана (5) и снятия двойного отрицания (4), внести все знаки отрицания внутрь скобок так, чтобы все оставшиеся отрицания находились непосредственно перед переменными.
- Получившаяся после шага (2) формула
 имеет одну из
двух форм:
имеет одну из
двух форм:-
 или
или -
 .
.
Поскольку каждая из формул
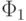 ,
,  имеет
меньшую глубину, чем формула
имеет
меньшую глубину, чем формула 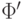 , то предположим по индукции, что для них
уже построены эквивалентные ДНФ
, то предположим по индукции, что для них
уже построены эквивалентные ДНФ 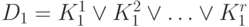 и
и 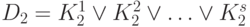 , соответственно.
, соответственно.Тогда в случае (а) имеем:
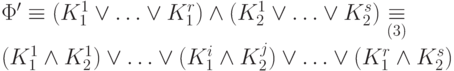
Каждый член
 этой дизъюнкции представляет собой
конъюнкцию переменных и их отрицаний. Применяя эквивалентности групп (1), (2) и
(6), можно удалить из нее повторения переменных, после чего она превратится
в некоторую элементарную конъюнкцию или константу. Проделав такие
преобразования со всеми парами (i,j), 1 <= i <= r, 1 <= j <= s, и удалив, если
потребуется, константы 0,
мы получим ДНФ, эквивалентную исходной формуле
этой дизъюнкции представляет собой
конъюнкцию переменных и их отрицаний. Применяя эквивалентности групп (1), (2) и
(6), можно удалить из нее повторения переменных, после чего она превратится
в некоторую элементарную конъюнкцию или константу. Проделав такие
преобразования со всеми парами (i,j), 1 <= i <= r, 1 <= j <= s, и удалив, если
потребуется, константы 0,
мы получим ДНФ, эквивалентную исходной формуле 
-
- Используя эквивалентности групп (1), (2) и (6), удалить из получившейся после шага (3) формулы повторные вхождения одинаковых конъюнкций.
- Пусть после шага (4) получилась ДНФ
 .
Чтобы получить эквивалентную совершенную ДНФ, построим для
каждой Ki (i=1,..., m)
, эквивалентную совершенную ДНФ
(см. задачу 4.5),заменим ею Ki
, а затем устраним повторения одинаковых
конъюнкций.
.
Чтобы получить эквивалентную совершенную ДНФ, построим для
каждой Ki (i=1,..., m)
, эквивалентную совершенную ДНФ
(см. задачу 4.5),заменим ею Ki
, а затем устраним повторения одинаковых
конъюнкций.
Из формулировок эквивалентностей (7) и (8) непосредственно вытекает
Предложение 4.1.
На этапе (1) процедуры при последовательном выполнении преобразований
(7), а затем - (8), до тех пор, пока ни одно из них не применимо, полученная
в результате формула не будет содержать функций  и +.
и +.
Доказательство этого предложения оставляем в виде упражнения (см. задачу 4.7).
Следующее утверждение гарантирует корректность этапа (2).
Предложение 4.2. На этапе (2) процедуры при любом порядке выполнения преобразований групп (4) и (5) до тех пор, пока ни одно из них не применимо, в полученной в результате формуле все знаки отрицания будут стоять непосредственно перед переменными.
Перед доказательством этого утверждения введем некоторые обозначения.
Напомним, что в определениях 3.2 и 3.3 для каждой формулы  была определена
ее глубина
была определена
ее глубина  .
Например, формула
.
Например, формула 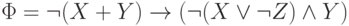 ,
построенная над системой
,
построенная над системой 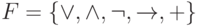 ,
имеет глубину
,
имеет глубину 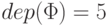 .
.
Пусть  - это формула над
- это формула над  .
Определим для каждой ее "отрицательной" подформулы вида
.
Определим для каждой ее "отрицательной" подформулы вида  высоту
высоту  как
как  . И пусть высота всей формулы
. И пусть высота всей формулы  равна сумме высот
всех ее отрицательных подформул. Например, для приведенной выше формулы
равна сумме высот
всех ее отрицательных подформул. Например, для приведенной выше формулы  ее высота
равна
ее высота
равна  .
.
Доказательство предложения 4.2 проведем индукцией по высоте формул.
Базис индукции. Если 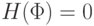 ,
то либо в
,
то либо в  нет отрицаний, либо все отрицания находятся
непосредственно перед переменными. Следовательно,
нет отрицаний, либо все отрицания находятся
непосредственно перед переменными. Следовательно,  удовлетворяет требованию
предложения 4.2.
удовлетворяет требованию
предложения 4.2.
Шаг индукции. Предположим, что при n <= k для всех
формул высоты n Предложение 4.2 выполнено.
Пусть  - произвольная формула высоты
- произвольная формула высоты  . Докажем
наше утверждение для нее. Поскольку
. Докажем
наше утверждение для нее. Поскольку  , то
, то  содержит хотя бы одну отрицательную подформулу
содержит хотя бы одну отрицательную подформулу  , у которой
, у которой  и, следовательно,
и, следовательно,  .
К такой формуле обязательно можно применить либо снятие двойного отрицания (4),
либо один из законов де Моргана (5). ( Объясните почему.)
Пусть
.
К такой формуле обязательно можно применить либо снятие двойного отрицания (4),
либо один из законов де Моргана (5). ( Объясните почему.)
Пусть  - это та подформула
- это та подформула  которая
на (2)-ом этапе процедуры первой заменяется на эквивалентную формулу
которая
на (2)-ом этапе процедуры первой заменяется на эквивалентную формулу  в соответствии с одной из указанных эквивалентностей.
Пусть
в соответствии с одной из указанных эквивалентностей.
Пусть 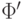 - это формула, получившаяся в результате этой
замены из
- это формула, получившаяся в результате этой
замены из  Нетрудно проверить (проделайте эту проверку!),
что при любом из преобразований (4), (5)
Нетрудно проверить (проделайте эту проверку!),
что при любом из преобразований (4), (5)  и, следовательно,
и, следовательно,  . Тогда
. Тогда  и по предположению индукции применение
эквивалентностей (4), (5) в произвольном порядке приведет в конце концов к
формуле, у которой все отрицания будут стоять непосредственно перед
переменными. Тем самым, предложение 4.2 выполнено
при n=k+1, что завершает индукционный шаг и все доказательство.
и по предположению индукции применение
эквивалентностей (4), (5) в произвольном порядке приведет в конце концов к
формуле, у которой все отрицания будут стоять непосредственно перед
переменными. Тем самым, предложение 4.2 выполнено
при n=k+1, что завершает индукционный шаг и все доказательство.
Рассмотрим применение процедуры приведения к совершенной ДНФ на примере.
Пример 4.1. Пусть формула 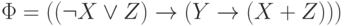 .
.
На (1)-ом этапе процедуры получаем следующую цепочку эквивалентностей:
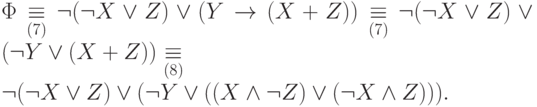
На (2)-ом этапе вносим отрицание внутрь первой скобки и получаем формулу
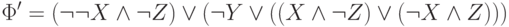
Устранив двойное отрицание, получим
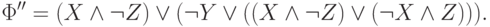
Нетрудно видеть, что это уже ДНФ. Удалим на (4)-ом этапе повторное вхождение первой конънкции и получим ДНФ
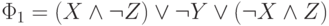
Эта ДНФ не является совершенной, так как в каждую из ее трех конъюнкций входят не все переменные. Построим на этапе (5) для них эквивалентные совершенные ДНФ (используя решение задачи 4.5).
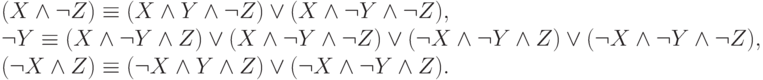
Подставив эти формулы в 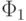 и устранив повторения конъюнкций,
получим совершенную ДНФ, эквивалентную исходной формуле
и устранив повторения конъюнкций,
получим совершенную ДНФ, эквивалентную исходной формуле 
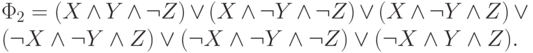
Мы видим, что ДНФ 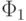 , полученная после 4-го этапа,
выглядит существенно проще, т.е. является более короткой, чем совершенная ДНФ
, полученная после 4-го этапа,
выглядит существенно проще, т.е. является более короткой, чем совершенная ДНФ  .
Однако совершенные ДНФ и КНФ обладают важным свойством единственности,
которое следует из их конструкции в теореме 4.1.
.
Однако совершенные ДНФ и КНФ обладают важным свойством единственности,
которое следует из их конструкции в теореме 4.1.
Следствие 4.1.2. Для каждой булевой функции от n переменных, не равной тождественно 0, существует единственная с точностью до перестановки конъюнкций и переменных внутри конъюнкций совершенная ДНФ, задающая эту функцию.
Это следствие позволяет предложить следующую процедуру для проверки эквивалентности формул  и
и 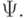
- Построить для
 и
и  эквивалентные совершенные
ДНФ
эквивалентные совершенные
ДНФ 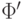 и
и  используя
процедуру приведения к совершенной ДНФ.
используя
процедуру приведения к совершенной ДНФ. - Упорядочить в соответствии с нумерацией
переменных X вхождения переменных в каждую
конъюнкцию, а затем лексикографически упорядочить между собой конъюнкции,
входящие в
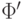 и
и  . Пусть в
результате получатся совершенные ДНФ
. Пусть в
результате получатся совершенные ДНФ  и
и 
- Если
 , то выдать ответ "Да", иначе - ответ "Нет".
, то выдать ответ "Да", иначе - ответ "Нет".
Замечание. Аналогичную процедуру можно построить с использованием совершенных КНФ.

 сама уже является
сама уже является